Risk Capital Attribution and Risk-adjusted Performance Measurement

After completing this reading, you should be able to:

• Define, compare, and contrast risk capital, economic capital, and regulatory capital, and explain methods and motivations for using economic capital approaches to allocate risk capital.
• Describe the RAROC (risk-adjusted return on capital) methodology and its use in capital budgeting.
• Compute and interpret the RAROC for a project, loan, or loan portfolio and use RAROC to compare business unit performance.
• Explain challenges that arise when using RAROC for performance measurement, including choosing a time horizon, measuring default probability, and choosing a confidence level.
• Calculate the hurdle rate and apply this rate in making business decisions using RAROC.
• Compute the adjusted RAROC for a project to determine its viability.
• Explain challenges in modeling diversification benefits, including aggregating a firm’s risk capital and allocating economic capital to different business lines.
• Explain best practices in implementing an approach that uses RAROC to allocate economic capital.

What is the Purpose of Risk Capital?

Risk capital acts as a cushion against the various risks a business takes. It takes the full brunt of the effects of taking risks, including misjudgments, adverse results, and outright losses. It serves two main purposes:

1. It helps businesses retain their financial integrity and status as a going concern even in the face of a near-catastrophic event.
2. It instills confidence among stakeholders such as lenders, suppliers, customers, and supervisory/regulatory authorities.

Risk capital is particularly important in the banking sector. Lenders who rely on customer deposits to fund loans and other investments must project financial integrity and financial stability to instill confidence among depositors. Even the slightest of rumors about financial turmoil can trigger a run, exposing a bank to serious liquidity problems.

In banking, risk capital is usually called economic capital, but as we shall see later in the chapter, risk capital is actually part of economic capital:

$$ \text{Economic capital = Risk capital + Strategic capital} $$

Economic Capital vs. Regulatory Capital

Economic capital is an institution’s own capital estimate of the amount it needs to remain solvent and maintain its day-to-day operations. Regulatory capital is the minimum amount of capital an institution is required to hold in accordance with bank regulators.

Every organization has to contend with economic capital. Regulatory capital, however, only comes up in instances where the regulatory authority in a given industry stipulates across-the-board standard capital requirements that all participants in the industry must comply with. In this regard, banks and insurance companies are subject to regulatory capital in all geographical jurisdictions around the world. It is important to note that regulatory capital specifies the minimum required level of capital adequacy and, therefore, may not capture the true level of risk in a firm.

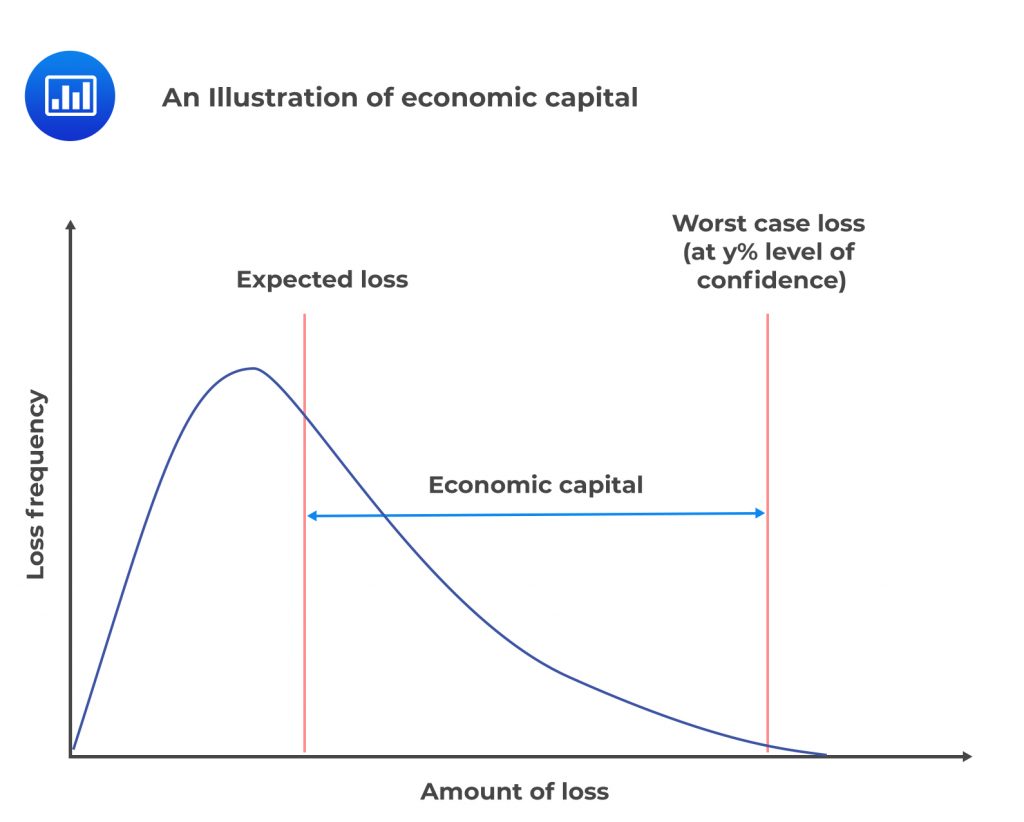Comparisons With VaR

A firm cannot offer its stakeholders a 100% guarantee that it holds enough risk capital to cushion itself from the entire universe of eventualities. What happens is that risk capital is calculated at a level of confidence less than 100%. If the one-year risk capital calculated at 99.9% confidence is Y, it means that over the next year, there’s only a 0.1% chance that actual losses will exceed Y. Firms settle upon a given level of confidence depending on the credit rating targeted from rating agencies such as Moody’s and Standard and Poors. The higher the desired credit rating, the higher the confidence level used.

How are Risk Capital Numbers Used?

Traditionally, risk capital has been used as an indicator of the amount of capital a firm requires to remain solvent, given its portfolio of risky investments. In recent times, however, more uses have come up. These include:

1. Evaluating performance and incentive compensation at the firm level, business unit level as well as individual level: This is achieved by using performance indicators, such as RAROC (risk-adjusted return on capital), that take risk capital into account.
2. Active portfolio management for entry/exit decisions: Any decision to enter or exit a particular business should consider both diversification and risk-adjusted-performance. Whenever a firm is faced with an entry/exit decision, it should consider how either decision will impact its risk capital.
3. Pricing transactions: Risk capital numbers can be used to come up with risk-adjusted prices of transactions to ensure that a firm is adequately compensated for taking risks.

Motivations for Using Economic Capital Approaches to Allocate Risk Capital

Financial institutions use capital not just as a source of funding for their investments but also as a risk absorber. Unlike nonfinancial institutions, financial institutions can take on large amounts of leverage at low costs. They can, for example, do so by simply accepting customer deposits or issuing a bond. It is not unusual to find a bank with a debt-to-equity ratio of 20 or more. It is noteworthy, however, that nonfinancial institutions rarely venture above 2. On the same note, financial institutions engage in a wide range of transactions, such as derivatives trading, writing guarantees, and FX trading, that do not require significant financing. But all of these activities draw on an institution’s risk capital. Therefore, a risk capital cost must be included in each activity.

Financial institutions have to demonstrate creditworthiness. For financial institutions, their customers double up as their creditors. That means customers are always monitoring the financial health of their bank. Customers make their deposits with the expectation that the safety of their deposits is not hinged on the bank’s economic performance in any way. Any signs of trouble can trigger a run, leaving a bank short of funds. For this reason, the bank is incentivized to maintain creditworthiness at all times.

Banks are traditionally opaque institutions with complex books. They engage in complex transactions that often use proprietary technology that ordinary stakeholders cannot scrutinize. In addition, the balance sheet position of a bank can change pretty fast, with liquidity being wiped out or even restored in a matter of hours or days. That means accounting analysis becomes obsolete quite fast. For these reasons, banks are incentivized to maintain adequate risk capital and implement robust risk management frameworks to reduce agency costs. Such initiatives will convince all stakeholders that banks’ financial integrity is beyond reproach and that there’s no cause for concern.

A bank’s profitability is highly sensitive to its cost of capital. On the one hand, a bank cannot hold too much capital since that stifles profitability, considering that a bank can only invest risk capital in safe, low-yield assets. On the other hand, a bank cannot afford to hold risk capital that’s too little since this raises the specter of insolvency. As such, it is important that a bank strikes a balance between holding sufficient economic capital and the uptake of risky but positive NPV projects.

Risk-adjusted Return on Capital (RAROC)

Risk-adjusted return on capital (RAROC) is a metric used to determine the return on investment, taking full cognizance of risk elements. It expresses the expected after-tax profit as a percentage of economic capital.

$$ \text{RAROC} =\cfrac { \text{After-tax risk-adjusted net income} } { \text{Economic capital} } $$

RAROC offers a uniform and comparable measure of risk-adjusted performance across all business units. A business unit is deemed to add value to shareholders only if its RAROC is higher than the cost of equity. The cost of equity can be calculated according to the capital asset pricing model.

How is RAROC Important?

1. It helps banks to single out deals that may appear highly profitable on paper but actually have more than a commensurate capital requirement. In other words, it exposes seemingly profitable but excessively risky deals. In the same vein, RAROC helps draw attention to deals that offer a high risk-adjusted return even though they have a deceptively low gross return.
2. As a forward-looking measure, it discourages short-term optimization of sales volume at the expense of large losses in the future.
3. It takes economic profits rather than accounting profits which include historical, arbitrary, and subjective values, such as depreciation.
4. It is exhaustive and flexible: Exhaustive in the sense that it considers all financial variables such as sales, expenses, and capital. It is flexible because it can be computed at the firm level or refined to the level of individual business lines, branches, or deals.

Computing and Interpreting the RAROC

For purposes of capital budgeting, a more detailed RAROC equation is used:

$$ \text{RAROC} = \cfrac { \text{Expected revenues-Costs-Expected losses-Taxes+} \\ \text{Return on risk capital+/- Transfers}}{ \text{Economic capital} } $$

Where:

• • Expected revenues are the revenues that the activity is expected to generate (assuming no losses).
  • Costs are the direct expenses associated with running the activity (e.g., salaries, bonuses, infrastructure expenses, and so on).
  • Expected losses (EL) consist mainly of expected default losses (i.e., loan loss reserve). Expected losses also include the expected loss from other risks, such as market risk and operational risk.
  • Taxes are the expected amount of taxes imputed to the activity using a company’s effective tax rate.
  • Return on economic capital refers to the return on risk-free investments (government bonds) based on the amount of allocated risk capital.
  • Transfers correspond to costs associated with upstream or downstream transactions between a business unit and the central treasury group, e.g., funding costs and overhead allocations. It also includes the cost of hedging interest rates and currency risks.
  • Economic capital is the sum of risk capital and strategic risk capital. Strategic risk capital refers to the risk associated with large, potentially highly profitable investments whose success is, however, shrouded in uncertainty. The failure of a strategic investment could result in a major write-off and reputational damage. Strategic risk capital is the sum of goodwill and burned-out capital.
    • Goodwill is the excess of the purchase price over the replacement value (fair value) of the net assets recorded on the balance sheet. It represents an investment premium that recognizes the value of intangible assets, such as a good brand name, an outstanding and loyal workforce, patents, and proprietary technology. It is usually recognized when a firm acquires another firm. Goodwill is not depreciated like other assets. Instead, it is regularly tested for impairment.
    • Burned-out capital represents the risk of funds spent during the start-up phase of a venture that may be lost in case the projected risk-adjusted returns are deemed too low, forcing a firm to abandon the venture altogether. The venture could be a new investment project developed internally. Besides, it could also be a recent merger or acquisition. Burned-out capital is gradually amortized as the risk of failure decreases.

Some banks also allocate risk capital for unused risk limits (undrawn amounts on lines of credit) because there’s always a chance that the extra risk capacity will be tapped at some point. If a bank taps the extra risk capacity, it would have to adjust its risk capital upwards.

Important: We must bear in mind that economic capital is a cushion against unexpected losses at a given level of confidence. The difference between the worst-case loss and the expected loss gives the unexpected loss. For example, let’s assume that in a given transaction, the expected loss and the worst-case loss at 99% confidence are 50 basis points and 150 basis points, respectively. In this case, the unexpected loss is 100 basis points over the relevant horizon, usually one year. The unexpected loss corresponds to the risk of capital allocated to the transaction.

Example: Computing and Interpreting the RAROC

A bank in the U.S. is considering building a portfolio of corporate loans with the following characteristics:

• Principal amount: $10 billion.
• Headline (pre-tax expected) return: 7%.
• Operating direct costs: 1% of the principal amount.
• The portfolio is funded by $10 billion of retail deposits that attract an interest charge of 4%.
• Chief Risk Officer projects an expected loss of 1% and a worst-case loss of 7% of the principal amount per annum.
• The risk-free rate of interest: 3%.
• Effective tax rate: 30%.
• Transfers: $0.

Compute the risk-adjusted return on capital.

Solution

As a first step, we have to work out all the values we need:

$$ \text{RAROC} = \cfrac { \text{Expected revenues}-\text{Costs-Expected losses-Taxes}+ \\ \text{Return on risk capital+/- Transfers}}{ \text{Economic capital} } $$

Expected revenues = 7% × $10 billion = $700 million.

Costs = operating cost + interest charge = (1% + 4%)$10 billion = $500 million.

Expected loss = 1% × $10 billion = $100 million.

Economic capital = unexpected loss = worst case loss – expected loss = (7% – 1%)$10 billion = $600 million.

Return on risk capital = $600 million × 3% = $18 million.

Therefore,

$$ \text{RAROC} = \cfrac { \left(700-500-100+18+0 \right) \left(1-0.3 \right)}{600} =13.77\% $$

Interpretation: The annual after-tax expected rate of return on equity needed to support this portfolio is 13.77%.

Note: Since the analysis is being performed ex-ante, we should use expected revenues and losses in the numerator. We would have to use realized revenues and losses to analyze portfolio performance on an ex-post basis.

RAROC Horizon

When calculating RAROC, practitioners usually adopt a one-year time horizon since this aligns with the business planning cycle and also presents a reasonable approximation of the amount of time that would be needed to recapitalize if a firm were to suffer a major unexpected loss. However, looking at multi-period RAROC spanning as many as five years is also possible. This would help a firm to estimate the economic capital needed for longer-term transactions.

Notably, calculating economic capital over a longer horizon may not result in a significant increase in capital because the confidence level in any firm’s solvency decreases as the time horizon increases. In the same vein, the quality and accuracy of risk and return data decline as we peer further into the future.

Risk capital can also be viewed as the one-year VaR at a confidence level that reflects a firm’s target credit risk rating. For credit risk measured using models such as the CreditMetrics and KMV that assume a one-year horizon, the one-year VaR is equivalent to risk capital. Similarly, the one-year VaR with respect to operational risk is equivalent to the one-year risk capital. But when it comes to market risk, some adjustment is needed.

Due to the nature of markets to move significantly over short-term periods, market risk is measured using only short-term horizons – one day for risk monitoring, and 10 days for regulatory capital. As such, we have to adjust the one-day or ten-day VaR into an annual figure so as to determine the one-year capital allocation. The most common approach used to scale up the VaR to an annual value involves the use of the square root of time rule:

$$ \text{One-year VaR} = \text{One-day VaR} × \sqrt{\text{Number of business days in a year}} $$

For purposes of risk capital determination, the use of the square root of time rule needs to be fine-tuned because of two main reasons:

1. Risk capital is meant to help a firm overcome a period of stress occasioned by a major loss. Even in a worst-case scenario, a firm might only be able to reduce its risk to a core risk level that guarantees it retains its status as a financially viable business for the rest of the year.
2. There’s a need to factor in the time needed to scale down the current risk level to the core risk level. A firm will need some time to liquidate its investment positions accordingly.

Example: Required Risk Capital as a Percentage of Annualized VaR

A bank’s core risk level is below the current risk position. The following information is provided:

• Daily VaR: 100.
• Core risk level: 80.
• Days needed to reduce current risk level to core risk level = 10 (i.e., a reduction of 2 VaR per day).

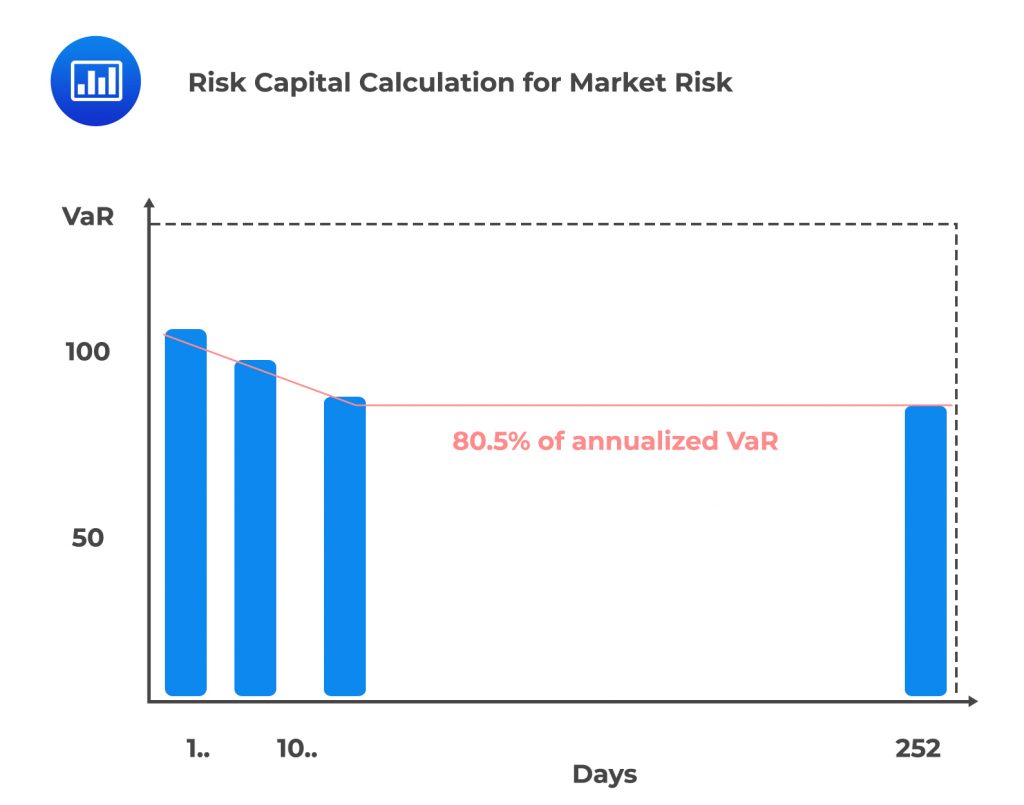
Assuming that there are 252 business days in a year, compute the required risk capital as a percentage of annualized VaR.

Solution

$$ \begin{align*} \text{Risk capital} &= \\ &\sqrt { \left\{ \text{sum of squares+ } \\ \text{core risk level squared(business days per year-days needed to reduce current to core)} \right\} } \\ &=\sqrt{ {100}^{2} + {98}^{2} + {96}^{2} + {94}^{2} + {92}^{2} + {90}^{2} + {88}^{2} + {86}^{2} + {84}^{2} + {82}^{2} + {80}^{2} \times \left(252-10\right) } \\ &=\sqrt { 83,140+1,548,800 }=1,277.4741 \end{align*} $$

Now,

$$ \begin{align*} \text{One-year VaR} &= \text{one-day VaR} * \text{square root (number of business days in a year)} \\ &=100 \times \sqrt{252} =1,587.4508 \end{align*} $$

Therefore, the required risk capital is 80.5% of the annualized VaR (= 1,277.4741/1587.4508).

There are many more banking activities that must be allocated capital in a way that is sensitive to time horizons. In particular, a bank should allocate capital to cover the risk of options embedded in its products. A good example would be capital set aside to cover the option to prepay a mortgage.

Confidence Interval

As mentioned earlier, a firm’s economic capital calculation should be consistent with its target credit rating. In practice, banks often target an AA rating for their debt offerings, translating to a probability of default of 3 to 5 basis points. This, in turn, corresponds to a level of confidence in the range of 99.95 to 99.97 percent.

The choice of confidence level has a material impact, not just on risk-adjusted performance measures but also on the amount of capital allocated to an activity. The higher the confidence level, the higher the amount of risk capital allocation, and vice versa.

Default Probability

There are two stylized approaches used to model the probability of default: a point-in-time approach and a through-the-cycle approach.

1. A point-in-time (PIT) probability of default (PD) assesses the likelihood of default at a particular point in time. As it assesses risk at a point in time, a firm will move up or down rating grades through the economic cycle.
2. A through-the-cycle (TTC) probability of default (PD), in contrast, predicts the average default rate for a particular firm over an economic cycle. It ignores short-run changes to a firm’s PD and thus results in a stable rating grade through the economic cycle.

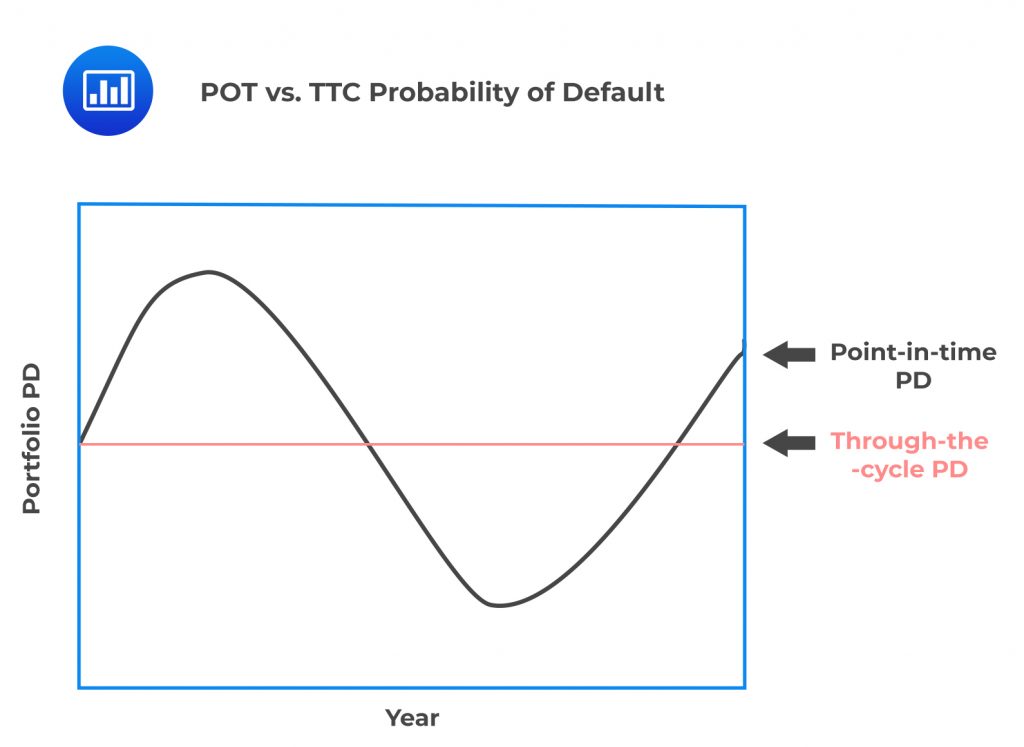Compared to the point-in-time approach, the through-the-cycle approach reduces the volatility of economic capital. Firms usually compare the impact of using the point-in-time probability of default versus the through-the-cycle probability of default in the RAROC calculation for both a normal part of the economic cycle and the worst part of the cycle.

Hurdle Rate and Capital Budgeting Decision Rule

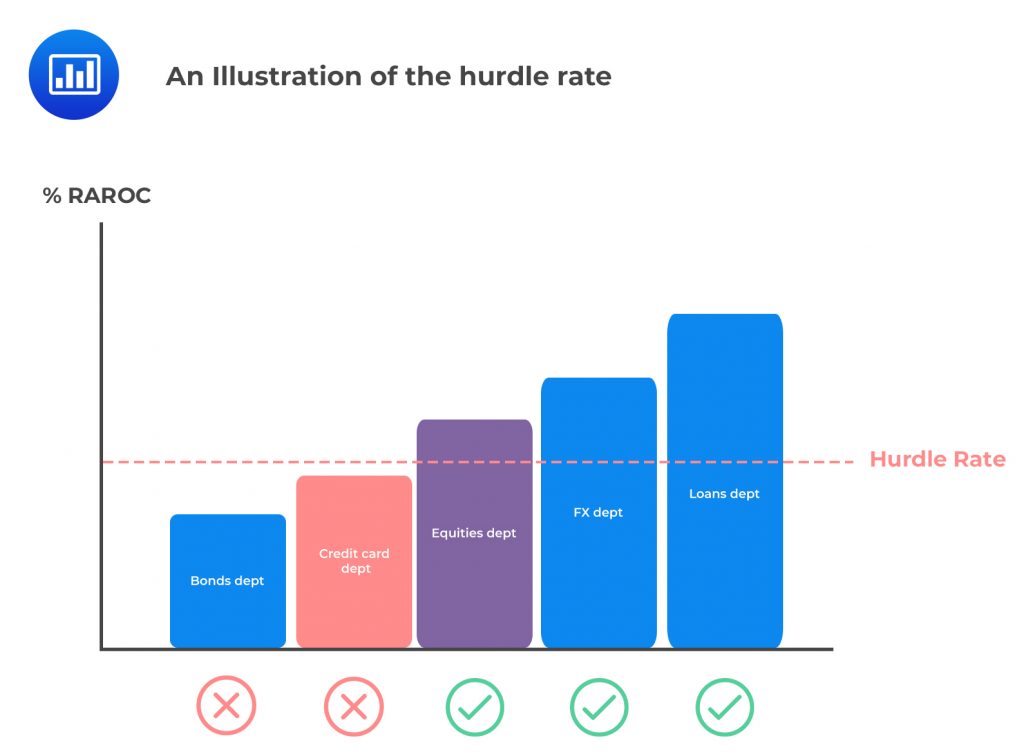
When a firm is considering venturing into a business or closing down one altogether, it computes the after-tax RAROC. The firm then compares the after-tax RAROC to its (firm’s) hurdle rate. A hurdle rate is the minimum required rate of return or target rate that investors are expecting to receive on an investment.

The firm then applies a simple decision rule:

• If the RAROC ratio is greater than the hurdle rate, the activity may be pursued because it is deemed to add value to the firm.
• If the RAROC ratio is less than the hurdle rate, the activity is rejected or terminated because it is deemed to destroy value for the firm.

The hurdle rate is computed as the after-tax weighted average of the cost of equity capital:

$$ \text{h}_{ \text{AT} }= \cfrac {{ \text{CE} } \times { \text{r}}_{ \text{CE} }+{ \text{PE} } \times { \text{r} }_{ \text{PE} } } {{ \text{CE} }+{ \text{PE} } } $$

Where:

• \({ \text{h} }_{ \text{AT} }\) = After-tax hurdle rate.
• CE and PE denote the market value of common equity and preferred equity, respectively.
• \({ \text{r} }_{ \text{CE} }\) and \({ \text{r} }_{ \text{PE} }\) are the cost of common equity and preferred equity, respectively.

The cost of preferred equity is taken to be the yield on a firm’s preferred shares. The cost of common equity is determined via the Capital Asset Pricing Model.

$$ { \text{R} }_{ \text{CE} }={ \text{R} }_{ \text{F} }+{ \beta}_{ \text{CE} } \left( { \text{R} }_{ \text{M} }-{ \text{R} }_{ \text{F} } \right) $$

where:

\({ \text{R} }_{ \text{CE} }\) = Cost of common equity.

\({ \text{R} }_{ \text{F} }\) = Risk free rate of interest.

\({ \beta}_{ \text{CE} }\) = Beta for the firm’s common equity.

\({ \text{R} }_{ \text{M} }\) = Expected return on the market portfolio.

Example: Computing the Cost of Equity Capital

$$ \begin{array}{l|c} \text{Beta of common equity} & {1.2} \\ \hline \text{Risk-free rate} & {5.0\%} \\ \hline \text{Expected market return} & {12.00\%} \\ \hline \text{Expected return on common equity} & {= 5.0 + 1.2 \left(12.0 – 5.0\right) = 13.4\%} \\ \hline {} & {} \\ \hline \text{Yield on preferred stock} & {8.0\%} \\ \hline {} & {} \\ \hline \text{Market value of common equity} & $ \text{100 million} \\ \hline \text{Market value of preferred equity} & $ \text{20 million} \\ \hline {} & {} \\ \hline \text{Cost of equity capital} & \text{ \( = \cfrac { \left(100 \times 13.4\% + 20 \times 8.0\% \right) } { \left(100 + 20 \right) } = 12.5\% \)} \\ \hline \text{Implication for any project or business unit} & \text{RAROC must be greater than 12.5%} \end{array} $$

The use of a hurdle rate comes with a challenge: The firm may end up accepting high-risk projects that will lower its value. At the same time, it might reject low-risk projects that will increase the value of the firm.

Adjusted RAROC

The adjusted RAROC (ARAROC) adjusts the traditional RAROC to take the systemic riskiness of returns into account and use a hurdle rate that remains the same across all business lines.

\( \text{Adjusted RAROC} = \text{RAROC} – { \beta }_{ \text{E} } \left({ \text{R} }_{ \text{M} }-{ \text{R} }_{ \text{F} } \right) \)

Where:

\({ \text{R} }_{ \text{F} }\) = Risk-free rate = hurdle rate.

\({ \beta }_{ \text{E} }\) = Firm’s equity beta.

\({ \text{R} }_{ \text{M} }\) = Expected return on market portfolio.

\({ \text{R} }_{ \text{M} }-{ \text{R} }_{ \text{F} } \) = Excess return over risk-free rate to account for the non-diversifiable systematic risk of the activity.

The revised decision rule is as follows:

• If the adjusted RAROC is greater than the risk-free rate, accept the project.
• If the adjusted RAROC is less than the risk-free rate, reject the project.

Example: Adjusted RAROC

$$ \begin{array}{l|c} \text{RAROC} & {10.0\%} \\ \hline \text{Risk-free rate} & {5.0\%} \\ \hline \text{Expected return on market portfolio} & {12.0\%} \\ \hline \text{firm’s equity beta} & {0.8} \\ \hline {} & {} \\ \hline \text{ARAROC} & {= 0.10 – 0.8(0.12 – 0.05) = 0.016 = 4.4\%} \\ \hline \text{Decision rule} & \text{Reject the project since ARAROC < \( {\text{R} }_{ \text{F} } \) } \end{array} $$

Challenges in Modeling Diversification Benefits

Aggregating a Firm’s Risk Capital

In order to determine the risk capital for a particular business unit within a larger firm, each unit is typically viewed on a stand-alone basis. However, finance theory tells us that there’s bound to be some diversification benefits when all the business units are viewed together. That’s because the correlation of returns is likely to be less than +1. As such, the risk capital for the firm should be significantly less than the sum of the stand-alone risk capital of individual business units.

Example: Aggregating a Firm’s Risk Capital

Assume that the complete array of risks facing a firm is as follows (all figures in millions):

• Market risk = $500.
• Credit risk = $400.
• Operational risk = $600.
• Liquidity risk = $300.

Case 1: Aggregate Risk Capital Assuming a Perfect Correlation

Risk capital is simply the sum of the four risk capital amounts:

Risk capital = $1,800.

Case 2: Aggregate Risk Capital Assuming Zero Correlation

Risk capital is given as the square root of the sum of squares of the four risk capital amounts:

Risk capital = \( \sqrt{ {500}^{2} + {400}^{2}+ {600}^{2}+ {300}^{2} } =$927 \)

As this example shows, the aggregate risk capital for the firm can be as high as $1,800 or as low as $927 – quite a wide range. Given this result, we would expect that any risk capital calculation process that takes diversification effects should yield an overall VaR figure in the range of 927 to $1,800.

Although, undoubtedly, there’s a diversification effect, measuring it is quite an uphill task. In fact, we do not have a model that can estimate the correlation between market risk, credit risk, and operational risk across all the business units with good enough accuracy. One way firms try to overcome this problem is by lowering the confidence level when measuring each individual risk so as to avoid an excessively high-risk capital amount.

Allocating Economic Capital to Different Business Lines

Measuring the exact amount of the diversification benefit is not the only problem. Firms have to find a way to allocate the aggregate diversification benefit to specific business units. Allocating the diversification benefit can help in decision-making, e.g., when deciding which business line to terminate, scale up, or down.

It is logical to allocate more risk capital to a business unit whose earnings correlate highly to the overall firm. But firms struggle to come up with a precise method of doing this, and most settle for a pro-rata allocation approach based on stand-alone risk capital amounts.

Example: Allocating economic capital to different business lines

Assume that we have a business unit that engages exclusively in two activities – X and Y.

Further, assume that:

• Activity X alone requires $80 of risk capital.
• Activity Y alone requires $70 of risk capital.
• Activities X and Y combined require a total of $110 of risk capital.

Case 1: Stand-alone Capital

If we ignore any diversification benefits, activities X and Y will have stand-alone capital of $80 and $70, respectively. In addition, the stand-alone capital for the business unit is $110.

Case 2: Fully Diversified Capital

The diversification benefit is $40 (= 150 – 110).

We can attribute this to each of the two activities on a pro-rata basis as follows:

• Allocation of diversification benefit to activity X = 80/150 × 40 = 21.33.
• Allocation of diversification benefit to activity Y = 70/150 × 40 = 18.67.

Therefore, X and Y will have a fully diversified capital of $58.67 (= 80 – 21.33) and $51.33 (= 70 – 18.67).

Case 3: Marginal Capital

Marginal capital is the additional capital an incremental deal, activity, or business requires. It takes the full benefit of diversification into account. In our case,

• Marginal risk capital for X (assuming that Y already exists) is $40 (= $110 total – $70 for Y).
• Marginal risk capital for Y (assuming that X already exists) is $30 (= $110 total – $80 for X).

Generally, the marginal risk capital of a business unit X is calculated as the risk capital required for the unit minus the risk capital required for the full portfolio of businesses.

Important Points:

• Fully diversified measures should be used for assessing the solvency of the firm and minimum risk pricing.
• Decisions to do with active portfolio management or the appropriate business mix should be based on marginal risk capital, taking into account the benefit of full diversification.
• Finally, performance measurement should involve both perspectives: stand-alone risk capital for incentive compensation and fully diversified risk capital to assess the extra performance attributable to diversification.

The issue of diversification and its effect on risk capital needs to be approached with a certain level of caution because correlations can change dramatically over time. For example, during a financial crisis or severe period of stress, correlations tend to shift toward 1 or -1. This reduces or even totally eliminates the diversification effect for some time.

Best Practices in Implementing an Approach That Uses RAROC To Allocate Economic Capital

There are a number of recommendations for firms that intend to implement a RAROC approach to the allocation of economic capital:

• Let the senior management take charge of the entire process, emphasizing the importance of making sure that the firm is adequately compensated for every risk taken.
• Firm-wide education to ensure that everyone understands what RaROC is all about and the role they have to play.
• Regular review of key parameters by a review group to ensure that they reflect current trends.
• Data quality should be safeguarded to maintain the integrity of the process and results.
• A firm should combine RAROC with qualitative considerations such as the strategic importance of a project, growth potential, legal aspects, etc.
• There should be active capital management, where capital demands and requests are well documented and compliance with in-house limits enforced.

Practice Question

We have been given the following information for a project:

• Expected revenue: USD 75 million.
• Return on risk capital: USD 21 million.
• Economic capital: USD 73 million.
• Tax expense: USD 22 million.
• Operating cost: USD 8 million.
• Expected loss: USD 5 million.

What is the RAROC for the project?

A. 0.2627.

B. 0.8356.

C. 0.9726.

D. 1.0548.

The correct answer is B.

Recall that:

$$ \text{RAROC} = \cfrac { \text{expected revenues-costs-expected losses-taxes+} \\ \text{return on risk capital+/- transfers}}{ \text{economic capital} } $$

Therefore:

$$\begin{align*} RAROC&=\frac { 75-8-22-5+21 }{ 73 }\\ &=0.8356 \end{align*}$$