Credit Scoring and Retail Credit Risk ...
After completing this reading, you should be able to: Analyze the credit risks... Read More
After completing this reading, you should be able to:
Empirical evidence has shown that high-beta stocks underperform low-beta stocks on a risk-adjusted basis. This has led to managers following strategies meant to exploit these anomalous patterns. This situation is referred to as a low-risk anomaly since it contradicts the capital asset pricing model (CAPM), which suggests that there is a positive relationship between risks and returns and that higher risk, or higher beta, implies higher returns.
Alpha is the average return in excess of a market index or a benchmark. Therefore, a benchmark against which alpha is measured has to be defined.
Excess return or active return, \({ \text{r} }_{ \text{t} }^{ \text{ex} }\), is defined as the return of an asset or a strategy in excess of a benchmark, that is:
$$ \begin{align*} { \text{r} }_{ \text{t} }^{ \text{ex} }={ \text{r} }_{ \text{t} }-{ \text{r} }_{ \text{t} }^{ \text{bmk} } \end{align*} $$
Where:
Alpha is then computed by taking the average of the active returns:
$$ \begin{align*} \alpha =\cfrac { 1 }{ \text{T} } \sum _{\text{t}=1 }^{ \text{T} }{ { \text{r} }_{ \text{t} }^{ \text{ex} } } , \end{align*} $$
Where \(T\) represents the number of observations in the sample.
Tracking error identifies the level of consistency in which a portfolio follows the performance of the benchmark. A low tracking risk implies that the portfolio is closely following the benchmark. A high tracking error implies that the portfolio is volatile relative to the benchmark and that returns are moving away from the benchmark.
$$ \begin{align*} \text{Tracking error} \left(\text{TE}\right)=\text{S}\left(\text{r}_\text{t}^\text{ex}\right) \end{align*} $$
Where \(S\) is the sample standard deviation.
The information ratio (IR) is a measure of returns of a portfolio above the returns of a benchmark in comparison to the returns’ volatility. The benchmark is typically an index representing the market or a particular sector. The IR is used as a measure of a portfolio manager’s skills and ability to generate excess returns relative to the benchmark. It also identifies the consistency of the performance by incorporating a tracking risk component into the calculation.
The information ratio standardizes the returns by dividing the difference in their performances by their tracking risk.
$$ \text{IR} = \cfrac{\alpha}{\text{TE}} $$
The Sharpe ratio is a special case of IR when the benchmark is the risk-free rate, \({\text{r}}_{\text{t}}^{\text{f}}\).
Alpha is, therefore, the average return over the risk-free rate, \({\alpha}= \overline{ { \text{r} }_{ \text{t} }-{ \text{r} }_{ \text{t} }^{ \text{f} } } \).
The Sharpe ratio is, thus, given by:
$$ \text{SR}=\frac { \overline { { r }_{ t }-{ r }_{ ft } } }{ \sigma } $$.
Where \(\sigma\) represents the standard deviation of the portfolio.
Performance is mainly defined using returns and alphas. Lehmann and Modest showed that a benchmark choice could critically impact the estimate of alpha.
Martingale, in his case study, based his low volatility strategy on the Russell 1000 universe of large stocks. Russell 1000, or any other identifiable index, may be a natural choice for a benchmark with an asset beta of 1.0. However, the true beta could be a different value, say 0.73, like in the case of Martingale’s product. Regression on the excess returns of the fund relative to T-bills (risk-free asset) on excess returns of the Russell 1000 was run to obtain:
$$ \text{R}_\text{t}-\text{R}_\text{f}=0.0344+0.7272\left(\text{R}_\text{r1000}-\text{R}_\text{f} \right)+{ \varepsilon }_{ \text{t} } $$
Where:
Rearranging the above equation, we obtain:
$$ \text{R}_\text{t}=0.0344+0.2728\text{R}_\text{f}+0.7272{\text{R}}_{\text{R}1000}+{ \varepsilon }_{ \text{t} } $$
The above equation implies that Martingale’s low-volatility strategy outperforms the benchmark by 3.44% per year (alpha of 3.44%).
Suppose one uses a naive benchmark of Russel 1000, with a beta of 1.0 instead, we would have:
$$ \text{R}_\text{t}=0.015+\text R_{\text R 1000}+{ \varepsilon }_{ \text{t} } $$
So that the alpha is 1.5% per year. This implies a reduced performance of approximately 1.9%. Therefore, a different choice of benchmark affects the alpha estimate.
The following are the features of an ideal benchmark for measuring alpha:
By making bets deviating from a benchmark, a portfolio manager creates alpha in comparison to the benchmark. Successful bets typically imply a higher alpha. In 1989, Richard Grinold formulated the fundamental law of active management, which formalizes this intuition. The fundamental law states that the maximum information ratio attainable is given by:
$$ \begin{align*} \text{IR}=\text{IC}\times\sqrt { \text{BR} } \end{align*} $$
Where:
The information coefficient is simply a measure of how good a manager’s forecasts are, relative to the actual returns. The breadth of the strategy, on the other hand, represents the number of bets taken. Breadth refers to the number of securities that can be traded and the frequency of trading them. In 1999, Grinold and Kahn emphasized the importance of playing often and well. That is, a high BR and a high IC.
The following are the assumptions of Grinold’s fundamental law and its limitations:
Consider the CAPM formula:
$$ \begin{align*} \text{E}\left({\text{R}}_{\text{i}}\right)-{\text{R}}_{\text{f}}={\beta }_{\text{i}} \left({\text{E}}\left({\text{R}}_{\text{m}} \right)-{\text{R}}_{\text{f}}\right) \end{align*} $$
Where:
Suppose \({\beta }_{\text{i}}\)=1.6, so that the above equation becomes:
$$ \begin{align*} \text{E}\left({\text{R}}_{\text{i}}\right) & ={\text{R}}_{\text{f}}+1.6\text{E}\left({\text{R}}_{\text{m}} \right)-1.6{\text{R}}_{\text{f}} \\ \Rightarrow \text{E}\left({\text{R}}_{\text{i}}\right) & =-0.6{\text{R}}_{\text{f}}+1.6\text{E}\left({\text{R}}_{\text{m}} \right) \end{align*} $$
In this case, CAPM assumes that the same return as $1 in asset \(i\) can be produced by holding a short position in a risk-free portfolio of $0.60 and an extended position of $1.60 in the market portfolio. Joining risk-free assets and the market obtains the same expected return as the asset when using the CAPM. This implies that the beta of the asset is mimicking portfolio weight and, therefore, the CAPM implies a replicating portfolio.
The alpha of an asset \(i\) is any expected return generated in excess of the short $0.60 in the risk-free rate portfolio and the long $1.60 position in the market portfolio:
$$ \text{E}\left({\text{R}}_{\text{i}}\right)={\alpha}_{\text{i}}+\left[-0.6{\text{R}}_{\text{f}}+1.6\text{E}\left({\text{R}}_{\text{m}} \right)\right] $$
Where the benchmark comprises the risk-adjusted amount held in equities and the risk-free rate, \({\text{R}}_{\text{bmk}} = -0.6{\text{R}}_{\text{f}}+1.6{\text{R}}_{\text{m}}.\)
As observed in the above discussion, factor regressions can be applied in the estimation of the risk-adjusted benchmark, or equivalently the mimicking portfolio.
Alpha is obtained by performing regression analysis:
$$ \begin{align*} {\text{R}}_{\text{it}}-{\text{R}}_{\text{ft}}={\alpha}+{\beta}_{\text{i}} ({\text{R}}_{\text{mt}}-{\text{R}}_{\text{ft}} )+{ \varepsilon }_{\text{it}} \end{align*} $$
Where the residuals \(\varepsilon_{\text{it}}\) are independent of the market factor.
A CAPM regression on the above equation was run on the monthly returns on Berkshire Hathaway for the period ranging from January 1990 to May 2012 to yield CAPM-implied mimicking portfolio weights. The estimates are shown in the table below:
$$ \begin{align*} \begin{array}{l|c|c} {} & \textbf{Coefficient} & \textbf{t-statistic} \\ \hline \text{Alpha} & \text{0.72%} & {2.02} \\ \hline \textbf{Beta} & {0.51} & {6.51} \\ \hline \text{Adjusted \({\textbf{R}}^{2}\)} & {0.14} & {} \end{array} \end{align*} $$
This implies that the CAPM benchmark constitutes \(1-51%=49%\) invested in the risk-free asset and \(51%\) invested in the market portfolio; that is:
$$ \begin{align*} {\text{R}}_{\text{bmk}} = 0.49{\text{R}}_{\text{f}}+0.51{\text{R}}_{\text{m}} \end{align*} $$
Alpha is 0.72% per month and, therefore, the alpha generated per year is \(0.0072×12 = 8.6\%\), with a risk of approximately half that of the market \(\left({\beta}=0.51\right)\).
The alpha has a high t-statistic of the above two, which shows that it is statistically significant. The cutoff level of two corresponds to the 95% confidence level.
The adjusted \({\text{R}}^{2}\) of the CAPM regression is also relatively high at 14%. For most stocks, CAPM regressions produce adjusted \({\text{R}}^{2}\)’s of less than 10%. The high \({\text{R}}^{2}\) implies that the fit of the CAPM benchmark is very well relative to the typical fit of a CAPM regression for an individual stock.
In 1993, Eugene Fama and Kenneth French introduced a benchmark by extending CAPM to include factors capturing a size effect and value-growth effect. These factors were labeled SMB and HML, for “Small stocks Minus Big stocks” and “High book-to-market stocks Minus Low book-to-market stocks.”
These two factors, HML and SMB, are long-short factors. They mimic portfolios made up of simultaneous $1 long and $1 short positions in different stocks:
$$ \begin{align*} \text{SMB}&=$1 \text{ in small caps }-$1 \text{ in large caps } ; \text{and} \\ \text{HML}&=$1 \text{ in value stocks }-$1 \text{ in growth stocks } \end{align*} $$
This benchmark holds positions in the SMB and HML factor portfolios alongside a position in the market portfolio like in the traditional CAPM. The following regression is run to estimate the Fama-French benchmark:
$$ \begin{align*} {\text{R}}_{\text{it}}-{\text{R}}_{\text{ft}}={\alpha}+{\beta}_{{\text{i}},{\text{MKT}}} \left({\text{R}}_{\text{mt}}-{\text{R}}_{\text{ft}} \right)+{\beta}_{{\text{i}},{\text{SMB}}} {\text{SMB}}_{\text{t}}+{\beta}_{{\text{i}},{\text{HML}}} {\text{HML}}_{\text{t}}+{{ \varepsilon }}_{\text{it}}, \end{align*} $$
The assumption always when running factor regression is that a factor benchmark portfolio can be created.
The estimates for the Fama-French regression for Berkshire Hathaway yield the coefficients shown in the table below:
$$ \begin{align*} \begin{array}{c|c|c} {} & \textbf{Coefficient} & \textbf{t-statistic} \\ \hline \text{Alpha} & {0.65\%} & {1.96} \\ \hline \text{MKT Loading} & {0.67} & {8.94} \\ \hline \text{SMB Loading} & {-0.50} & {-4.92} \\ \hline \text{HML Loading} & {0.38} & {3.52} \\ \hline \text{Adjusted \({\textbf{R}^{2}}\)} & {0.27} & {} \end{array} \end{align*} $$
It can be observed that, as a result of controlling for size and value, alpha has reduced from 8.6% to 7.8% (0.65%×12). The market beta has also increased from 0.51 to 0.67. Generally, we obtain the benchmark as shown below:
(1 – 0.67) = $0.33 in risk-free portfolio + $0.67 in the market portfolio − $0.50 in small caps + $0.50 in large caps + $0.38 in value stocks − $0.38 in growth stocks.
Berkshire is adding 0.65% (alpha) relative to the above benchmark.
The momentum effect can be added to the factor benchmark. Momentum is a systematic factor observed in most asset classes. A momentum factor, WML (Winning stocks Minus Losing stocks) is added to the Fama-French benchmark:
$$ { \text{r} }_{ \text{it} }-{ \text{r} }_{ \text{ft} }=\alpha +{ \beta }_{ \text{i,MKT} }\left( { \text{R} }_{ \text{mt} }-{ \text{R} }_{ \text{ft} } \right) +{ \beta }_{ \text{i,SMB} }{ \text{SMB} }_{ \text{t} }+{ \beta }_{ \text{i,HML} }+{ \text{HML} }_{ \text{t} }+{ \beta }_{ \text{i,WMl} }{ \text{WML} }_{ \text{t} } +{ \varepsilon }_{ \text{it} } $$
The estimates for the extended Fama-French regression for Berkshire Hathaway yield the coefficients shown in the table below:
$$ \begin{array}{l|c|c} {} & \textbf{Coefficient} & \textbf{t-statistic} \\ \hline \text{Alpha} & {0.68\%} & {2.05} \\ \hline \text{MKT Loading} & {0.66} & {8.26} \\ \hline \text{SMB Loading} & {-0.50} & {-4.86} \\ \hline \text{HML Loading} & {0.36} & {3.33} \\ \hline \text{WML Loading} & {-0.04} & {-0.66} \\ \hline \text{Adjusted \({\textbf{R}^{2}}\)} & {0.27} & {} \end{array} $$
The mimicking portfolio implied by the extended Fama-French benchmark is:
(1–0.66) = $0.37 in risk-free portfolio + $0.66 in the market portfolio − $0.50 in small caps + $0.50 in large caps + $0.36 in value stocks − $0.36 in growth stocks− $0.04 in past winning stocks + $0.04 in past losing stocks.
Berkshire is adding 0.68% (alpha) relative to the above benchmark when adding the momentum factor.
Style analysis is a robust framework for handling time-varying benchmarks. William Sharpe (one of the inventors of the CAPM) introduced it in 1992. Style analysis is a factor benchmark with factor exposures evolving.
Consider the following funds:
Using the monthly data from January 2001 to December 2011, the following information is obtained by the extended Fama-French factor regressions using constant factor weights:
$$ \begin{align*} \begin{array}{l|c|c|c|c} {} & \textbf{LSVEX} & \textbf{FMAGX} & \textbf{GSCGX} & \textbf{BRK} \\ \hline \textbf{Alpha} & {0.00\%} & {-0.27\%} & {-0.14\%} & {0.22\%}\\ \hline \textbf{t-statistic} & {0.01} & {-2.23} & {-1.33} & {0.57}\\ \hline \text{MKT Loading} & {0.94} & {1.12} & {1.04} & {0.36}\\ \hline \textbf{t-statistic} & {36.90} & {38.60} & {42.20} & {3.77}\\ \hline \text{SMB Loading} & {0.01} & {-0.07} & {-0.12} & {-0.15}\\ \hline \textbf{t-statistic} & {0.21} & {-1.44} & {-3.05} & {-0.97}\\ \hline \text{HML Loading} & {0.51} & {-0.05} & {-0.17} & {0.34}\\ \hline \textbf{t-statistic} & {14.6} & {-1.36} & {-4.95} & {2.57}\\ \hline \text{WML Loading} & {0.20} & {0.02} & {0.00} & {-0.06} \\ \hline \textbf{t-statistic} & {1.07} & {1.00} & {-0.17} & {-0.77} \end{array} \end{align*} $$
Fidelity Magellan is the only alpha that is statistically significant at \(-0.27\%×12=-3.24\%\) per year. We can, therefore, conclude that Fidelity is not ‘adding alpha.’ Berkshire Hathaway’s alpha, on the other hand, is positive but insignificant. This is different from the alpha obtained earlier, from the data of the period starting from 1990. It is not easy to detect the statistical significance of outperformance.
LSV is a big value shop since it has a large HML beta of 0.51 with a massive t-statistic. Berkshire Hathaway is also a value shop with an HML beta of 0.34. None of these funds are momentum players since none of them has a large significant WML beta.
The following two potential shortcomings of our analysis can be rectified by style analysis:
The following are the issues that may arise when measuring the alpha for nonlinear strategies:
Empirical evidence has shown that a low-volatility stock earns higher risk-adjusted returns relative to the market portfolio, even after controlling for effects such as value and size. Using measures of market beta or volatility to sort stocks has provided proof of this anomaly. For instance, Friend and Blume (1970) used the stock portfolio returns in the period 1960 through 1968 with market beta and volatility risk measures. They showed an inverse relationship between returns and risk. Haugen and Heins (1975) used data from 1926 through 1971 to investigate the relation between market beta, volatility risk measures, and returns. They also came to a similar conclusion. In 2006, Andrew Ang et al. revived this study and found that the returns of high-volatility stocks had approximately zero average returns and that low-volatility stocks outperformed the high-volatility stocks.
$$ \text{Figure 1: Contemporaneous Volatility Portfolios} $$
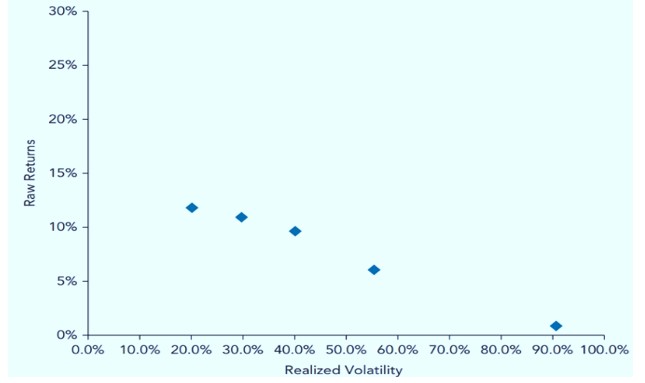
The beta anomaly occurs when stocks with high betas give lower risk-adjusted returns. The beta anomaly does not imply that stocks with high betas have low returns, but instead stocks with high betas tend to have high volatilities.
CAPM was first tested in the 1970s. These tests showed a positive relationship between beta and expected returns. It does not, however, imply that lagged betas lead to higher returns. The CAPM states that beta and expected returns have a contemporaneous relation. In particular, it predicts that stocks with higher betas will have higher average returns over the periods in which the betas and returns are measured.
Black, Jensen, and Scholes (1972), for example, found a positive relation between beta and returns, but they described it as being “too flat” relative to the CAPM predictions. Fama and French (1992), on the other hand, showed that beta and average returns had a statistically insignificant relationship. They showed that the point estimates indicated that the relation between beta and returns was negative.
Ang et al. (2006) showed that the average returns are approximately flat across the beta quintiles, around 15% for the first four quintiles, and 12.7% for the fifth quintile. Stocks with high betas tend to have high volatilities, causing the Sharpe ratios of high beta stocks to be lower than the Sharpe ratios of low-beta stocks.
The following are some of the possible explanations for the risk anomaly:
The low-risk effect has been witnessed in various contexts. As shown by Ang et al., the appearance of the effect is during recessions, expansions, periods of stability, and periods of volatility.
This happens also in international stock markets. As shown by Frazzini and Pedersen, high Sharpe ratios are witnessed in low-beta portfolios in U.S. stocks, international stocks, Treasury bonds, corporate bonds, Forex, and credit derivatives markets.
Since most investors wish to take on more risk but are unable to take on leverage, they become leverage constrained. They hold stocks that have built-in leverage since they cannot borrow. The bidding up of the high-beta stock’s price by investors goes on until the shares are overpriced and have low returns.
Unconstrained investors prefer buying low and selling high. For instance, they buy stocks with a positive alpha. Such stocks offer high returns. Likewise, they sell stocks with negative or low alpha, whose return is extremely low. In a perfect market, these investors would bid up the price of the first stock until it no longer has any excess returns. At the same time, they would sell the other stock until its returns reach a reasonable level. The risk anomaly automatically disappears. However, the market is not always perfect.
Asset owners may bid up certain stocks for which they have a preference due to their high volatility and high beta until their returns are lower. On the other hand, these investors may shun safe stocks due to their low volatility and low betas. This leads to lower prices and, hence, higher returns for these stocks.
Question 1
Barbara Flemings is a retail investor who expects her stock portfolio to return 11% in the following year. If the portfolio carries a standard deviation of 0.07, and the returns on risk-free Treasury notes are 3%, then which of the following is the closest to the Sharpe ratio of Flemings’ portfolio?
A. 1.14.
B. 0.08.
C. 0.0056.
D. 0.98.
The correct answer is A.
Remember that the Sharpe ratio is given as:
$$ \text{Sharpe Ratio=SR}=\frac { \overline { { r }_{ t }-{ r }_{ ft } } }{ \sigma } $$
Where:
\({ r }_{ t }=0.11\).
\({ r }_{ ft } =0.03\).
\(\sigma =0.07 \).
Therefore:
$$ \text{Sharpe Ratio}=\frac { 0.11-0.03 }{ 0.07 }=1.14 $$
This means that for every point of return, Flemings is shouldering 1.14 “units” of risk.
Question 2
A seasoned investment advisor at a leading asset management firm is discussing investment techniques during a seminar for recently recruited financial analysts. The topic shifts to the merits and drawbacks of low volatility investment tactics. The advisor showcases the historical track record of portfolios employing these strategies and underscores the significance of selecting appropriate benchmarks. Which of the following assertions regarding low volatility investment approaches would be accurate for the advisor to present during this seminar?
A. Employing these strategies often results in notable alpha when compared to standard market capitalization-oriented benchmarks.
B. These strategies typically produce negative alphas when pitted against dynamic elements like value or growth trajectories.
C. When contrasted with the risk-free rate, these strategies usually yield considerable alpha, but when compared to most benchmarks, the alpha tends to be insignificant.
D.The alphas generated by these strategies are usually lower when matched with risk-adjusted benchmarks but are considerably higher otherwise.
Solution
The correct answer is A.
Low volatility investment strategies, which inherently focus on assets with reduced price fluctuations, have consistently demonstrated a propensity to outperform traditional market capitalization-oriented benchmarks. At first glance, it might seem counterintuitive; after all, by prioritizing lower risk, one might anticipate a commensurate reduction in return. Yet, empirical data has often shown the opposite. These strategies, by effectively sidestepping more turbulent market swings and focusing on stable, consistent assets, have been able to achieve returns that are not just comparable but, in many cases, superior to their market-cap counterparts. This enhanced performance relative to the anticipated risk denotes a significant positive alpha, which is the excess return of an investment relative to the return of a benchmark index.
B is incorrect. While there might be instances where portfolios based on value or growth outdo low volatility portfolios, it doesn’t imply that the latter consistently yield negative alphas against these dynamic elements.
C is incorrect. While the alpha generated by low volatility strategies may vary depending on the benchmark used, to assert that it’s “insignificant” against most benchmarks is an overreach. In many instances, as demonstrated by historical data, low volatility strategies have indeed outperformed various benchmarks, not just the risk-free rate.
D is incorrect. Alpha is very much dependent on the benchmark used as well as whether or not that benchmark is adjusted for risk.
Things to Remember
- Low volatility investment strategies focus on assets with minimized price fluctuations.
- Alpha represents the excess return of an investment in relation to a benchmark index’s return.
- Choosing an appropriate benchmark is crucial in assessing the performance of any investment strategy, including low volatility ones.