High-level Summary of Basel III Reforms
After completing this reading, you should be able to: Explain the motivations for revising... Read More
After completing this reading, the candidate should be able to:
Operational risk is defined as the risk of loss resulting from inadequate or failed internal processes, people, and systems or from external events. It includes events such as fraud, employee errors, criminal activity, and security breaches. However, this definition excludes reputational risk as well as strategic risk.
Following the announcement of Basel III reforms, operational risk should be measured using the standardized approach in internationally active banks. It is, indeed, noteworthy that supervisors still have the discretion to apply the standardized approach among non-internationally active lenders.
The minimum operational risk capital (ORC) for a bank is given by:
$$ ORC = BIC × ILM $$
The Business Indicator Component (BIC) is a product of the Business Indicator (BI) and a set of regulatory marginal coefficients \( { a }_{ i } \).
$$ \left( BIC \right) =\sum { \left( { a }_{ i }\times { BI }_{ i } \right) } $$
The BI consists of select items from a bank’s financial statements that are representative of a bank’s operational risk exposure. In particular, the BI has 3 components:
Important: All the three components must be calculated as averages over 3 years.
The BIs of large international banks are typically large figures running into billions of Euros – the chosen denomination for operational risk capital calculations. A bank’s BI tells a lot about its operational risk exposure. For this reason, the standardized approach divides banks into 3 buckets according to the size of their BI. Each bucket is associated with a regulatory-determined coefficient \( { a }_{ i } \). As the BI increases, so do the coefficients. A summary is set out in the table below:
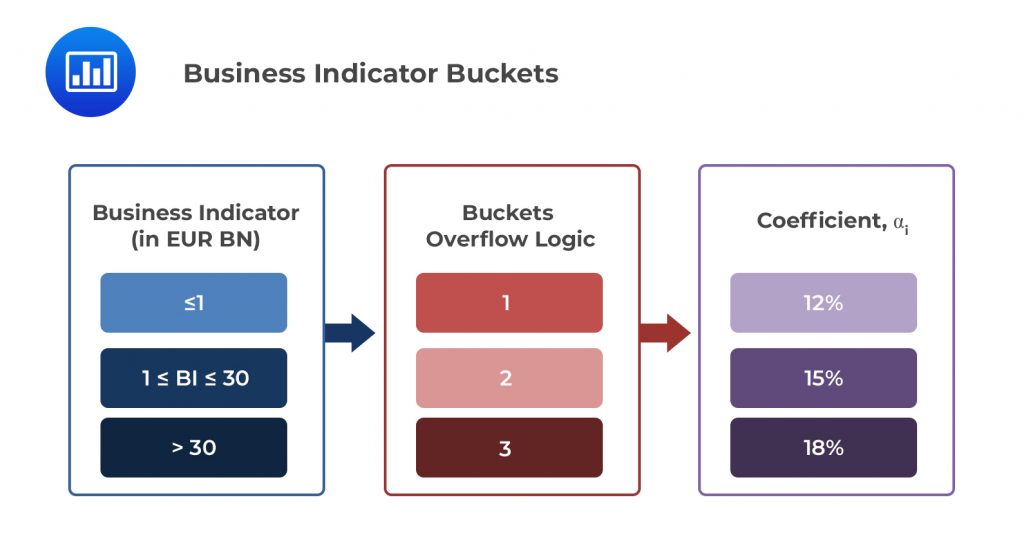 Example 1: Calculating the BIC of a Bank With a BI of €40bn.
Example 1: Calculating the BIC of a Bank With a BI of €40bn.$$
\small{\begin{array}{l|c|c|c}
\textbf{BI Bucket}& \textbf{1} & \textbf{2}& \textbf{3} \\ \hline
\textbf{BI Range} & ≤ €1 \text{ billion} & €1 \text{ billion} < BI ≤ €30 \text{ billion} & ≥€30 \text{ billion} \\ \hline
\textbf{Marginal BI Coefficient, } \bf{{ a }_{ i }} & 0.12 & 0.15 & 0.18 \\ \hline
\textbf{Calculation, } \bf{{ a }_{ i }} & €1bn × 12\%
= €0.12bn & €(30 – 1) × 15\%
= €4.35bn & €(40 – 30) × 18\%
= €1.8bn \\
\end{array}
}$$
By summing the 3 buckets, we arrive at a BIC of €6.27 billion.
$$
\small{\begin{array}{l|c|c|c}
\textbf{BI Bucket}& \textbf{1} & \textbf{2}& \textbf{3} \\ \hline
\textbf{BI Range} & ≤ €1 \text{ billion} & €1 \text{ billion} < BI ≤ €30 \text{ billion} & ≥€30 \text{ billion} \\ \hline
\textbf{Marginal BI Coefficient, } \bf{{ a }_{ i }} & 0.12 & 0.15 & 0.18 \\ \hline
\textbf{Calculation, } \bf{{ a }_{ i }} & €1bn × 12\%
= €0.12bn & €(25 – 1) × 15\% = €3.6bn & \\
\end{array}}
$$
By summing the 3 buckets, we arrive at a BIC of €3.72 billion.
The internal Loss Multiplier is defined as:
$$ ILM=\ln { \left[ exp\left( 1 \right) -1+{ \left( \frac { LC }{ BIC } \right) }^{ 0.8 } \right] } $$
As can be seen from the equation above, the ILM (the Internal Loss Multiplier) is a function of the BIC and the Loss Component (LC), where the latter is equal to 15 times a bank’s average historical losses over the preceding 10 years. Firms with less than 10 years of data must use a minimum of 5 years of data while computing the average historical loss.
Important:
The AMA, introduced in Basel II, allows for the estimation of regulatory capital to be based on a diverse range of internal modeling practices conditional on supervisory approval. The method has had a significant degree of flexibility, meaning that banks have been at liberty to use slightly different models while calculating the capital required. This flexibility has resulted in the AMA being replaced since it has resulted in widely incomparable internal modeling practices. This has exacerbated variability in risk-weighted asset calculations and eroded confidence in risk-weighted capital ratios. The SMA has limited flexibility and requires banks to follow precise guidelines in the entire capital calculation process.
To use the Loss Component (LC), banks have to observe certain guidelines:
Practice Question
Calculate the BIC of a bank with a BI of €20bn.
A. €3.6 billion.
B.€2.4 billion.
C. €3 billion.
D. €2.97 billion.
Solution
The correct answer is D.
$$
\small{\begin{array}{l|c|c|c}
\textbf{BI Bucket}& \textbf{1} & \textbf{2}& \textbf{3} \\ \hline
\textbf{BI Range} & ≤ €1 \text{ billion} & €1 \text{ billion} < BI ≤ €30 \text{ billion} & ≥€30 \text{ billion} \\ \hline
\textbf{Marginal BI Coefficient, } \bf{{ a }_{ i }} & 0.12 & 0.15 & 0.18 \\ \hline
\textbf{Calculation, } \bf{{ a }_{ i }} & €1bn × 12\%
= €0.12bn & €(20 – 1) × 15\% = €2.85bn & \\
\end{array}}
$$By summing the 2 buckets, we arrive at a BIC of €2.97 billion.