Option Sensitivity Measures: The “Greeks”

After completing this reading you should be able to:

• Describe and assess the risks associated with naked and covered option positions.
• Describe the use of a stop-loss hedging strategy, including its advantages and disadvantages, and explain how this strategy can generate naked and covered option positions.
• Compute the delta of an option.
• Explain delta hedging for an option position, including its dynamic aspects.
• Define and describe vega, gamma, theta, and rho for option positions and calculate the gamma and vega of an option.
• Explain how to implement and maintain a delta-neutral and gamma-neutral position.
• Describe the relationship between delta, theta, gamma, and vega.
• Calculate the delta, gamma, and vega of a portfolio.
• Describe how to implement portfolio insurance and how this strategy compares with delta hedging.

Risks Associated with Naked and Covered Option Positions

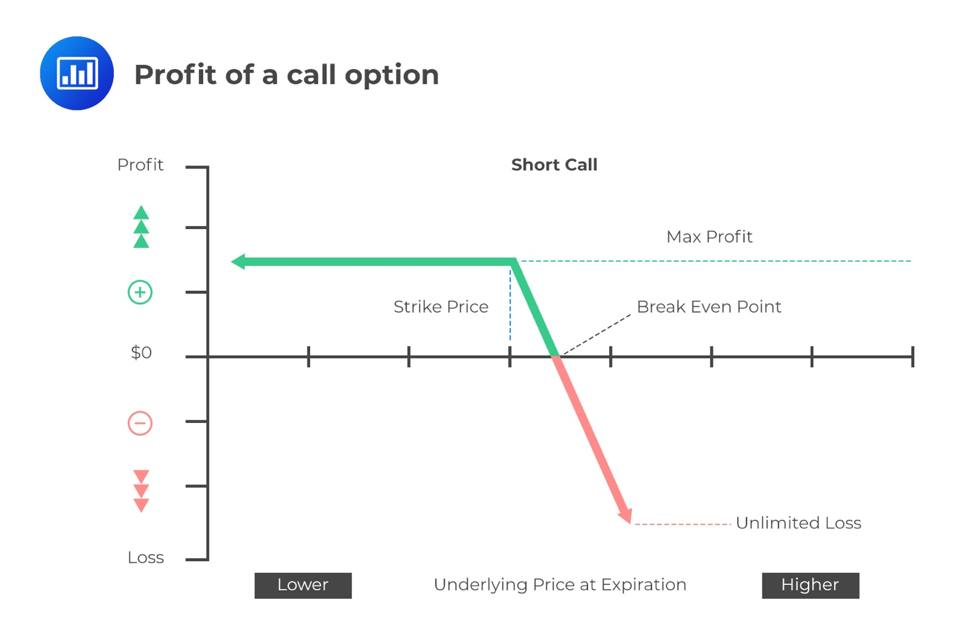
A naked option position occurs when a trader sells a call option without insurance in the form of a holding of the underlying shares. If the option position is backed by ownership of the underlying shares, the position is said to be covered (clothed).

Selling naked call options is laden with risks on the part of the trader. If the market price is below the pre-agreed strike price on the expiration date, the seller makes a gain equal to the premium received. However, if the market price soars above the strike price as at expiration, the buyer exercises the option. When that happens, the seller has to deliver the agreed number of shares to the buyer, even if it means buying from the market. Depending on the extent of the price increase, the entire loss arising from a naked option can be absorbed by the premium received. In other cases, the price increase may be so high that the seller is left with a net loss.

On the contrary, the trader may insure themselves by selling covered options. This may be a safer strategy but one that’s also laden with downside risk. If the stock falls, the seller will get to keep the entire premium, but the shares under their ownership will now be worthless. Sometimes the price fall may be too high such that the total value lost in the long position exceeds the premium received.

Example:

Suppose a firm sells 10,000 naked call options on a stock on a stock currently going for $30 a share. The strike price is $33 and the option premium is $4

Scenario 1: Price at expiry = $29

The buyer will not exercise the premium. Total income generated \(=10,000 \times $4=$40,000\)

Scenario 2: Price at expiry = $37

The buyer will exercise the options, and the seller is obliged to honor the contract. As such, the seller buys 10,000 shares from the market at a cost of $37 per share and hands them to the buyer.

$$\begin{align*} \text{Net loss}&=\text{premium received}+\text{contract proceeds}-\text{cost of shares delivered}\\ &=$4\times 10,000+$33\times 10,000-$37\times 10,000=$0 \end{align*}$$

In this scenario, the loss is absorbed by the premium, resulting in a net loss of $0

Scenario 3: Price at expiry = $38

Again, the buyer exercises the options.

$$\begin{align*} \text{Net loss}&=\text{premium received}+\text{contract proceeds}-\text{cost of shares delivered}\\ &=$4\times 10,000+$33\times 10,000-$38\times 10,000=$10,000 \end{align*} $$

How Naked and Covered Option Positions Generate a Stop Loss Trading Strategy

A stop-loss trading strategy is a strategy where the trader initially gets into a naked option position but later on seeks cover when the option moves in-the-money. In other words, protection is sought only when market conditions are such that the call writer stands to lose.

With a naked call position, this strategy requires the purchase of the underlying asset immediately the market price rises above the option’s strike price. But as soon as the market price returns to a position that’s below the strike price, the trader sells the underlying asset.

Although this sounds like a simple, executable plan on paper, it’s a lot more complicated in practice thanks to transaction costs and price uncertainty. In practice, buy/sell costs increase as fluctuations in the strike price increase. It also becomes even more difficult to predict whether the option will be in-the-money or out-of-the-money at expiration.

Delta of an Option

Delta is a measure of the degree to which an option is exposed to changes in the price of the underlying asset. It’s the ratio of the change in the price of the call option to the change in the price of the underlying.

$$ \text{Delta}=\Delta =\frac { \text{change in the call option price} }{ \text{change in the price of the underlying}} $$

For example, if we have a delta value of 0.5, it means that when the price of the underlying moves by a point, the price of the corresponding call option will change by half a point. If delta = 0.5, a $1 increase in the underlying’s price triggers a $0.5 increase in the price of the call option.

How to Compute Delta of an Option

Call Option

Delta of a Call option is closely related to \( N\left( { d }_{ 1 } \right) \) in the Black-Scholes Pricing model. Precisely,

$$ { \Delta }_{ c }={ e }^{ -qT }N\left( { d }_{ 1 } \right) $$

Where

\( { d }_{ 1 }=\frac { ln\frac { S }{ K } +\left( r+\frac { { \sigma }^{ 2 } }{ 2 } \right) T }{ \sigma \sqrt { T } } \)

\(q\) is the dividend yield(%)

\(S\)=price of the underlying

\(K\)=strike price of the option

\(r\)=risk-free interest rate

\(\sigma\)=volatility of the underlying

\(T\)=time to option’s expiry

Exam tips:

1. Delta of a call option is always positive (between 0 and 1). The delta of an at-the-money call option is close to 0.5. Delta moves to 1 as the call goes deep in-the-money (ITM). It moves to zero as the call goes deep out-of-the-money (OTM).
2. If the underlying does not pay dividends the delta of a call option simplifies to:$$ { \Delta }_{ c }={ e }^{ -qT }N\left( { d }_{ 1 } \right) ={ e }^{ 0 }N\left( { d }_{ 1 } \right) =N\left( { d }_{ 1 } \right) $$(\(q\) is zero in this case, and any number raised to power zero is equal to 1)

Put option

The delta of a put option is

$$ { \Delta }_{ p }={ e }^{ -qT }\left[ N\left( { d }_{ 1 } \right) -1 \right] $$

It behaves similar to the call delta, except for the sign (between 0 and -1). As with the call delta, if there are no dividends,

$$ { \Delta }_{ p }={ e }^{ 0 }\left[ N\left( { d }_{ 1 } \right) -1 \right] =\left[ N\left( { d }_{ 1 } \right) -1 \right] $$

Exam tip: The delta of an at-the-money put option is close to -0.5. Delta moves to -1 as the put goes deep in-the-money. It moves to zero as the put goes deep out-of-the-money.

Dynamic Aspects of Delta Hedging for an Option Position

Delta hedging is an attempt to reduce (hedge) the risk associated with price movements in the underlying, by offsetting long and short positions. For instance, a long call position could be offset by shorting the underlying stock. Since delta is actually a function of the price of the underlying asset, it continually changes as the underlying’s price changes.

When delta changes, the initially option-hedged position is, again, thrust into a state of imbalance. In other words, the number of stocks is no longer matched with the right number of options, exposing the trader to possible loss.

The overall goal of delta-hedging (a delta-neutral position) is to combine a position in the underlying with another position in an option such that the value of the portfolio remains fixed even in the face of constant changes in the value of the underlying asset.

Delta Hedging with Options

Sometimes an options position can be delta hedged using another options position that has a delta that’s opposite to that of the current position. This effectively results in a delta-neutral position. For instance, suppose an investor holds a one call option position with a delta of 0.5. A call with a delta of 0.5 means it is at-the-money. To maintain a delta neutral position, the trader can purchase an at-the-money put option with a delta of -0.5, so that the two cancel out.

Theta, Gamma, Vega, and Rho for Option Positions

Theta

Theta, \(\theta \), tells us how sensitive an option is to a decrease in time to expiration. It gives us the change in the price of an option for a one-day decrease in its time to expiration.

Options lose value as expiration approaches. Theta estimates the value lost per day if all other factors are held constant. Time value erosion is nonlinear, and this has implications on theta. As a matter of fact, the theta of at-the-money options generally increases as expiration nears. On the other hand, the theta of out-of-the-money or in-the-money options generally decreases as expiration nears.

For a call option,

$$ \theta =\frac { \partial c }{ \partial t } $$

Where:

\( { \partial c }\)=change in call price

\({ \partial t }\)=change in time

For European call options that have zero dividends, the Black-Scholes Merton model can be used to calculate theta. Precisely,

$$\begin{align*} { \theta }_{ \text{call} }&=-\frac { { S }_{ 0 }{ N }^{ \prime }\left( { d }_{ 1 } \right) \sigma }{ 2\sqrt { T } } -rX{ e }^{ -rT }N\left( { d }_{ 2 } \right) \\ { \theta }_{ \text{put} }&=-\frac { { S }_{ 0 }{ N }^{ \prime }\left( { d }_{ 1 } \right) \sigma }{ 2\sqrt { T } } +rX{ e }^{ -rT }N\left( -{ d }_{ 2 } \right) \end{align*} $$

Where:

$$ { N }^{ \prime }\left( y \right) =\frac { 1 }{ \sqrt { 2\pi } } { e }^{ -\left( \frac { { y }^{ 2 } }{ 2 } \right) },y={ d }_{ 1 },{ d }_{ 2 } $$

In the above equations, the resulting value for theta is measured in years because \(T\) is also measured in years. To convert theta into a daily value, divide by 252, assuming 252 trading days in a year.

Gamma

Gamma, \(\Gamma \), measures the rate of change in an option’s Delta per $1 change in the price of the underlying stock. It tells us how much the option’s delta should change as the price of the underlying stock or index increases or decreases. Options with the highest gamma are the most responsive to changes in the price of the underlying stock.

Mathematically,

$$ \Gamma =\frac { { \partial }^{ 2 }c }{ { \partial }S^{ 2 } } $$

Where the numerator and denominator are the partial derivatives of the call and stock prices, respectively.

For European calls and puts on stocks with zero dividends,

$$ \Gamma =\frac { { N }^{ \prime }\left( { d }_{ 1 } \right) }{ { S }_{ 0 }\sigma \sqrt { T } } $$

Implementing and Maintaining Delta-neutral and Gamma-neutral Positions

While delta-neutral positions hedge against small changes in stock price, gamma-neutral positions guard against relatively large stock price moves. As such, a delta-neutral position is important, but even more important is one that’s also gamma-neutral, because it will be insulated from both small and large price moves.

The number of options that must be added to an existing portfolio to generate a gamma-neutral position is given by:

$$ -\left( \frac { { \Gamma }_{ p } }{ { \Gamma }_{ T } } \right) $$

Where:

\({ \Gamma }_{ p } \)=gamma of the existing portfolio position

\({ \Gamma }_{ T }\)=gamma of a traded option that can be added

Example on Delta-Gamma Hedging

A trader has a short option position that’s delta-neutral but has a gamma of -800. In the market, there’s a tradable option with a delta of 0.8 and a gamma of 2. To maintain the position gamma-neutral and delta-neutral, what would be the trader’s strategy?

The number of options that must be added to an existing portfolio to generate a gamma-neutral position is given by:

$$ −\frac { { \Gamma }_{ p } }{ { \Gamma }_{ T } }=-\frac {−800}{2}=400 $$

Buying 400 calls, however, increases delta from zero to 320 (=400×0.8). Therefore, the trader has to sell 320 shares to restore the delta to zero. Positions in shares always have zero gamma.

Relationship among Delta, Theta, and Gamma

The relationship between the three Greeks can best be expressed in the following equation:

$$ rP=\theta +rS\Delta +0.5{ \sigma }^{ 2 }{ S }^{ 2 }\Gamma $$

Where:

\(r\)=risk neutral risk-free rate

\(P\)=price of the option

\(\theta\)=option theta

\(S\)=price of the underlying stock

\(\Delta\)=option delta

\({ \sigma }^{ 2 }\)=variance of the underlying stock

\(\Gamma\)=option Gamma

If a position is delta-neutral, then \(\Delta=0\), and the above equation narrows down to:

$$ rP=\theta +0.5{ \sigma }^{ 2 }{ S }^{ 2 }\Gamma $$

Vega

Vega measures the rate of change in an option’s price per 1% change in the implied volatility of the underlying stock. And while Vega is not a real Greek letter, it tells us how much an option’s price moves in response to a change in volatility of the underlying.

As an example, a Vega of 6 indicates that for a 1% increase in volatility, the option’s price will increase by 0.06. For a given exercise price, risk-free rate, and maturity, the Vega of a call equals the Vega of a put.

Mathematically,

$$ Vega=\frac { \partial c }{ \partial \sigma } $$

Where:

\({ \partial c }\)=change in call price

\({ \partial \sigma }\)=change in volatility

For European calls and puts on stocks with zero dividends,

$$ Vega=S_{ 0 }{ N }^{ \prime }\left( { d }_{ 1 } \right) \sqrt { T } $$

A drop in Vega will typically cause both calls and puts to lose value. An increase in Vega will typically cause both calls and puts to gain value.

Vega decreases with maturity, unlike gamma which increases with maturity. Vega is highest for at-the-money options.

Rho

Rho measures the expected change in an option’s price per 1% change in interest rates. It tells us how much the price of an option should fall or rise in response to an increase or decrease in the risk-free rate of interest.

As interest rates increase, the value of call options will generally increase. On the other hand, as interest rates increase, the value of put options will usually decrease. Although rho is not a dominant factor in the price of an option, it takes center stage when interest rates are expected to change significantly.

Long-term options are far more sensitive to changes in interest rates than are short-term options. Furthermore, in-the-money calls and puts are more sensitive to interest rate changes compared to out-of-the-money calls and puts.

Mathematically,

$$ rho=\frac { \partial c }{ \partial r } $$

Where:

\({ \partial c }\)=change in call price

\({ \partial r }\)=change in interest rate

For European calls and puts on stocks that do not pay dividends,

$$ \begin{align*} { rho }_{ call }&=XT{ e }^{ -rT }N\left( { d }_{ 2 } \right)\\ { rho }_{ put }&=-XT{ e }^{ -rT }N\left( -{ d }_{ 2 } \right) \end{align*} $$

Calculating Delta, Gamma, and Vega of a Portfolio

Delta of a Portfolio

Suppose we want to determine the delta of a portfolio of options, all on a single underlying. The portfolio delta is equivalent to the weighted average of the deltas of individual options.

$$ \text{portfolio delta}={ \Delta }_{ \text{portfolio} }=\sum _{ i=1 }^{ n }{ { w }_{ i }{ \Delta }_{ i } } $$

\({ w }_{ i }\) represents the weight of each option position while \({ \Delta }_{ i } \) represents the delta of each option position.

For example, if a portfolio includes a long position of 50,000 call options with a delta per option of 0.46, a short position of 20,000 call options with a delta of 0.33, and a short position in 30,000 put options with a delta of -0.54, the portfolio’s delta is calculated as follows:

\[ \text{Portfolio Delta} = 50,000 \times 0.46 – 20,000 \times 0.33 – 30,000 \times (-0.54) = 32,600 \]

Gamma for a Portfolio

Gamma quantifies the rate of change of delta as the stock price changes. Calculating the gamma of a portfolio involves the sum of products of the number of options and their gammas. Referring to the same example portfolio:

\[ \text{Portfolio Gamma} = 50,000 \times 0.13 – 20,000 \times 0.15 – 30,000 \times 0.08 = 1,100 \]

Vega for a Portfolio

Vega measures the portfolio’s sensitivity to a 1% change in the implied volatility of the underlying stock. Vega for the portfolio is found by adding the products of the number of options and their vegas:

\[ \text{Portfolio Vega} = 50,000 \times 3.3 – 20,000 \times 4.2 – 30,000 \times 3.0 = -9,000 \]

Creating Portfolio Insurance through Option Instruments and Stock Index Futures

Portfolio insurance is the combination of (1) an underlying instrument and (2) either cash or a derivative that generates a minimum value for the portfolio in the event that markets crash and values decline, while still allowing the trader to make a gain in the event that market values rise. The degradation of portfolio value is protected.

The most common insurance strategy involves using put options to lock in the value of an asset. This way, the trader is able to maintain a limit on the portfolio value – even if the underlying’s price tumbles, the trader is insulated from prices below the put’s strike.

To hedge a portfolio with index options, the trader selects an index with a high correlation to their portfolio. For instance, if the portfolio consists of mainly technology stocks, the Nasdaq Composite Index might be a good fit. If the portfolio is made up of mainly blue-chip companies, then the Dow Jones Industrial Index could be used.

Alternatively, a trader can use stock index futures with a similar end goal. Traders who want to hedge their portfolios need to calculate the amount of capital they want to hedge and find a representative index. Assuming an investor wants to hedge a $500,000 stock portfolio, she would sell $500,000 worth of a specific futures index, such as the S&P 500.

Practice Questions

Question 1

The current stock price of a company is USD 100. A risk manager is monitoring call and put options on the stock with exercise prices of USD 70 and 6 days to maturity. Which of these scenarios is most likely to occur if the stock price falls by USD 1?

$$
\begin{array}{c|l|l}
\textbf{Scenario} & \textbf{Call Value} & \textbf{Put Value} \\ \hline
A & \text{Decrease by } $0.9 & \text{Increase by } $0.05 \\ \hline
B & \text{Decrease by } $1 & \text{Increase by } $1 \\ \hline
C & \text{Decrease by } $0 & \text{Increase by } $1 \\ \hline
D & \text{Decrease by } $0 & \text{Increase by } $0 \\
\end{array}
$$

The correct answer is A.

The call option is deep-in-the-money and therefore must have a delta close to one. The put option is deep out-of-the-money and will, therefore, have a delta close to zero. Therefore, the value of the in-the-money call will decrease by close to USD 1, and the value of the out-of-the-money put will increase by a much smaller amount close to 0. Among the four choices, it’s A that is closest to satisfying both conditions.

Question 2

\(XYZ\) Inc., a non-dividend-paying stock, has a current price of $200 per share. Eric Rich, FRM, has just sold a six-month European call option contract on 200 shares of this stock at a strike price of $202 per share. He wants to implement a dynamic delta hedging scheme to hedge the risk of having sold the option. The option has a delta of 0.50. He believes that the delta would fall to 0.40 if the stock price falls to $195 per share.

Identify what action he should take NOW (i.e., when he has just written the option contract) to make his position delta-neutral

After the option is written, if the stock price falls to $195 per share, identify the action Mr. Rich should take at that time, i.e. LATER, to rebalance his delta-hedged position

1. NOW: buy 200 shares of stock, LATER: buy 100 shares of stock
2. NOW: buy 100 shares of stock, LATER: sell 20 shares of stock
3. NOW: sell 100 shares of stock, LATER: buy 100 shares of stock
4. NOW: sell 100 shares of stock, LATER: buy 20 shares of stock

The correct answer is B.

NOW: Eric sold a call on 200 shares, that means he’s short delta of \(0.50\times 200\), which is delta = -100. To be delta neutral, he must long (i.e. buy) 100 shares of stock.

LATER: As price falls to $195, the delta moves to \(-80=-0.40\times 200\). To be delta neutral, Eric’s portfolio needs to have 80 shares of stock. He purchased 100 shares at time 0. To rebalance, he must sell 20 shares.