GARP Code of Conduct
After completing this reading, you should be able to: Describe the responsibility of... Read More
p>
After completing this reading, you should be able to:
This chapter discusses one-factor risk metrics, which include DV01, duration, and convexity, as used in the analysis of fixed-income portfolios. We consider these measures to quantify the consequence of a parallel shift in the interest rate term structure: DV01 and duration consider a small parallel shift in the term structure while convexity extends the duration to accommodate larger parallel shifts. Hedging can, in accordance with these risk metrics, be efficient for a parallel shift of term structure as compared to non-parallel shifts.
The one-factor assumption states that when the rates are driven by one factor, the change of one interest rate can be used to determine the change in all other interest rates over a short period of time. For instance, a one-factor model assumes that all interest rates changes by the same amount. As such, the shape of the term structure never changes. That is, if a one-year spot rate increases by two basis points, all other spot rates increase by two basis points. DV01, duration, and convexity are examples of such models.
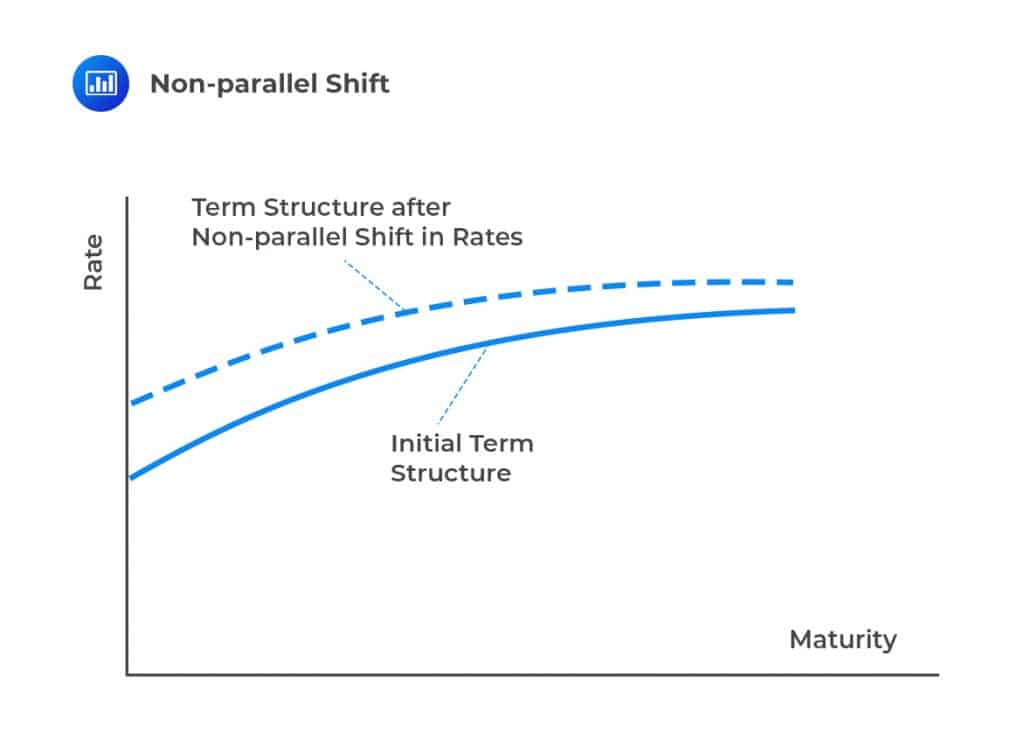
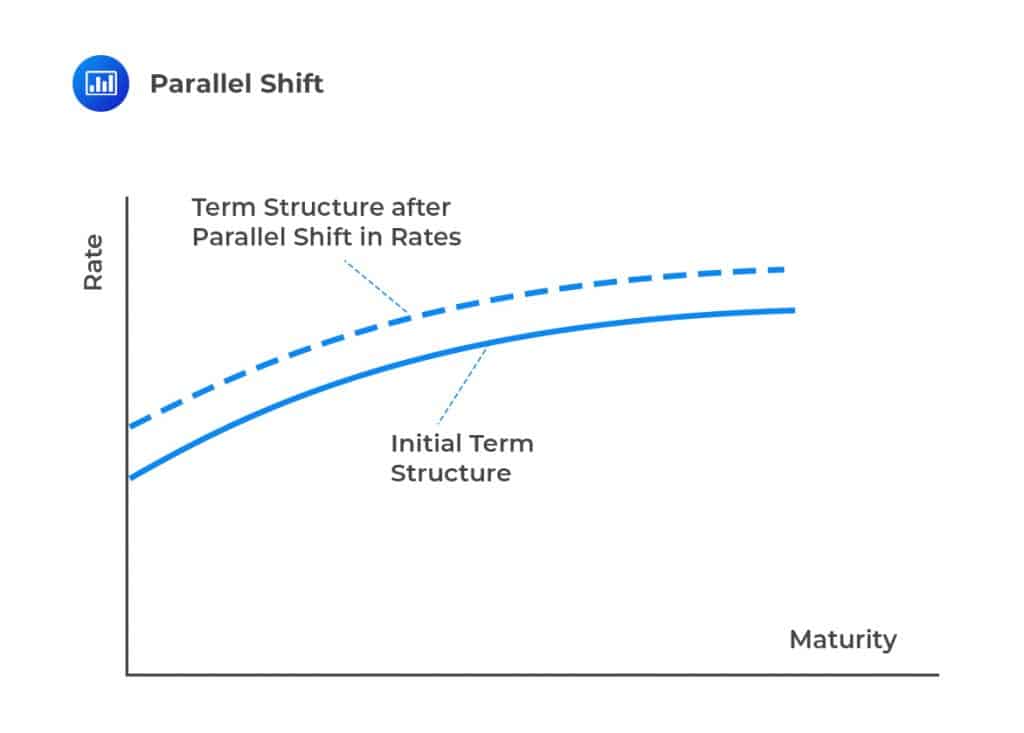 It is worth noting that shifts in the term structure are not always parallel. For instance, a one-factor model might predict that if the one-year spot rate increases by five basis points over a short period, then the two-year increases by three basis points, and the ten-year rate increases by one basis point.
It is worth noting that shifts in the term structure are not always parallel. For instance, a one-factor model might predict that if the one-year spot rate increases by five basis points over a short period, then the two-year increases by three basis points, and the ten-year rate increases by one basis point.
 DV01 of a Fixed-income Security
DV01 of a Fixed-income SecurityDV01 reflects the effect of a one-basis movement in interest rates on the value of a portfolio. DV01 is defined as:
$$ \text{DV01}=-\cfrac { \Delta \text{P} }{ \Delta \text{r} } $$
Where
\({ \Delta \text{r} } \) = the size of a parallel shift in the interest rate term structure measured in basis points
\({ \Delta \text{P} } \) = resultant change in the value of the position being considered
Note that for a long position in bonds, the DV01 is positive due to a negative correlation between the bond’s price and interest rate changes.
DV01 is defined in three different ways:
A two-year treasury bond has a face value of USD 100,000, with an annual coupon rate of 8% paid semiannually. The spot rates, as shown in the table below:
$$ \begin{array}{c|c} \textbf{Maturity Period (Years)} & \textbf{Spot Rate (%)} \\ \hline {0.5} & {6.0} \\ \hline {1.0} & {6.5} \\ \hline {1.5} & {7.0} \\ \hline {2.0} & {7.5} \\ \end{array} $$
What is the value of the DV01 if:
i. The price of a bond with no spread is USD 101,003.01 calculated using the formula:
$$ \text{P}=\cfrac { \text{C} }{ 2 } \sum _{ \text{i}=1 }^{ 2\text{T} }{ { \left( \cfrac { 1 }{ 1+\cfrac { \text{y} }{ 2 } } \right) }^{ i } } +\cfrac { 100,000 }{ { \left( 1+\cfrac { \text{y} }{ 2 } \right) }^{ 2\text{T} } } $$
In this case,
$$ \text{c}=100,000\times0.08=8,000, \text{T}=2 $$
$$ \begin{align*} \Rightarrow \text{p} & =\cfrac { 8000 }{ 2 } \left( \cfrac { 1 }{ 1+\cfrac { 0.06 }{ 2 } } +\cfrac { 1 }{ { \left( 1+\cfrac { 0.065 }{ 2 } \right) }^{ 2 } } +\cfrac { 1 }{ { \left( 1+\cfrac { 0.07 }{ 2 } \right) }^{ 3 } } +\cfrac { 1 }{ { \left( 1+\cfrac { 0.075 }{ 2 } \right) }^{ 4 } } \right) +\cfrac { 100,000 }{ { \left( 1+\cfrac { 0.075 }{ 2 } \right) }^{ 4 } } \\ & =4000\left( \cfrac { 1 }{ 1.03 } +\cfrac { 1 }{ { \left( 1.0325 \right) }^{ 2 } } +\cfrac { 1 }{ { \left( 1.035 \right) }^{ 3 } } +\cfrac { 1 }{ { \left( 1.0375 \right) }^{ 4 } } \right) +\cfrac { 100,000 }{ { \left( 1.0375 \right) }^{ 4 } } \\ & =101,003.01 \end{align*} $$
If the spot rates are each increased by 5 basis points (0.05%) so that the six-month spot rate is 6.05%, the one-year spot rate is 6.55%, and so on, the price of the bond is USD 100,911.18, calculated as:
$$ \begin{align*}&=\cfrac { 8000 }{ 2 } \left( \cfrac { 1 }{ 1.03025 } +\cfrac { 1 }{ { \left( 1.03275 \right) }^{ 2 } } +\cfrac { 1 }{ { \left( 1.03525 \right) }^{ 3 } } +\cfrac { 1 }{ { \left( 1.03775 \right) }^{ 4 } } \right) +\cfrac { 100,000 }{ { \left( 1.03775 \right) }^{ 4 } } \\ &=100,911.18 \end{align*}$$
We know that:
$$ \begin{align*} \text{DV01} & =-\cfrac { \Delta \text{P} }{ \Delta \text{r} } = -\cfrac {100,911.18-101,003.01}{5} \\ & =\cfrac {91.83}{5}=18.366 \end{align*} $$
Note that the rise of the spot rates by 5 basis points decreases the bond price by 91.83 (=100,911.18 − 101,003.01), and the DV01, in this case, measures the decline of a bond price for each one-basis point increase in spot rates.
ii. Assume now that the spot rates decrease by 5 basis points so that the six-month spot rate is 5.95% (=6 − 0.05), the one-year spot rate is 6.45% (=6.5 − 0.05) and so on. Under decreased spot rates, the price of the bond is USD 101,094.96 calculated as
$$ =4,000\left( \cfrac { 1 }{ 1.02975 } +\cfrac { 1 }{ { \left( 1.03225 \right) }^{ 2 } } +\cfrac { 1 }{ { \left( 1.03475 \right) }^{ 3 } } +\cfrac { 1 }{ { \left( 1.03725 \right) }^{ 4 } } \right) +\cfrac { 100,000 }{ { \left( 1.03725 \right) }^{ 4 } } =101,094.96\\ \\ \\ $$
And thus,
$$ \begin{align*} \text{DV01} & =-\cfrac { \Delta \text{P} }{ \Delta \text{r} } = -\cfrac {101,094.96-101,003.01}{-5} \\ & =\cfrac {91.95}{-5}=18.39 \end{align*} $$
As such, an increase of spot rates by five basis points causes the price of the bond to increases by 91.95 (=101,094.96 − 101,003.01), and thus DV01, in this case, measures the increase of bond price for each one-basis point decrease in spot rates.
It is worth noting that the DV01 for the decrease and increases of the basis points are slightly different because the bond price is not a linear function of interest rates. We estimate the DV01 by averaging the estimates above:
$$ \text{DV01}=\cfrac {18.366+18.39}{2}=18.38 $$
Assume that now bond yield increases by one basis point. Consider the spot rates, as in the example above.
$$ \begin{array}{c|c} \textbf{Maturity Period (Years)} & \textbf{Spot Rate (%)} \\ \hline {0.5} & {6.0} \\ \hline {1.0} & {6.5} \\ \hline {1.5} & {7.0} \\ \hline {2.0} & {7.5} \\ \end{array} $$
A two-year treasury bond has a face value of USD 100,000, with an annual coupon rate of 8% paid semiannually. The spot rates, as shown in the table above.
What is the value of DV01 if the bond yield
Recall that, using the spot rates, we calculated the bond price to be 101,003.01. To find the yield to maturity of the bond (bond yield), we solve the equation:
$$ \cfrac { 4,000 }{ 1+\cfrac { \text{y} }{ 2 } } +\cfrac { 4,000 }{ { \left( 1+\cfrac { \text{y} }{ 2 } \right) }^{ 2 } } +\cfrac { 4,000 }{ { \left( 1+\cfrac { \text{y} }{ 2 } \right) }^{ 3 } } +\cfrac { 104,000 }{ { \left( 1+\cfrac { \text{y} }{ 2 } \right) }^{ 4 } } =101,003.01 $$
Using a financial calculator with the variables N=4, PMT=4000, PV=−101,003.01, we get:
$$ \cfrac {\text{y}}{2}=3.7255\% \Rightarrow {\text{y}}=7.45\% $$
i. Now, if the bond yield increases by 5 basis point to 7.50% (=7.45 + 0.05), the price of the bond is 100,912.846 (using the financial calculator) and thus for an increase of 5 basis points in bond yield, the bond price decreases by 90.160 (=100,912.85 − 101,003.01). We can, therefore, calculate the DV01:
$$ \begin{align*} \text{DV01} & =-\cfrac { \Delta \text{P} }{ \Delta \text{r} } = -\cfrac {100,912.85-101,003.01}{5} \\ & =\cfrac {-90.16}{5}=18.032 \end{align*} $$
ii. Similarly, if the bond yield decreases by 5 basis points to 7.40% (=7.45 − 0.05), the bond price is 101,096.71. A decrease of bond yield by 5 basis points increases the bond price by 93.70 (=101,096.71 − 101,003.01). Thus,
Similarly, if the bond yield decreases by 5 basis points to 7.40% (=7.45 − 0.05), the bond price is 101,096.71. A decrease of bond yield by 5 basis points increases the bond price by 93.7(=101,096.71 − 101,003.01). Thus,
$$ \begin{align*} \text{DV01} & =-\cfrac { \Delta \text{P} }{ \Delta \text{r} } = -\cfrac {101,096.71-101,003.01}{-5} \\ & =\cfrac {-93.7}{5}=18.74 \end{align*} $$
The average of the estimates is 18.386 given as:
$$ \cfrac {18.032+18.74}{2}\approx 18.386$$
In the cases of the forward rates, the analogy is similar to that of the spot rates. However, this chapter will primarily emphasize on DV01 computed from a one-basis-point parallel shift in the term structure of spot rates.
Recall that DV01 is a measure that indicates the price change in a bond for a 1-basis-point move in interest rates. When employing DV01 for hedging, one matches the DV01 of the position to be hedged with the DV01 of the bonds used as a hedge. The objective is to create a position where the net DV01 is zero, effectively neutralizing interest rate risk.
For example, assume that a bank has a position whose DV01 is −40. By the definition of DV01, the banks will gain from their position if interest rates increases and will undoubtedly lose value if interest rates decrease. More specifically, if all the interest increases by the one-basis point, the value of the bank’s position increases by USD 40. On the contrary, if all interest rates decrease by one basis point, the value of the bank’s position decreases by USD 40.
Now assume that this bank wants to hedge its position with a coupon bond that pays an annual coupon rate of 8% payable semiannually, has a face value of USD 100,000, and a bond yield of 7.50%. If we can determine a position in the coupon bond that is exactly 40, the bank’s position would have been hedged.
A hedge ratio determines the amount of par of the hedge position that needs to be bought or sold for every $1 par value of the original position. The goal of hedging is to lock in the value of a position even in the face of small changes in yield. The hedge ratio is given by:
$$ \text{HR}=\cfrac { { \text{DV01} }_{ \text{Initial Position} } }{ { \text{DV01} }_{ \text{Hedge Position} } } $$
Assume that DV01 of the coupon bond is 18.33. We use the hedge ratio and the bond’s face value to increase the DV01 of the bond to 40. In this case, we need to increase the value of the position by:
$$ 100,000\times\cfrac {40}{18.33}=$218,221.50 $$
Thus, adding the USD 218,221.50 of coupon bond’s position to the bank’s portfolio protects against small changes in the term structure. In other words, a downward (upward) movement of the term structure will result in a gain (loss) on the existing position, which will be offset by a loss (gain) on the position in the 8% coupon bond.
Effective duration measures the percentage change in the price of a bond (or other instruments) caused by small changes in all rates. Note that effective duration is different from DV01 because DV01 measures actual price changes against small changes in all rates.
Effective duration is defined as:
$$ \text{D}=-\cfrac { \cfrac {\Delta \text{P}}{P} }{ \Delta \text{r} } = -\cfrac { \Delta \text{P} }{\text{P} \times \Delta \text{r} } $$
The effective duration can also be rewritten as:
$$ { \Delta \text{P} }=-{\text{D}}\times{\text{P}}\times{\Delta \text{r} } $$
When the change in all rates is measured basis points, the effective duration is equivalent to DV01 divided by the bond price.
Consider the DV01 example on the spot rates where we had calculated the price of the bond USD 101,003.01 and the DV01 of 18.38 so that the duration is:
$$ \cfrac {18.33}{101003.01}=0.000182=0.0182\% $$
Effective duration gives the proportional change in the price of an instrument corresponding to a one-basis point change in all interest rates.
Typically, the effective duration is stated as a percentage change in the price of an instrument for a 100-basis-change in all rates by multiplying the effect of one-basis-point change by 100. Therefore, our example above would be stated as 1.82% per 100 basis points.
However, for the sake of clarity, the duration in this chapter will be reported as a decimal. In the decimal reporting system, one basis point is equivalent to 0.0001, and thus, we measure duration per 10,000 basis points. Therefore, the duration calculated above will be:
$$ 0.000182\times10,000=1.82 $$
Convexity measures the sensitivity of duration measure to movement in the interest rates. Denote convexity by C and value of a position by P, convexity is defined as:
$$ \text{C}=\cfrac { 1 }{ \text{P} } \left[ \cfrac { { \text{P} }^{ + }+{ \text{P} }^{ – }-2\text{P} }{ { \left( \Delta \text{r} \right) }^{ 2 } } \right] $$
Where:
\({ { \text{P} }^{ + }}\) = the value of the position when all rates increase by \(\Delta \text{r}\)
\({ { \text{P} }^{ – }}\) = the value of the position corresponding to the decrease of all rates by \(\Delta \text{r}\)
Note that \(\Delta \text{r}\) is given in decimal.
A two-year treasury bond has a face value of USD 100,000, with an annual coupon rate of 8% paid semiannually. The spot rates, as shown in the table below:
$$ \begin{array}{c|c} \textbf{Maturity Period (Years)} & \textbf{Spot Rate (%)} \\ \hline {0.5} & {6.0} \\ \hline {1.0} & {6.5} \\ \hline {1.5} & {7.0} \\ \hline {2.0} & {7.5} \\ \end{array} $$
What is the value of the convexity if all spot rates change by 5 basis points?
As computed earlier, the price of a bond with no interest spread is USD 101,003.01 calculated as:
$$ \begin{align*} {\text{p}} & =\cfrac { 8000 }{ 2 } \left( \cfrac { 1 }{ 1+\cfrac { 0.06 }{ 2 } } +\cfrac { 1 }{ { \left( 1+\cfrac { 0.065 }{ 2 } \right) }^{ 2 } } +\cfrac { 1 }{ { \left( 1+\cfrac { 0.07 }{ 2 } \right) }^{ 3 } } +\cfrac { 1 }{ { \left( 1+\cfrac { 0.075 }{ 2 } \right) }^{ 4 } } \right) +\cfrac { 100,000 }{ { \left( 1+\cfrac { 0.075 }{ 2 } \right) }^{ 4 } } \\ & =101,003.01 \end{align*} $$
If the spot rates are each increased by 5 basis points (0.05%) so that the six-month spot rate is 6.05%, the one-year spot rate is 6.55%, and so on, the price of the bond is USD 100,911.18 calculated as:
$$ =4000\left( \cfrac { 1 }{ 1.02975 } +\cfrac { 1 }{ { \left( 1.03225 \right) }^{ 2 } } +\cfrac { 1 }{ { \left( 1.03475 \right) }^{ 3 } } +\cfrac { 1 }{ { \left( 1.03725 \right) }^{ 4 } } \right) +\cfrac { 100,000 }{ { \left( 1.03725 \right) }^{ 4 } } =101,094.96 $$
So,
$$ \begin{align*} \text{C} & =\cfrac { 1 }{ \text{P} } \left[ \cfrac { { \text{P} }^{ + }+{ \text{P} }^{ – }-2\text{P} }{ { \left( \Delta \text{r} \right) }^{ 2 } } \right] \\ & =\cfrac { 1 }{ 101,003.01 } \left[ \cfrac { 100,911.18+101,094.96-2\times 101,003.01 }{ { \left( 0.0005 \right) }^{ 2 } } \right] \\ & =4.752 \end{align*} $$
We now need to consider a group of instruments (such bonds) where we need to compute the interest-rate sensitivity measures we have been discussing.
The DV01 of a portfolio is simply the sum of individual DV01 of instruments in the portfolio.
For instance, if a bank has four positions whose DV01s are 9, 10, 12, and 13 (in USD millions), then the DV01 for the portfolio is 44 (=9+10+12+13).
Portfolio duration can be calculated as the weighted sum of the individual durations. The weight attached to each security is equal to its value as a percentage of total portfolio value.
$$ \text{Portfolio duration} =\sum _{ \text{j}=1 }^{ \text{k} }{ { { \text{w} }_{ \text{j} } { \text{D} }_{ \text{j} } } } $$
Where:
\({ \text{D} }_{ \text{j} }\) = duration of the bond j
\({ \text{w} }_{ \text{j} }\) = market value of the bond j divided by total portfolio market value
k = number of bonds in the portfolio
For instance, consider a portfolio consisting of four instruments with values (in USD millions) of 8, 13, 15 and 18, and respective effective durations are eight, seven, six, and four. The effective duration for the portfolio is given by:
$$ \begin{align*} \text{D}_{ \text{Eff} } & =\cfrac { 8 }{ 8+13+15+18 } \times 8+\cfrac { 13 }{ 8+13+15+18 } \times 7+\cfrac { 15 }{ 8+13+15+18 } \times 6+\cfrac { 18 }{ 8+13+15+18 }\times 4\\ & =1.1852+1.6852+1.6667+1.3333=5.87 \end{align*} $$
The effective portfolio duration is used to determine the impact of the small parallel shift of the term structure of the interest rates. Similar computations can be used in yield-based durations.
Portfolio convexity is computed using a similar approach. It’s defined as the value-weighted average of the individual bond convexities making up the portfolio.
$$ \text{Portfolio convexity} =\sum _{ \text{j}=1 }^{ \text{k} }{ { { \text{w} }_{ \text{j} } { \text{C} }_{ \text{j} } } } $$
Hedging using effective duration analogous to that of DV01. Now denote the duration of investment by \(\text D_{\text V}\), and its investment value by V. On the other hand, denote the effective duration of a bond by \(\text D_{\text B}\) and its value by P. By the definition of effective duration,
$$ \Delta \text{V}=-V{\text{D}}_{V}\Delta \text{r} $$
and
$$ \Delta \text{V}=-V{\text{D}}_{B}\Delta \text{r} $$
Where \(\Delta \text{r}\) is the size of a small parallel shift in the term structure. These small parallel shifts are hedged against if:
$$ \begin{align*} -\text{V}{\text{D}}_{\text{V}}\Delta \text{r}-\text{P}{\text{D}}_{\text{B}}\Delta \text{r}&=0 \\ \Rightarrow\Delta \text{r}\left(-\text{V}{\text{D}}_{\text{V}}-\text{P}{\text{D}}_{\text{B}}\right)&=0 \\ \therefore -\text{V}{\text{D}}_{\text{V}}-\text{P}{\text{D}}_{\text{B}}&=0 \end{align*}$$
If we make P the subject, the position required in the bond is:
$$ {\text{P}}=\cfrac{\text{V}{\text{D}}_{\text{V}}}{{\text{D}}_{\text{B}}} $$
A bank has a position of USD 12 million with an effective duration of 5 and a bond with an effective duration of 6. How will the bank hedge against its position?
The position required is given by:
$$ \begin{align*} {\text{P}} & =-\cfrac{\text{V}{\text{D}}_{\text{V}}}{{\text{D}}_{\text{B}}} \\ & =-\cfrac{5\times12}{6}=-10 \end{align*} $$
Therefore, the bank should short bonds worth 10 million to hedge against its position. This is true because:
$$ \Delta \text{V}=-12\times5\times\Delta \text{r}=-60\Delta \text{r} $$
and
$$ \begin{align*} \Delta \text{P} & =-10\times6\times\Delta \text{r}=60\Delta \text{r} \\ \Rightarrow\Delta \text{V} +\Delta \text{P} & =-60\Delta \text{r}+60\Delta \text{r}=0 \end{align*} $$
Hedging based on both duration and convexity is a complex undertaking where we are trying to reduce both the effective duration and convexity to zero. We need two bonds. Define:
\({\text{P}}_{1}\) = value of the first bond
\({\text{D}}_{1}\) = duration of the first bond
\({\text{C}}_{1}\) = convexity of the first bond
\({\text{P}}_{2}\) = value of the second bond
\({\text{D}}_{2}\) = duration of the second bond
\({\text{C}}_{2}\) = convexity of the second bond
Also, define
V = value of the position to be hedged
\({\text{P}}_{\text{V}}\) = duration of the position to be hedged
\({\text{C}}_{\text{V}}\) = convexity of the position to be hedged
Now by the definition of approximating the price change using a combination of the duration and convexity we have:
$$ \begin{align*}\Delta \text{V}&=-\text{V}{ \text{D} }_{ \text{V} }\Delta \text{r}+\cfrac { 1 }{ 2 } \text{V}{ \text{C} }_{ \text{V} }{ \left( \Delta \text{r} \right) }^{ 2 } \\ \Delta { \text{P} }_{ 1 }&=-{ { \text{P} }_{ 1 }\text{D} }_{ 1 }\Delta \text{r}+\cfrac { 1 }{ 2 } { { \text{P} }_{ 1 }\text{C} }_{ 1 }{ \left( \Delta \text{r} \right) }^{ 2 } \end{align*}$$
and
$$ \Delta { \text{P} }_{ 2 }=-{ { \text{P} }_{ 2 }\text{D} }_{ 2 }\Delta \text{r}+\cfrac { 1 }{ 2 } { { \text{P} }_{ 2 }\text{C} }_{ 2 }{ \left( \Delta \text{r} \right) }^{ 2 } $$
If we make both the duration and convexity to be zero, we have:
$$ -\text{V}{ \text{D} }_{ \text{V} }-{ { \text{P} }_{ 1 }\text{D} }_{ 1 }-{ { \text{P} }_{ 2 }\text{D} }_{ 2 }=0 $$
Also,
$$ \text{V}{ \text{C} }_{ \text{V} }+{ { \text{P} }_{ 1 }\text{C} }_{ 1 }+{ { \text{P} }_{ 2 }\text{C} }_{ 2 }=0 $$
These equations must be satisfied for a position to be hedged.
A bank has a position of USD 12 million with an effective duration of 5 and a convexity of 9. The bank wishes to hedge its position with two bonds where the first bond has an effective duration of 6 and a convexity of 9. The second bond has a duration of 4 and a convexity of 7. How will the bank hedge against its position?
We know that a position is hedged against if the following equations are satisfied:
$$ \begin{align*}-{\text{V}}{\text{D}}_{\text{V}}-{\text{P}}_{1}{\text{D}}_{1}-{\text{P}}_{2}{\text{D}}_{2}&=0 \\ {\text{V}}{\text{C}}_{\text{V}}+{\text{P}}_{1}{\text{C}}_{1}+{\text{P}}_{2}{\text{C}}_{2}&=0 \end{align*}$$
Therefore, we have \(\text{V}=12, {\text{D}}_{\text{V}}=5, \text{ and } {\text{ C}}_{\text{V}}=9. \text{For the bonds we have } {\text{C}}_{1}=9,{\text{D}}_{1}=6 \text{ also} {\text{ C}}_{2}=7,{\text{D}}_{2}=4\) so that:
$$ \begin{align*}{60}+{6\text{P}}_{1}+{4\text{P}}_{2}&=0 \\ {108}+{9\text{P}}_{1}+{7\text{P}}_{2}&=0 \end{align*}$$
Solving the above equation simultaneously, we get:
$$ {\text{P}}_{1}=2 \text{ and } {\text{P}}_{2}=-18 $$
Therefore, for the bank to hedge its position, it must take a long position of USD 2 in the first bond and a short position of USD 18 million in the second bond. In other words, by combining these positions in bonds, there is no duration or convexity exposure, and thus the bank is hedged against large parallel shifts in the term structure though it will be exposed to non-parallel shifts.
A barbell is an investment strategy applicable to fixed-income securities whereby half the portfolio is made up of long-term bonds and the other half of short-term bonds. On the other hand, a bullet strategy is an investment strategy where the investor buys bonds concentrated only in the intermediate maturity range.
Given the prices, coupon rates, maturities, yields, durations, and convexities of a set of bonds, it is possible to construct a barbell portfolio with the same cost and duration as the bullet portfolio. This involves determining the proportion of each security in the Barbell that should be bought, such that their total value equals that of the bullet.
Consider the following three bonds:
$$ \begin{array}{c|c|c|c} \textbf{Bonds} & \textbf{Bond Value} & \textbf{Effective Duration} & \textbf{Effective Convexity} \\ \hline \text{2-year, 3% coupon} & {88.90} & {4.567} & {21.23} \\ \hline \text{5-year, 5% coupon} & {99.80} &{7.767} & {78.90} \\ \hline \text{10-year, 7% coupon} & {120.45} &{13.43} & {180.56} \\ \end{array} $$
Assume that the term structure of the interest rates is flat at 5%, compounded semiannually. Note that this means that the yield on all instruments is 5%.
Now, assume that an investor wants a portfolio with a duration of 7.767. The investor can either buy a 5-year, 5% coupon (bullet investment) or build a portfolio of other two bonds to have the desired duration of 7.767 (barbell investment).
If the investor wishes to construct a bond from the other two bonds, denote:
Thus, the duration of the bond is
$$ \begin{align*} 4.567\alpha +13.43(1-\alpha ) & =7.767 \\ \Rightarrow \alpha & =0.6389 \end{align*} $$
Therefore, the investor can create a bond with a duration of 7.767 by either investing all his money in a 5-year coupon bond, or invest 63.89% of his funds into the 2-coupon bond, and 36.11% of his funds in the 10-year coupon bond.
Note that the portfolios have equal duration but different convexities. The convexity of the 5-year, 5% coupon bond is 78.90. For the portfolio consisting of 2-year, 3% coupon, and 10-year, 7% coupon bonds, the convexity is given by 78.8088 (=0.6389×21.3+0.3611×180.56) which is better than investing in one bond only.
An arbitrage opportunity can occur if one invests an amount in the barbell portfolio and short the same amount of the bullet portfolio. The arbitrage opportunity is possible if the movement in the term structure is parallel (which is not always true). Typically, the bullet investment is profitable for many non-parallel movements of the term structure as compared to the barbell investment. Most of the models are constructed in such a way there are no arbitrage opportunities to the investors.
Note: Sometimes, the bullet and Barbell have the same duration, but they will have different convexities.
Practice Question
The price of a 3-year bond is USD 10,000. The DV01 of the bond is 50. What is the estimated bond price change if all rates increase by five basis points?
- 25
- 5
- 250
- 50
The correct answer is C.
Recall that when the change in all rates is measured in basis points, the effective duration is equivalent to DV01 divided by the bond price. Therefore, in this case, the effective duration is given by:
$$ {\text{D}}=-\cfrac{50}{10,000}=-0.005=-50 $$
(Note: We measure the effective duration in decimal, i.e., per 10,000 basis points.)
The estimated price change using effective duration is given by:
$$ \begin{align*} \Delta {\text{P}} & =-\text{DP}\Delta {\text{r}} \\ & =-50\times10,000\times-0.0005=\text{USD } 250\end{align*} $$
(Note: 5 basis points = 0.05% = 0.0005.)