Common Univariate Random Variables
After completing this reading, you should be able to: Distinguish the key properties... Read More
After completing this reading, you should be able to:
A day count convention dictates how interest accrues over time in a variety of financial instruments, including bonds, swaps, and loans. It determines how interest is calculated at the end of each period. It’s usually expressed as a fraction \(\frac{ A }{ B }\). \(A\) defines the way in which the number of days between the two days is calculated, usually a notional or 30. \(B\) defines the way in which the total number of days in the reference period is measured, usually 360 or 365.
$$ \text { Accrued interest }=\text { Coupon }\times \frac { \text { Number of days between dates } }{ \text { Number of days in the reference period } } $$
The actual/actual convention means that the accrued interest is based on the ratio of the actual days elapsed to the actual number of days in the period between coupon payments. For example, suppose we have a bond paying a coupon rate of 10% per annum on a principal of $100 on March 1st and September 1st. This implies a coupon of $5 on each of these dates. If we want to compute the accrued interest as of May 31st, we will have to determine the actual number of days between May 31st and the last coupon date, i.e., March 1st. That’s 91 days (= 30 + 30 + 31). The reference period, March 1st to Sept 1st, has 184 actual days. Thus,
$$ \text { Accrued interest }=\frac { 91 }{ 184 } \times $5 $$
The actual/actual is used for Treasury bonds.
The 30/360 convention follows the same logic but assumes all months have exactly 30 days. It’s used for corporate and municipal bonds.
Based on the 30/360 convention, the above example will give us:
$$ \text { Accrued interest }=\frac { 89 }{ 180 } \times $5 =2.4722$$
89 days is obtained by adding 29+30+30 (number of days between March 1st and May 31st). The reference period, March 1st to September 1st, has 180 days(= 29 + 30+ 30+ 30+ 30+ 30+ 1, in March, April, May, June, July, August, and September, respectively).
The actual/360 convention is used for money market instruments, e.g., T-bills, commercial paper, and certificates of deposit. Interests of money market instruments are expressed per year. Suppose that a money market instrument earns an interest of 5% expressed on an actual/360 basis, the accrued interest will be:
$$ \text { Accrued interest }=\frac{ 365 }{ 360 } \times $5 $$
The dirty price of a bond – also known as the cash price – is the price that includes the present value of all of the bond’s cash flows, including the interest accruing on the next coupon payment date. It’s the price the issuer of the bond must be paid by the investor in order to dispense with the bond. The dirty price is comprised of the quoted price and accrued interest.
A bond quoted at 102–20 has accrued $2.54 in interest over the last six months. Determine the dirty price of the bond.
$$ \text { Dirty price }=\text { Quoted price }+\text { Accrued interest }=102+\frac { 20 }{ 32 } +2.54=$105.165 $$
The clean price of a bond is the price that excludes the interest that has accrued since the most recent coupon payment. It’s also known as the quoted price.
$$ \text { Clean price }=\text { Dirty price }–\text { Accrued interest }$$
Like other money market instruments, T-bills are issued at a discount to par value on an actual/360-day count basis. The quoted price is, in fact, the discount rate. If \(P\) is the quoted price and \(Y\) is the corresponding cash price per USD 100 of face value, then the quoted price, \(P\), can be expressed as:
$$ P=\frac { 360 }{ n } \left( 100-Y \right) $$
Alternatively, you might be asked to compute a T-bill’s cash price, in which case you should just make \(Y\) the subject of the formula:
$$ Y=100-\frac { Pn }{ 360 } $$
A 120-day treasury bill with a cash price of 99 would have a quoted price of:
$$ P=\frac { 360 }{ 120 } \left( 100-99 \right) = 3 $$
Deliverable securities for T-Bond futures contracts are bonds with remaining terms to maturity of 15 years or more. The cash received by the short position in a T-bond futures contract is given by:
$$ \text { Cash received }=\left( QFP\times CF \right) +AI $$
Where:
\(QFP\) = quoted futures price/settlement price
\(CF\) = conversion factor
\(AI\) = accrued interest since the last coupon date on the bond delivered
The conversion factor is given by:
$$ CF=\frac { \text { Discounted bond price }-\text { Accrued interest } }{ \text { Face value } } $$
For instance, if a bond has a present value of $125, accrued interest of $5, and $100 face value, then:
$$ CF=\frac { 125-5 }{ 100 } =1.20 $$
Conversion factors for different bonds are issued on a daily basis by the Chicago Board of Trade. A conversion factor is actually the approximate decimal price at which $1 par of a bond would trade if all interest rates are 6% compounded semi-annually.
Note that the cost of delivering a bond or note is
$$\text { Market Price }- \text { Price Received }$$
Obviously, the short-position party will choose the bond with the lowest cost to deliver it to the long-position party in line with contractual specifications. Such a bond is referred to as the cheapest to deliver (CTD). Determining the CTB bond is necessitated by a discrepancy between the market price of a security and the conversion factor used to determine the value of the security being delivered. Thus, picking one bond for delivery over another can be advantageous to the short position.
We have seen earlier that the price received for a bond is
$$\text{Cash received} = (\text{QFP} × \text{CF}) + \text{AI}$$
Where \(QFP\) is the quoted futures price/settlement price, \(CF\) is the conversion factor, and \(AI\) is the accrued interest.
The Cash market price of the bond is
$$\text{Quoted Price}+\text{Accrued Interest}$$
The cheapest to deliver bond is the one for which
$$\text{Quoted Price} – \text{Settlement Price} × \text{Conversion Factor}$$
is the least.
Note that Settlement price = Quoted futures price, and it should not be confused with the quoted price, which is just the current bond price.
CTB calculations are relevant in all cases where multiple financial instruments can satisfy the contract.
A number of factors can determine the cheapest to deliver bond. For example, if the bond’s interest rates are greater than 6 %, then bonds with low coupons and long maturity tend to be the cheapest to deliver. On the other hand, if the bond’s interest rates are less than 6 %, then bonds with high coupons and short maturity tend to be the cheapest to deliver.
An upward-sloping yield curve favors long-maturity bonds. On the other hand, a downward-sloping yield curve favors short-maturity bonds.
The theoretical futures price for a Treasury bond futures, \({ F }\), is given by:
$$ { F }=\left( { S }-I \right)(1+r)^{ T} $$
Where:
\({ S }\)=spot price of the bond
\(I\)=present value of cash flows, i.e., coupons
\(r\)=risk-free rate of interest
\(T\)=time to maturity
When \(r\) is expressed with continuous compounding, the above formula becomes
$$ { F }=\left( { S }-I \right) { e }^{ rT } $$
Under the terms of a futures contract, a bond will be delivered in 250 days. Assume that the last coupon of the bond was paid 40 days, and the next coupon will be paid in 143 days. If the risk-free rate is 5% with continuous compounding and the bond pays a coupon of 8% compounded semi-annually, what is the dirty futures price of the bond if the clean price is USD 107.00 and the conversion factor is 1.0400?
We can derive the bond’s spot price from the futures price formula.
We know that,
$$ F=(S−I)e^{ rT } $$
Thus,
$$S=107.00+(\frac{40}{183})×4 = 107.8743$$
since the next coupon is $4 per $100 face value and 40 of the 183 days between coupon payments have passed.
$$ \begin{align*} I &= 4e^{ -0.05×\frac { 143 }{ 365 } } = 3.9224\\ T&=\frac{250}{365}=0.6849 \text { years} \\ \end{align*}$$
So,
$$ F=(107.8743-3.9224) e^{ 0.05×0.6849 } = 107.5734$$
If the coupon after the next one is paid in 300 days (50 days after delivery), the clean price can be obtained by subtracting the accrued interest from the dirty price:
$$\begin{align*} \text {Dirty price}&= 107. 5734\\ \text {Accrued interest}&= \frac { 107 }{ 157 } × 4 = 2.7261\\ \end{align*} $$
Where 157 is obtained by subtracting 143 (the last coupon payment date) from 300 (the date when the next coupon payment will be made); and
107 represents the number of days of the 157 days between payments that will have passed (50 days will be remaining to the next coupon payment).
$$\begin{align*} \text {Clean futures price}&=\text {Dirty price}–\text {Accrued interest}\\& = 107. 5734 – 2.7261 = 104.8473\end{align*} $$
To get an estimate price of the futures contract price, we divide the clean futures price by the conversion factor which was given in the question:
$$ \text {Futures price}=\frac { 104.8473 }{ 1.04 } =100.8147 $$
Eurodollars are U.S. dollars deposited in banks outside the United States. Eurodollar futures provide a valuable tool for hedging fluctuations in short-term U.S. dollar interest rates. These types of futures have a maturity term of 3 months and largely reflect market expectations for that period.
The final price of a Eurodollar futures contract is determined by LIBOR on the last trading day. Eurodollar futures contract settle in cash and are based on a Eurodollar deposit of $1million.
The minimum price change is one “tick,” which is equivalent to one interest rate basis point = 0.01 price points = $25 per contract.
$$ \text {Eurodollar futures price}=$10,000\left[ 100-\left( 0.25 \right) \left( 100-Z \right) \right] $$
Where \(Z\) = quoted price for a Eurodollar futures contract
For example, if the quoted price \(Z\) is 98.5, then:
$$ \text {Eurodollar futures price}=$10,000\left[ 100-\left( 0.25 \right) \left( 100-98.50 \right) \right] =$996,250 $$
The three-month forward LIBOR for each contract is \(100 – Z\). In practice, however, daily marking-to-market can result in differences between actual forward rates and those implied by fixtures contracts. To reduce this difference, we use a convexity adjustment:
$$ \text { Actual forward rate } =\text { Forward rate implied by futures }-\left( \frac { 1 }{ 2 } \times { \sigma }^{ 2 }\times { T }_{ 1 }\times { T }_{ 2 } \right) $$
Where:
\({ T }_{ 1 }\) = maturity on the futures contract
\({ T }_{ 2 }\) = time to the maturity of the rate underlying the contract (90 days)
\(\sigma\)= annual standard deviation of the change in the rate underlying the futures contract, or 90-day LIBOR
A duration-based hedge ratio is a hedge ratio constructed when interest rate futures contracts are used to hedge positions in an interest-dependent asset, usually bonds money market securities.
The number of futures contracts (\(N\)) required to hedge against a given change in yield, \(\left( \Delta y \right) \) is:
$$ N=-\frac { P\times DP }{ FC\times DF } $$
Where:
\(P\) = forward value of the fixed-income portfolio being hedged
\(DP\) = duration of the portfolio at the maturity date of the hedge
\(FC\) = futures contract price
\(DF\) = duration of the asset underlying the futures
The negative sign implies that the number of contracts taken up must be the opposite of the original position. If the investor is short of the portfolio, for example, they must long \(N\) contracts to produce a position with zero duration.
A pension fund has a $25 million portfolio of Treasury bonds with a portfolio duration of 6.1. The cheapest to deliver bond has a duration of 4.7. The six-month treasury bond futures price is $127,000. What is the number of futures contracts to fully hedge the portfolio?
$$ \begin{align*} N&=-\frac { P\times DP }{ FC\times DF }\\ &=-\frac { $25,000,000\times 6.1 }{ $127,000\times 4.7} = -255\\ \end{align*} $$
If yields rise over the next 6 months, it’s bad news for the portfolio as it will lose value. Suppose the new value is $23.5 million, then it’s good news in the futures market as the gains can be used to offset the spot market losses.
In fact, if the hedge is executed properly and the yield curve changes are parallel, then it is possible to gain $1.5 million in the derivatives market. The total portfolio value after the hedge is $25 million.
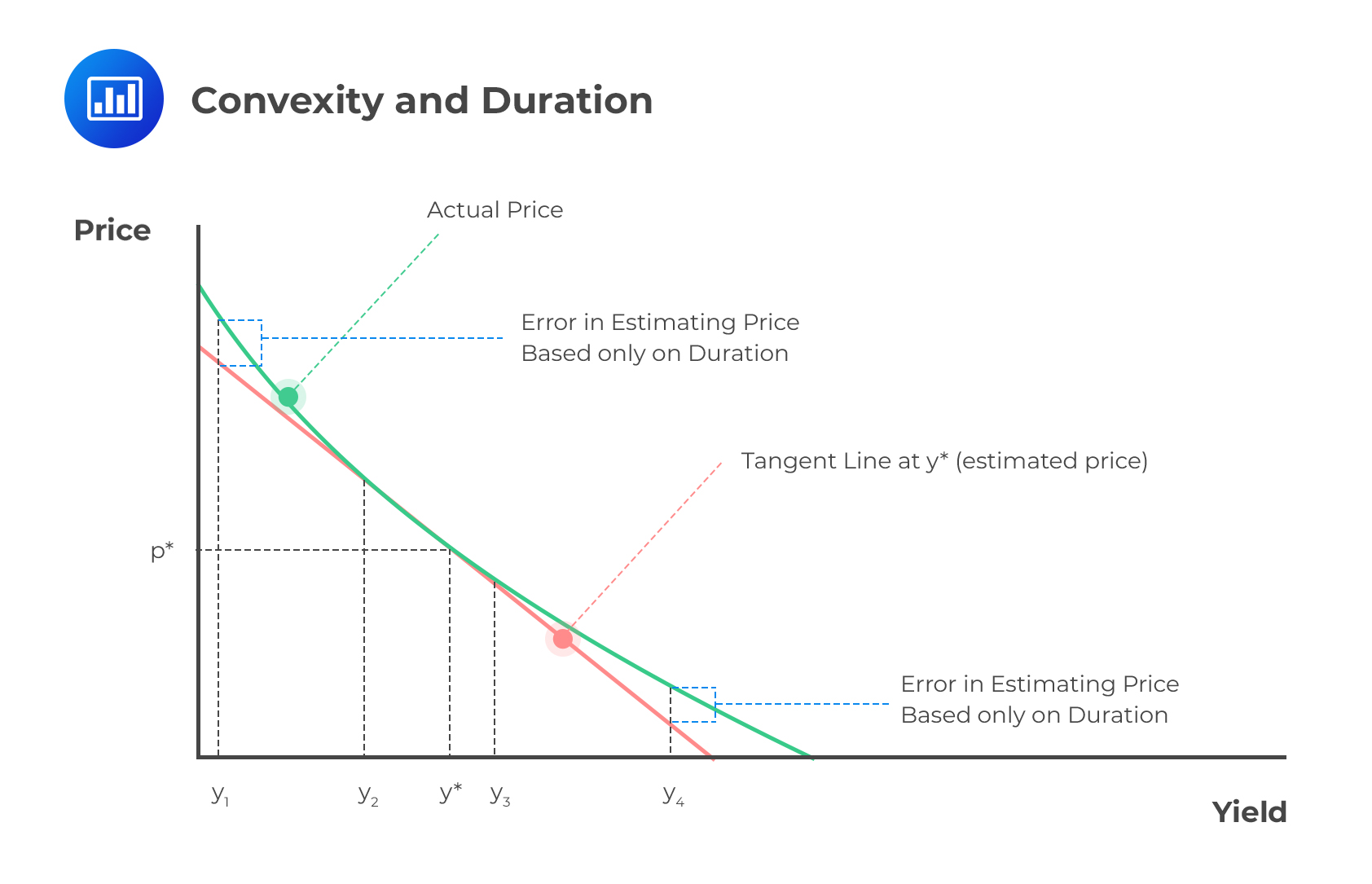
The major limitation of employing a duration-based hedging strategy has much to do with the fact that duration measures are only accurate for small changes in yield. For large changes in yield, the price/yield relationship is not linear but is actually convex. Thus, using the strategy in the face of large moves in yield will result in “underhedging.”
Practice Question
Alina Escobar is a junior derivatives analyst at the derivatives investment unit of a financial institution. The company holds a mid-day meeting where managers discuss investment strategies according to recent trends in the market. Escobar’s manager asked her to estimate the price of a March Eurodollar futures contract that is quoted as $94.25. Estimate the price that the firm will have to pay if the firm ultimately decides to invest in the March Eurodollar futures contract.
A. $942,500
B. $985,625
C. $991,750
D. $1,050,870
The correct answer is B.
Since the size of one Eurodollar contract is $1 million and the change of one basis point is 25, we will use the following formula to calculate the price of the Eurodollar futures contract:
$$ \text{Price of the Eurodollar} = 10,000 × [100 – 0.25 × (100 – 94.25)] = $985,625$$