Hypothesis Testing

Hypothesis testing involves testing an assumption regarding a population parameter. A null hypothesis is a condition believed not to be true. We reject the null hypothesis in the presence of enough evidence against it and accept the alternative hypothesis.

Hypothesis testing is performed on the estimated slope coefficients to establish if the independent variables make a significant contribution to explaining the variation in the dependent variable.

The t-statistic for testing the significance of the individual coefficients in a multiple regression model is calculated using the formula:

$$t=\frac{\widehat{b_{j}}-b_{H0}}{S_{\widehat{b_{j}}}}$$

Where:

• \(\widehat{b_{j}}\) = Estimated regression coefficient.
• \(b_{H0}\) = Hypothesized value.
• \(S_{\widehat{b_{j}}}\) The standard error of the estimated coefficient.

Note that the test statistic has \(n-k-1\) degrees of freedom, where \(k\) is the number of independent variables, and \(1\) is the intercept term.

A t-test tests the null hypothesis that the regression coefficient is equal to some hypothesized value against the alternative hypothesis that it is not.

\(H_0:b_j=v\) v.s \(H_{a}:b_{j}≠v\)

Where:

• \(v\) = Hypothesized value.

The following are the steps followed in hypothesis testing:

  i. Formulate hypothesis.

• For example, Null hypothesis, \(H_0: b_{j}=0\) vs Alternative hypothesis, \(H_{a}: b_{j}≠0\).

  ii. Determine the suitable test statistic.

$$t_{statistic}= \frac{\widehat{b_{j}}-b_{H0}}{S_{\widehat{b_{j}}}}$$

   iii. Specify the significance level.

• 5% significance level is commonly used.

   iv. Make the statistical decision.

• Reject the null hypothesis when the t-statistic is greater than the absolute value of the critical value of t.

Example: The Test of Significance for a Regression Coefficient

Consider the following multiple regression results of the price of USDX versur inflation rate and real interest rate.

$$\small{\begin{array}{l|c}\hline\textbf{Regression Statistics}\\ \hline\text{Multiple R} & 0.8264\\ \hline\text{R Square} & 0.6830\\ \hline\text{Adjusted R Square} & 0.5924\\ \hline\text{Standard Error} & 5.3537\\ \hline\text{Observations} & 10\\ \hline\end{array}}$$

$$\small{\begin{array}{l|c|c|c|c}{}& \textbf{Coefficients} & \textbf{Standard Error} & \textbf{t-statistic} & \textbf{P-value}\\ \hline\text{Intercept} & 81 & 7.9659 & 10.1296 & 0.0000\\ \hline\text{Inflation rates} & -276 & 233.0748 & -1.1833 & 0.2753\\ \hline\text{Real interest Rates} & 902 & 279.6949 & 3.2266 & 0.0145\\ \end{array}}$$

Test the statistical significance of the independent variable real rate of interest at the 5% significance level.

Solution

We are testing the hypothesis:

\(H_{0}\): Real Interest Rate=0 versus \(H_{a}\): Real Interest Rate ≠ 0.

The t-statistic is determined as:

$$t=\frac{\widehat{b_{j}}-b_{H0}}{S_{\widehat{b_{j}}}}$$

$$\begin{align*}t&=\frac{902-0}{279.6949}\\&=3.22\end{align*}$$

The 5% two-tailed critical t-value with \(10-2-1 = 7\) degrees of freedom is 2.3646.

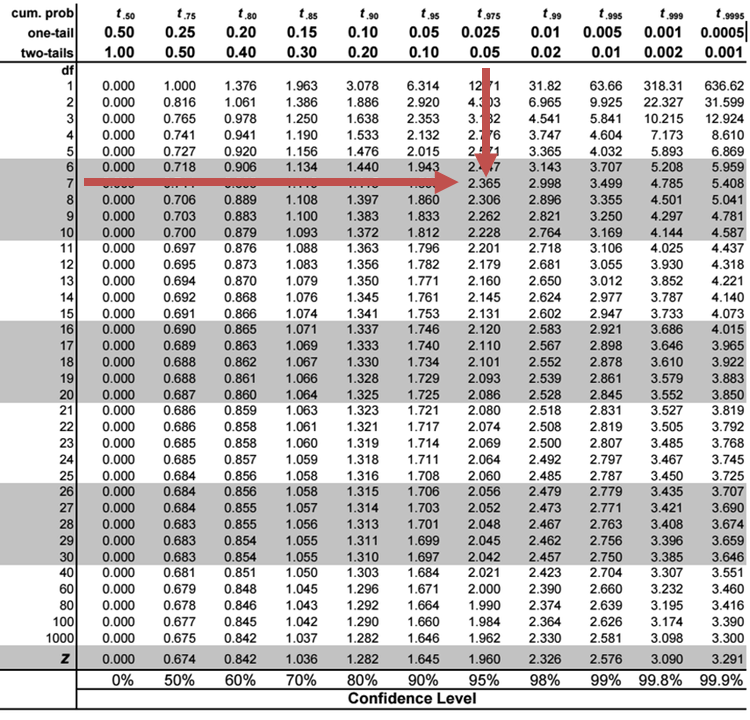
Since the t-statistic, \(3.22\), is greater than the critical value, \(2.365\), we reject the null hypothesis and conclude that the real interest rate regression coefficient is statistically significantly different from zero at the 5% significance level.

Question

Consider the following multiple regression results of the return on capital (ROC) vs. performance measures (profit margin (%), sales and debt ratio).

$$\small{\begin{array}{|l|c|}\hline\textbf{Regression Statistics}\\ \hline\text{Multiple R} & 0.7906\\ \hline\text{R Square} & 0.6251\\ \hline\text{Adjusted R Square} & 0.5715\\ \hline\text{Standard Error} & 1.1963\\ \hline\text{Observations} & 25\\ \hline\end{array}}$$

$$\small{\begin{array}{l|c|c|c|c|c}{}& \textbf{Coefficients} & \textbf{Standard Error} & \textbf{t Stat} & \textbf{P-value} \\ \hline\text{Intercept} & 8.6531 & 0.9174 & 9.4323 & 0.0000 \\ \hline \text{Sales} & 0.0009 & 0.0005 & 1.7644 & 0.0922\\ \hline\text{Debt ratio} & 0.0229 & 0.0165 & 1.3880 & 0.1797 \\ \hline\text{Profit Margin%} & 0.2996 & 0.0564 & 5.3146 & 0.0000\\ \end{array}}$$

Adil Suleman, CFA, wants to test whether \(b_{o}\) is different from zero. Assuming a 5% significance level, the hypothesis used and the result of the hypothesis test are most likely: 

$$\begin{array}{|l|l|l|} \hline
\text{A} & H_{0}:b_{0}= 0, vs. H_{a}: b_0≠0 &  {\text{Fail to reject the null hypothesis and conclude that}\\ b_0  \text{ is equal to zero.}}\\ \hline
\text{B} & H_{0}:b_{0}= 0, vs. H_{a}: b_0=0 &  {\text{Reject the null hypothesis and conclude that}\\ b_0  \text{ is equal to zero.}} \\ \hline
\text{C} & H_{0}:b_{0}= 0, vs. H_{a}: b_0≠0 & {\text{Reject the null hypothesis and conclude that}\\ b_0 \text{ is not equal to zero.}} \\ \hline
\end{array}$$

Solution

The correct answer is C.

The hypothesis will be structured as:

\(H_0:b_0\), v.s. \(H_a: b_0 ≠0\)

\(\text{t-statistic}= 9.4323\)

This is a two-tailed test: The critical t-value with 23 degrees of freedom at the 5% significance level is ±2.069.

Notice that the t-stat is greater than the upper critical value. This prompts the rejection of the null hypothesis and conclusion that  is significantly different from zero.

Reading 2: Multiple Regression

LOS 2 (c) Formulate a null and an alternative hypothesis about the population value of a regression coefficient, calculate the value of the test statistic, and determine whether to reject the null hypothesis at a given level of significance.