Binomial Option Valuation Model

One-Period Binomial Option Valuation Model

In the one-period binomial model, we start today (at time t=0) when the stock price is \(S_{0}\). Then, the stock price can either jump upwards or downwards over the one-period time interval to t=1. This is illustrated below:

$$S_1=\{\begin{align*}S_{0}u& , \text{if the stock price jumps up} \\S_{0}d& , \text{if the stock price jumps down}\end{align*}$$

This can be shown in the following binomial tree:

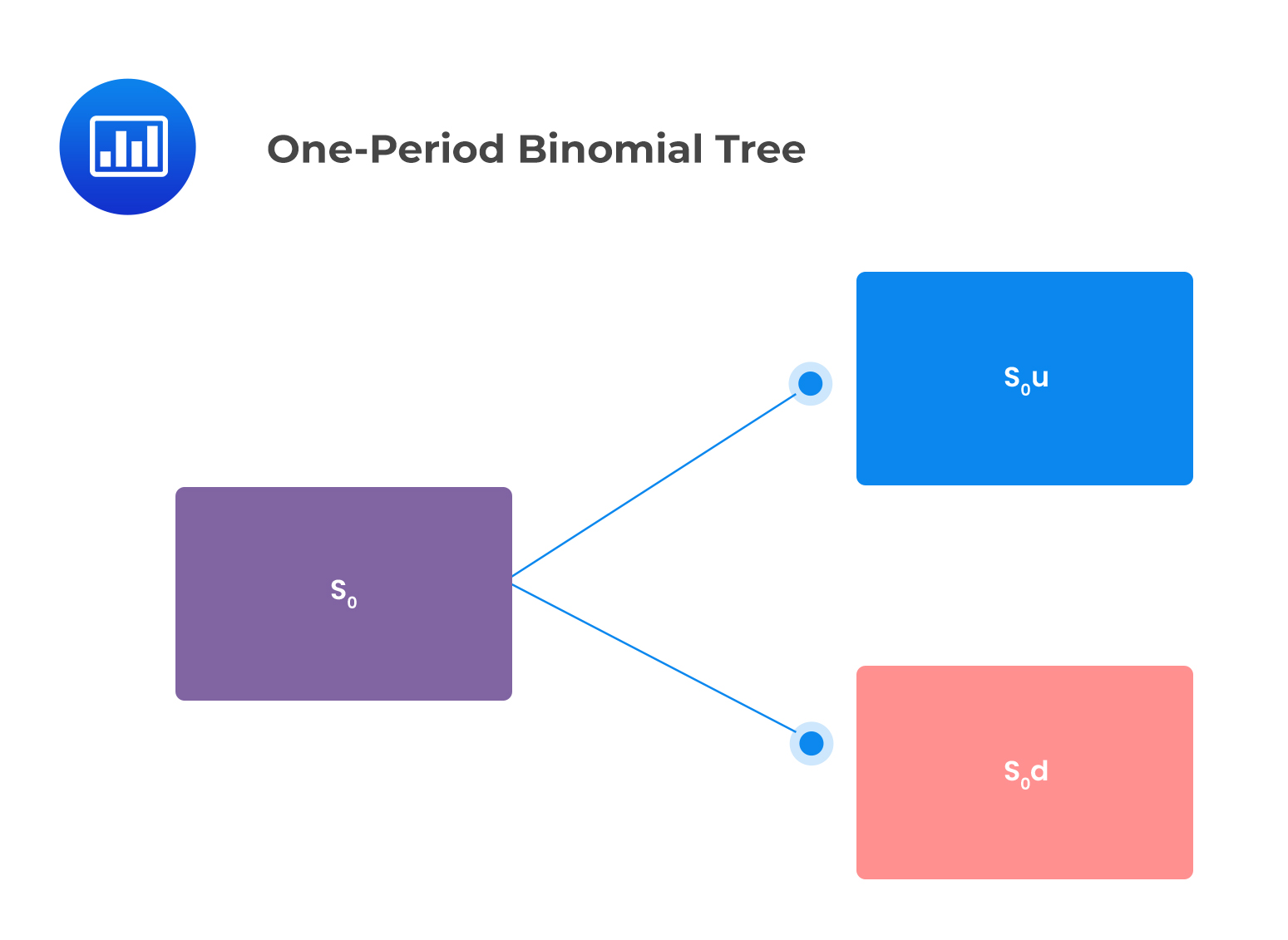Where:

$$u=\frac{S_{0}u}{S_{0}}$$

$$d=\frac{S_{0}d}{S_{0}}$$

One period Binomial option payoffs

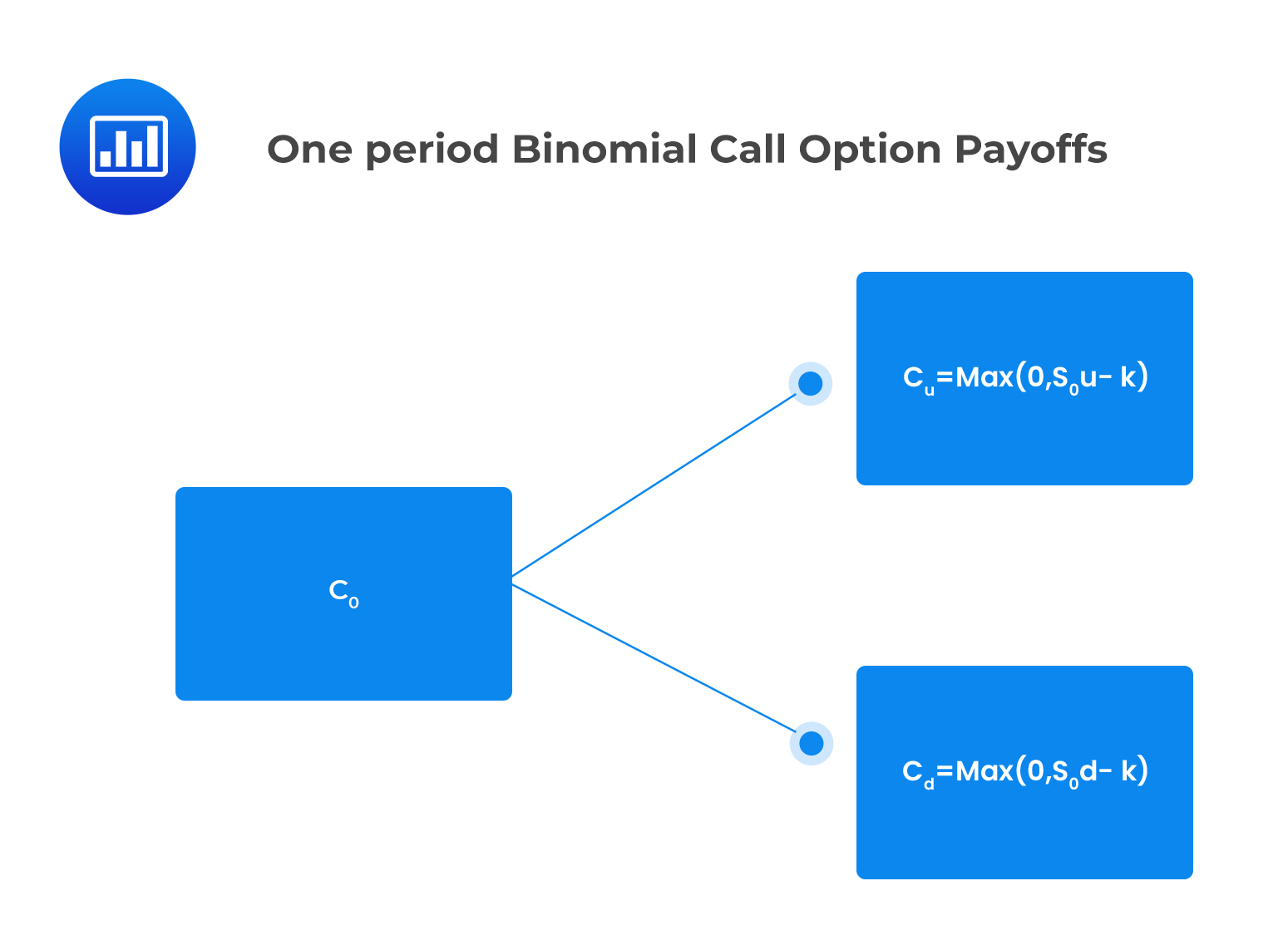
Consider a call option that pays \(c_{u}\) if the price of the underlying asset jumps up and  \(c_{d}\) if the price of the underlying asset jumps down.

The value of the call option at expiry is expressed as:

\(c_{u}=Max(0,S_{0}u-K)\), if the price of the underlying jumps up

and 

\(c_{d}=Max(0,S_{0}d-K), \)if the stock price jumps down

Where K is the strike price.

This is shown in the following binomial tree:

Similarly, the value of a put option at expiration is given by:

\(p_{u}=Max(0,K-S_{0}u)\), if the price of the underlying asset jumps up

and

\(p_{d}=Max(0, K- S_{0}d)\), if the price of the underlying asset jumps down.

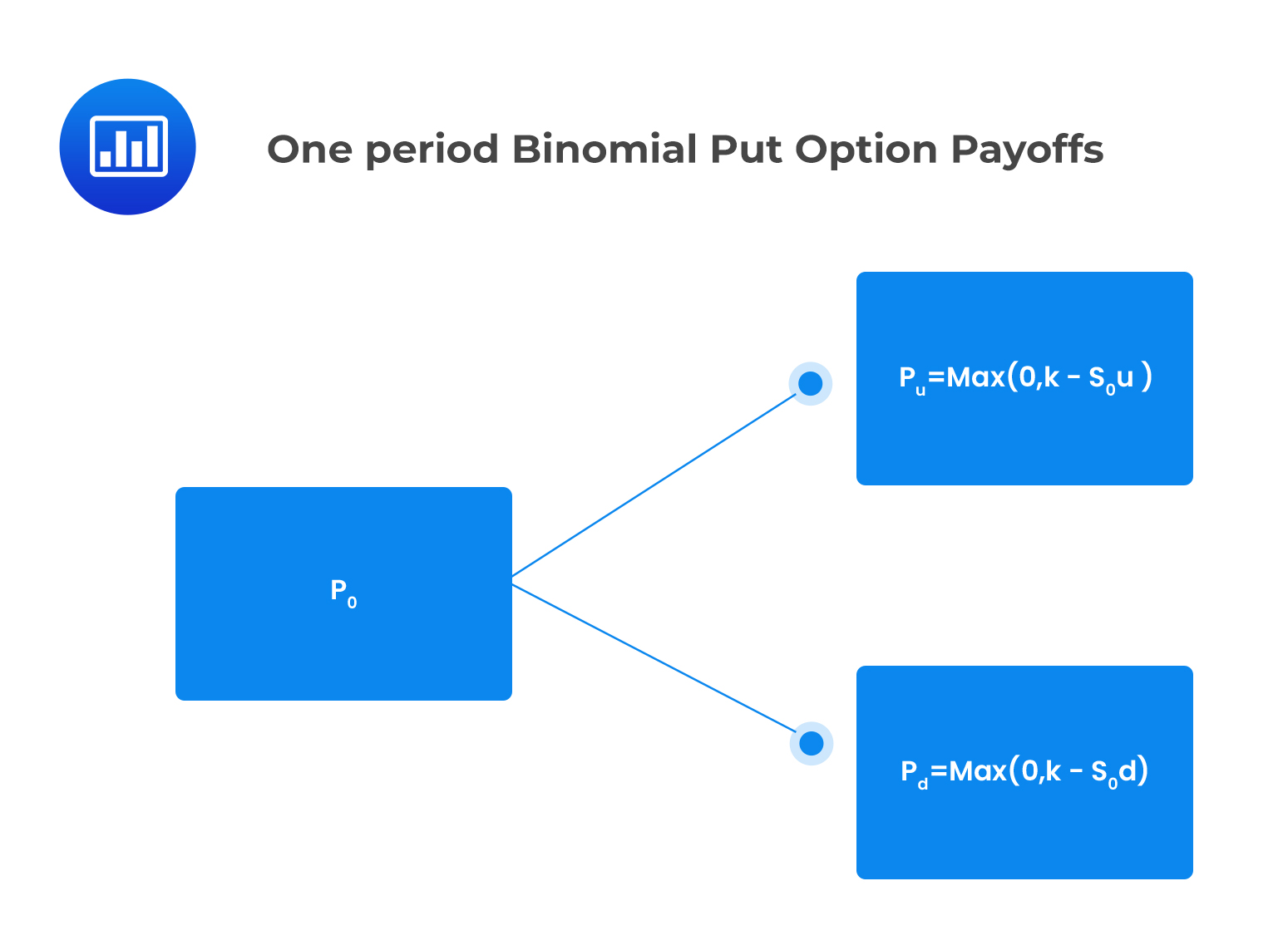One period Binomial option values

The initial values of call and put options with a one period to expiry are determined using the following formulas:

$$C_{0}=\frac{qc_{u}+(1-q)c_{d}}{1+r}$$

And

$$p_{0}=\frac{qp_{u}+(1-q)p_{d}}{1+r}$$

Where: 

$$q=\frac{(1+r)-d}{u-d}$$

Where: 

\(r\) is the risk-free rate for a single period.

\(q\) gives the risk-neutral probability of an upward move in price

\(1-q\) gives the risk-neutral probability of a downward move

Example: Calculating the price of an option using the one-period binomial option valuation model

Consider a European put option with a strike price of $50 on a stock whose initial price is $50. The risk-free rate of interest is 4%, the up-move factor u = 1.20, and the down move factor d =0.83. The price of the put option can be determined using the one-period binomial model as follows:

$$S_{0}u=50\times1.20=$60$$

$$S_{0}d=50\times0.83=$41.50$$

Recall that put payoff is given by:

\(p_{u}=\text{Max}(0, K-S_{0}u)\), if the price of the underlying asset jumps up

and 

\(p_{d}=\text{Max}(0, K-S_{0}d)\), if the price of the underlying asset jumps down.

$$p_{u}=Max(0,50-60)=$0$$

$$p_{d}=\text{Max}(0,60-41.50)=$18.50$$

The value of the put is then calculated using the formula: 

$$p_{0}=\frac{qp_{u}+(1-q)p_{d}}{1+r}$$

Where:

$$q=\frac{(1.04)-0.83}{1.20-0.83}=0.5676$$

$$p_{0}=\frac{0.5676\times$0+0.4324\times$18.50}{1.04}=$7.69$$

Two-Period Binomial Option Valuation Model

The one-period binomial model can be extended into a multi-period context. The two-period binomial lattice can be seen as three-one period binomial lattices as shown below:

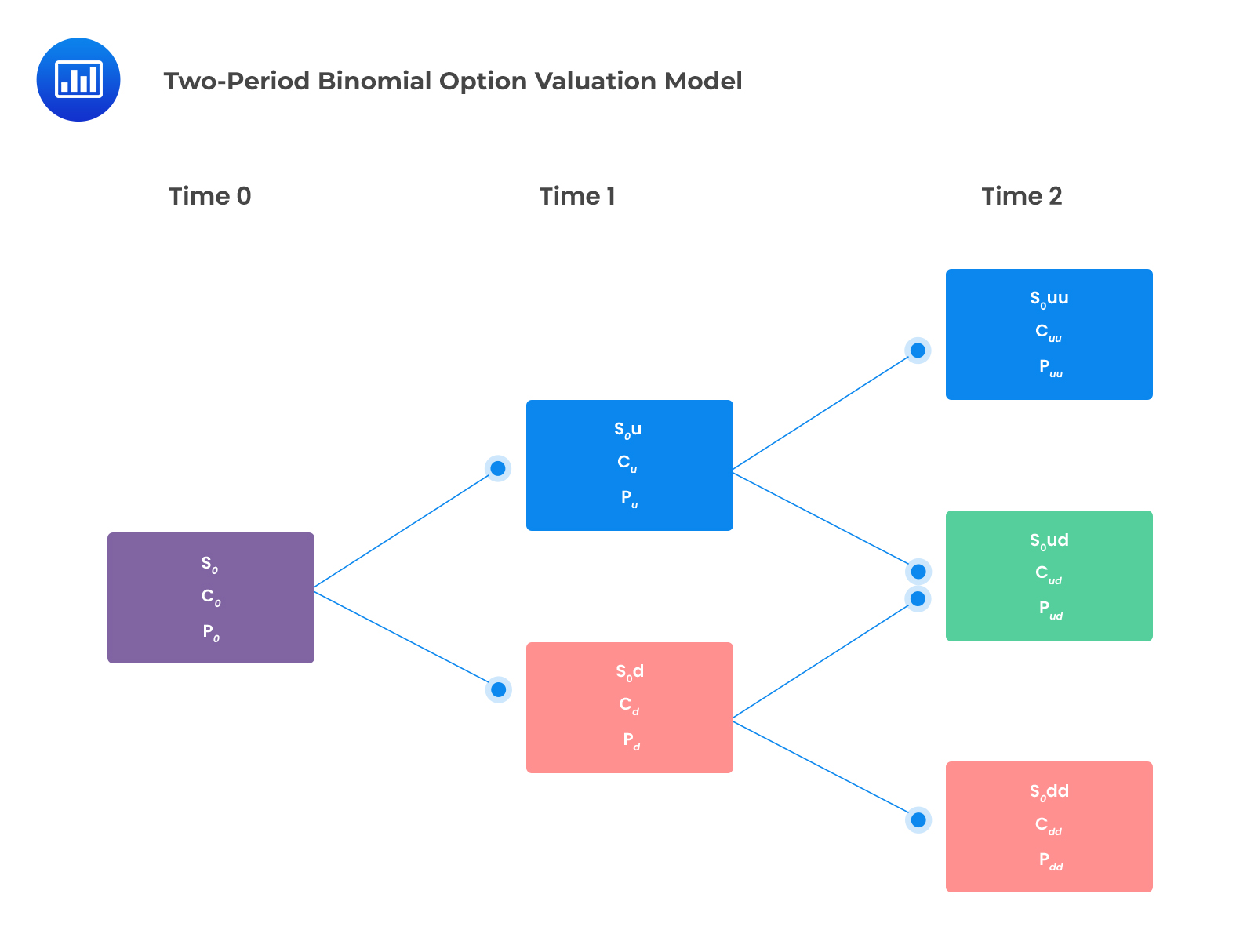The underlying asset can result in only three possible values:

\(S_{0}uu=\) When price moves up twice

\(S_{0}ud=\) When price either moves up then down or down then up

\(S_{0}dd=\) When price moves down twice

Call Payoffs

A call option under the two-period binomial option model will have three possible payoffs at expiry as follows:

$$C_{uu}=\text{max}(0, S_{0}u^{2}-K)$$

$$C_{ud}=Max(0,S_{0}ud-K)$$

$$C_{dd}=Max(0,S_{0}d^{2}-K)$$

Put Payoffs

Similar to a call option, a put option will have three possible payoffs:

$$p_{uu}=Max(o,K-S_{0}u^{2})$$

$$p_{ud}=Max(0,K-S_{0}ud)$$

$$p_{dd}=Max(0,K-S_{0}d^{2})$$

Option Values

A European call option’s value can be determined using the two-step binomial valuation model using the following formula.

$$c_{0}=\frac{q^{2}c_{uu}+2q(1-q)c_{ud}+(1-q)^{2}c_{dd}}{(1+r)^{2}}$$

The two-period European put value is given as:

$$p_{o}=\frac{q^{2}p_{uu}+2q(1-q)p_{ud}+(1-q)^{2}p_{dd}}{(1+r)^{2}}$$

These concepts will be explained more with examples in the sections that follow.

Question

Suppose that a one-year European call option has a strike price of £60. The underlying non-dividend-paying stock is currently trading at £60. Over one year, the stock price can either jump up to £90 or jump down to £50. The annual risk-free interest rate is 4%. Using a one-period binomial option valuation model, the price of the call option is closest to:

1. £2.44
2. £9.04
3. £15.64

Solution

The correct answer is B:

The payoff of a European call option at expiration is given by:

\(c_{u}=Max(0,S_{0}u-K)\), if the price of the underlying jumps up

and

\(c_{d}=Max(0,S_{0}d-K)\), if the stock price jumps down

$$u=\frac{90}{60}=1.5$$

$$d=\frac{50}{60}=0.83$$

$$c_{u}=Max(0,90-60)=£30$$

$$c_{d}=Max(0,50-60)=£0$$

The value of a call option is then calculated using the formula:

$$c_{0}=\frac{qc_{u}+(1-q)c_{d}}{1+r}$$

Where:

$$q=\frac{1.04-0.83}{1.5-0.83}=0.3134$$

$$c_{0}=\frac{0.3134\times£30+0.6866\times£0}{1.04}=£9.04$$

Reading 38: Valuation of Contingent Claims

LOS 38 (a): Describe and interpret the binomial option valuation model and its component terms