Multicollinearity

Multicollinearity occurs when two or more independent variables are significantly correlated to each other.

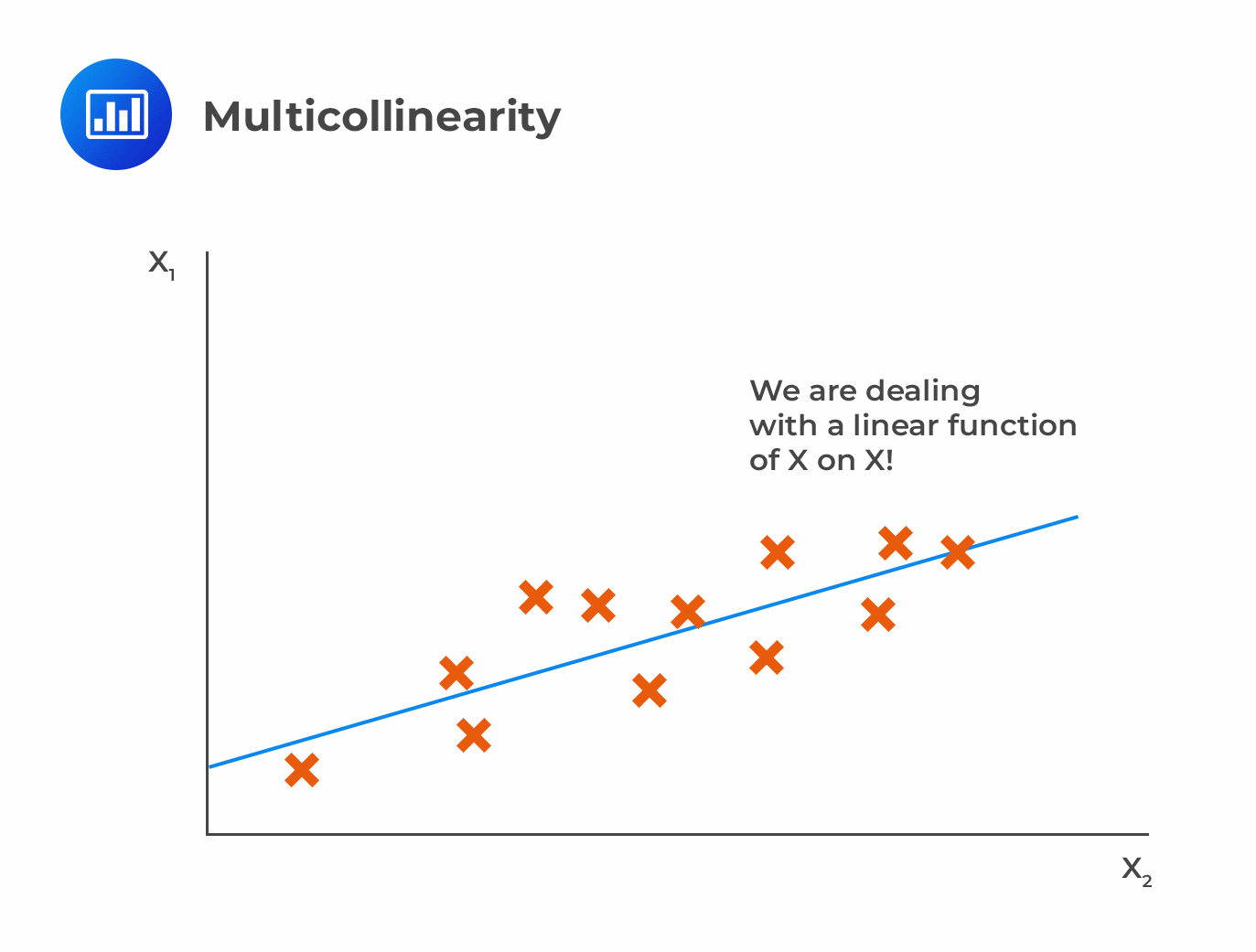It results from the violation of the multiple regression assumptions that there is no apparent linear relationship between two or more of the independent variables. Multicollinearity is common with financial data.

Effects of Multicollinearity

Multicollinearity does not alter the consistency of the regression estimates. However, it renders them imprecise and unreliable. Multicollinearity makes it nearly impossible to determine how the independent variables influence the dependent variable individually. This inflates the standard errors for the regression coefficients, increasing the possibility of Type II errors.

Detecting Multicollinearity

A high value of R² and a significant F-statistic that contradicts the t-test signals multicollinearity. The insignificant t-statistic implies that the standard errors are overestimated. In addition, a high correlation between independent variables indicates multicollinearity. It is important to note that a low correlation between independent variables does not imply the absence of multicollinearity.

Correcting Multicollinearity

The most common way to attenuate the problem of multicollinearity is to exclude some of the regression variables, provided that we do not omit relevant variables. However, it is hard to identify the variables that need to be eliminated. This is why stepwise regression is employed to systematically eliminate variables from the regression until multicollinearity is minimized.

Finally, we can summarize the problems in linear regression and their solutions as per the following table:

$$\small{\begin{array}{l|l|l}\textbf{Problem} & \textbf{Effect} & \textbf{Solution}\\ \hline\text{Heteroskedasticity} & \text{Incorrect standard errors} & \text{Use robust standard errors}\\ \hline\text{Serial correlation} & \text{Incorrect standard errors} & \text{Use robust standard errors}\\ \hline\text{Multicollinearity} & \text{High R-squared and low t-statistics} & \text{Eliminate one or more independent variables}\\ \hline{}& {}& \text{Stepwise regression}\\ \end{array}}$$

Question

The regression problem that will most likely increase the chances of making Type II errors is:

   A. Multicollinearity.

   B. Conditional heteroskedasticity.

   C. Positive serial correlation.

Solution

The correct answer is A.

Multicollinearity makes the standard errors of the slope coefficients to be artificially inflated. This increases the likelihood of incorrectly concluding that a variable is not statistically significant (Type II error).

B is incorrect. Conditional heteroskedasticity underestimates standard errors while the coefficient estimates remain unaffected. This inflates the t-statistics leading to the frequent rejection of the null hypothesis of no statistical significance. (Type I error).

C is incorrect. Positive serial correlation makes the ordinary least squares standard errors for the regression coefficients to underestimate the true standard errors. This inflates the estimated t-statistics, making them appear to be more significant than they really are. This increases Type I error.

Reading 2: Multiple Regression

LOS 2 (l) Describe multicollinearity and explain its causes and effects in regression analysis.