Autoregressive Models and Multiperiod ...
[vsw id=”-SilFtkpBK8″ source=”youtube” width=”611″ height=”344″ autoplay=”no”] The current-time values of a time series... Read More
Most quantitative stock selection models use a multifactor structure. For example, fundamental managers use multiple filters to screen stocks. The two multifactor equity portfolio strategies most commonly used to illustrate backtesting are benchmark (BM) factor portfolio and risk parity (RP) factor portfolio. The risk parity factor portfolio weighs factors based on their equal risk contribution, while the benchmark factor portfolio weighs many fundamental factors equally. These two approaches are used because they have objective weighting schemes, i.e., equal risk weights and equal weights.
To backtest the two portfolios, we will follow the three steps we discussed earlier.
We selected eight fundamental factors from well-known investment styles:
For each factor, a portfolio is formed by shorting the bottom 20% and buying the top 20% of stocks ranked by the factor. All stocks are weighted equally. It is evident that all factors have a positive return. Earnings yield, price momentum, and earnings revision had the highest returns, while debt or equity and earnings growth had the lowest returns.
The eight-factor portfolios will be combined by equal weight each to generate our benchmark portfolio. The performance of an equally weighted portfolio is in tune with the portfolios. Nevertheless, it can outperform them when more sophisticated techniques are used.
To construct our risk parity portfolio, we will weigh the eight portfolios equally based on their risk contribution. This is a popular way of constructing a portfolio that accounts for the correlation of returns among all factors and the volatility of each factor. The BM and RP portfolios are long-only; thus, the weight allocated to each factor portfolio is restricted to be non-negative.
The rolling method will be implemented twice, once for each portfolio, when backtesting a multi-factor strategy. We first create eight-factor portfolios monthly for the entire period and then split the factor portfolios into two. One will be a benchmark portfolio, and the other, the risk parity portfolio.
To avoid look-ahead bias, a second rolling-window procedure is conducted. A variance-covariance matrix is then developed using monthly data for the eight-factor portfolio. Once estimated, the covariance matrix is used to compute and optimize the weights for equal risk contribution for each eight-factor portfolio.
From the following image, we can see that the benchmark portfolio offers a higher cumulative return than the risk parity portfolio.
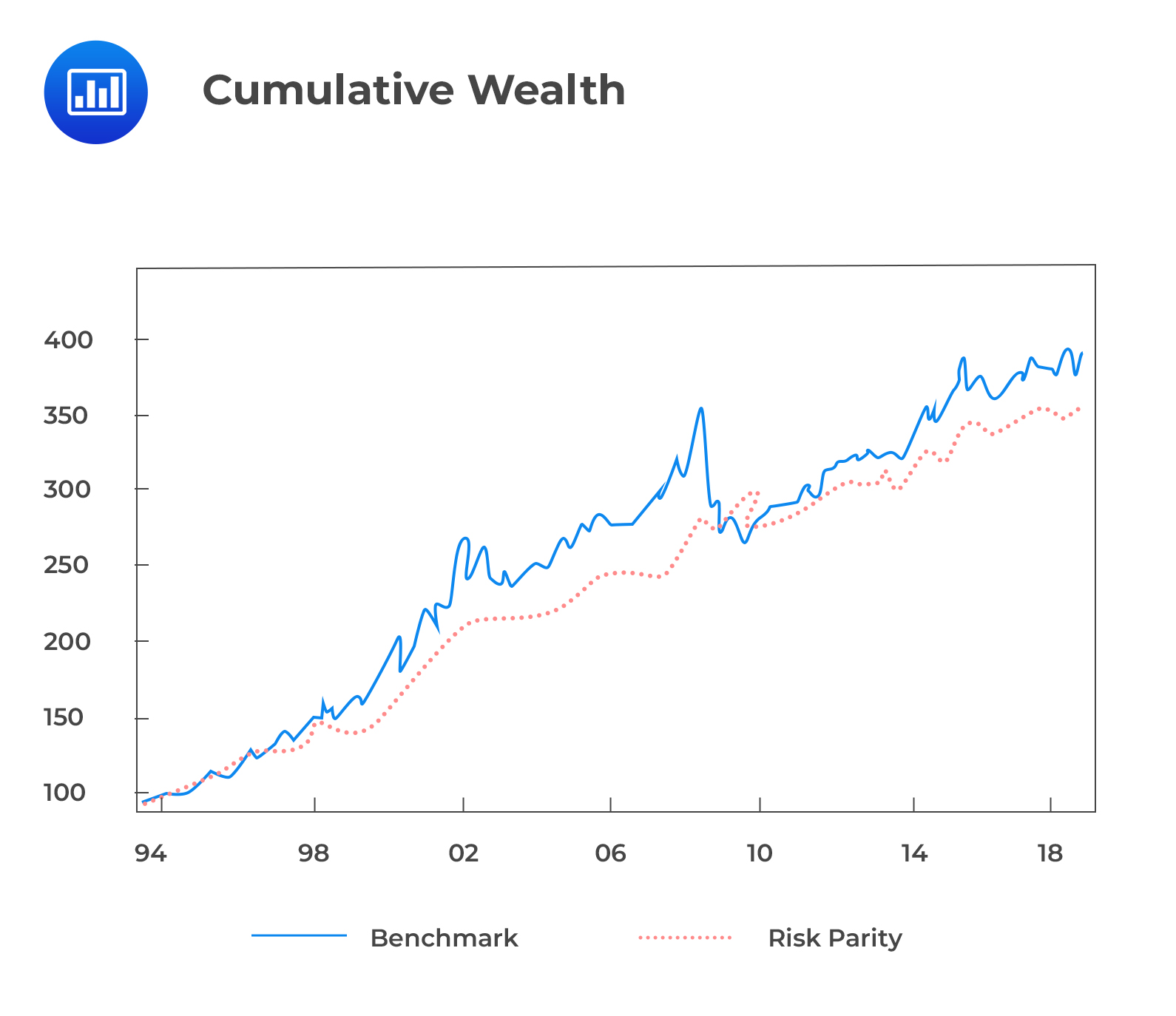 However, the next graph shows that the volatility of the benchmark portfolio is more than half that of the risk parity portfolio.
However, the next graph shows that the volatility of the benchmark portfolio is more than half that of the risk parity portfolio.
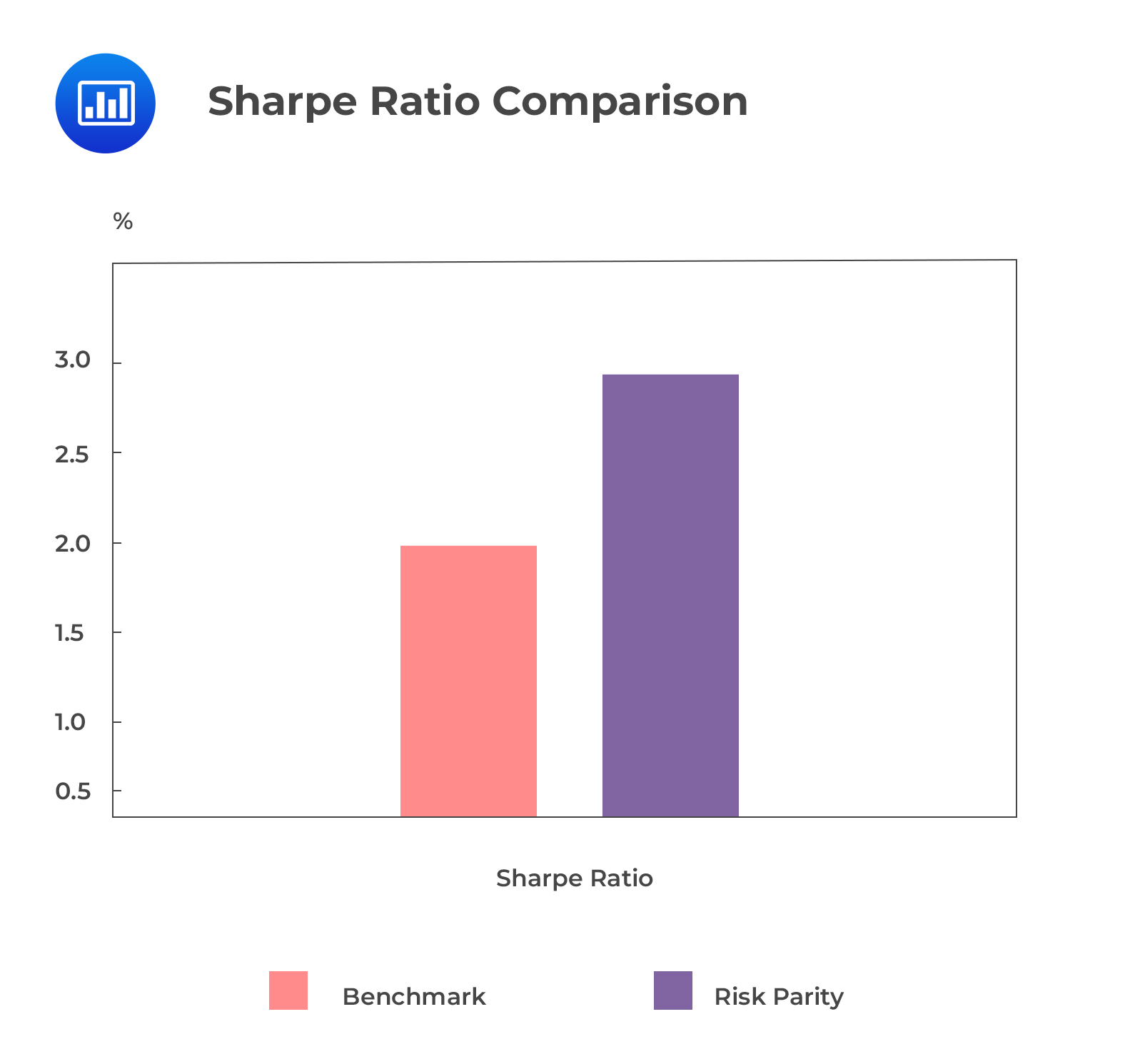
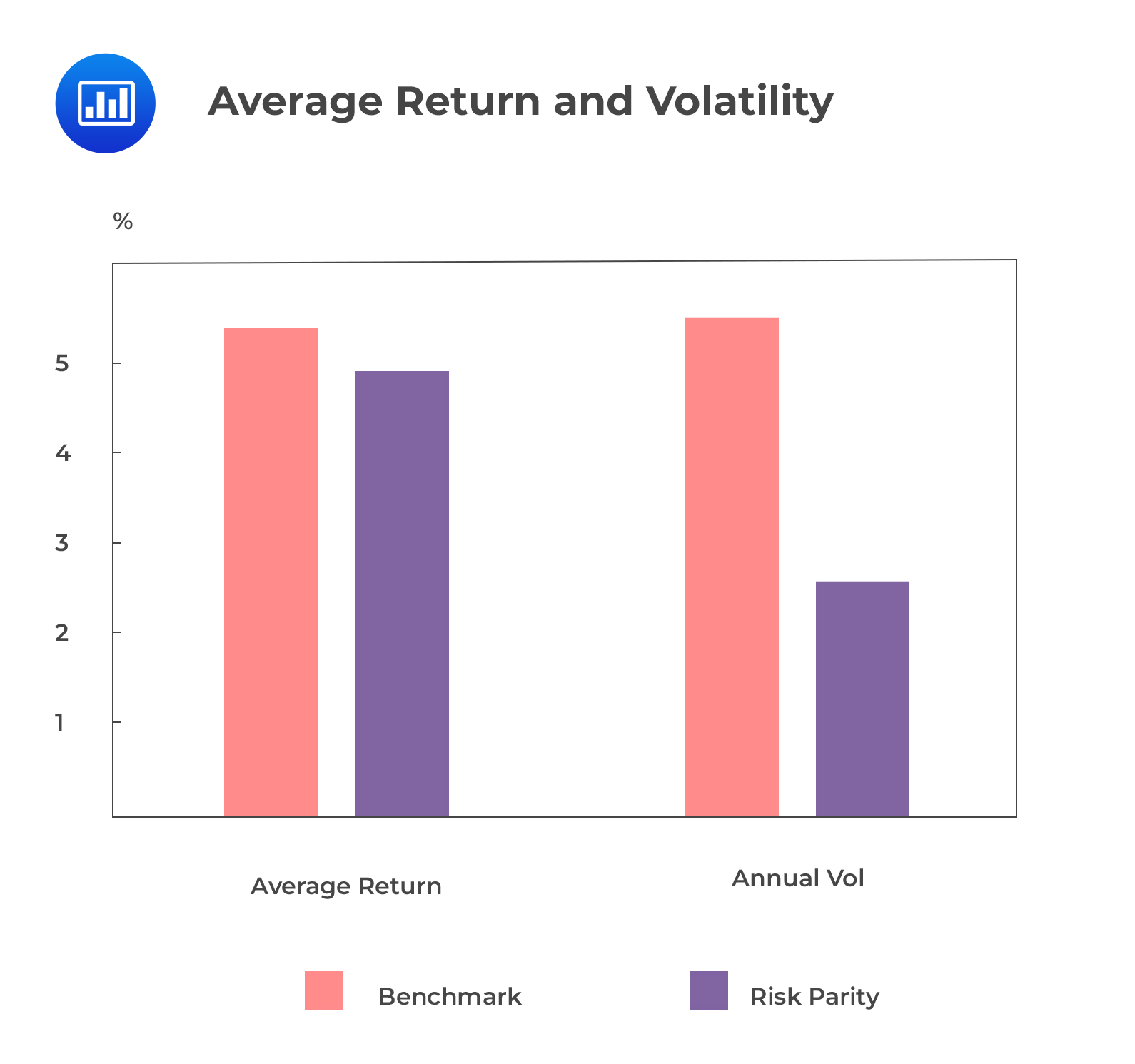 This will lead to the RP portfolio’s Sharpe ratio being twice more than that of the BM portfolio.
This will lead to the RP portfolio’s Sharpe ratio being twice more than that of the BM portfolio.
 According to the following table, we can see that the BM portfolio and six out of eight factors are negatively skewed. The kurtosis of all factors exceeds 3.0. BM and RP show low standard deviation and moderate mean returns compared to the eight-factor portfolio. This goes to show the diversification benefit.
According to the following table, we can see that the BM portfolio and six out of eight factors are negatively skewed. The kurtosis of all factors exceeds 3.0. BM and RP show low standard deviation and moderate mean returns compared to the eight-factor portfolio. This goes to show the diversification benefit.
$$\small{\begin{array}{l|c|c|c|c|c|c|c|c|c|c} {}& {\textbf{Earnings} \\ \textbf{Yield}} & {\textbf{Book-to-}\\ \textbf{Market}} &{\textbf{Earnings}\\ \textbf{Growth}} & \textbf{Momentum} & {\textbf{Earnings}\\ \textbf{Revision}} & \textbf{ROE} & \textbf{Debt/Equity}& {\textbf{Earnings}\\ \textbf{Quality}} & \textbf{BM} & \textbf{RP} \\ \hline \textbf{Mean} & 0.7\% & 0.4\% & 0.2\% & 0.6\% & 0.7\% & 0.5\% & 0.1\% & 0.4\% & 0.5\% & 0.4\% \\ \hline \textbf{Median} & 0.6\% & 0.1\% & 0.4\% & 0.8\% & 0.8\% & 0.6\% & 0.1\% & 0.4\% & 0.5\% & 0.4\% \\ \hline \textbf{Max} & 15\% & 29\% & 6\% & 11.7\% & 9\& & 11\% & 12\% & 5.3\% & 4.3\% & 4\% \\ \hline \textbf{Min} & -24\% & -12\% & -16\% & -32.7\% & -19\% & -27\% & -17\% & -3\% & -11\% & -3\% \\ \hline \textbf{Std.Dev} & 3.6\% & 4\% & 2\% & 5\% & 2\% & 4\% & 2.5\% & 1.2\% & 2\% & 0.7\% \\ \hline \textbf{Skewness} & -1 & 3 & -2.5 & -2.36 & -2.4 & -2 & -0.6 & 0.41 & -2.4 & 0.5 \\ \hline \textbf{Kurtosis} & 11.02 & 24 & 18 & 17 & 21 & 15 & 11.5 & 4 & 5.4 & 5.4\\ \end{array}}$$
Question
Which of the following is not a metric or visual used to assess a factor-based investment strategy’s backtesting?
- Maximum drawdown
- Distribution plots of factor returns
- Word cloud describing characteristics of the factor
Solution
The correct answer is C.
This is not a visual used for assessing the backtesting of a factor-based investment strategy.
A and B are incorrect. These are metrics and visuals used to assess backtesting.
Reading 42: Metrics and Visuals Interpretation
LOS 42 (c) Interpret metrics and visuals reported in a backtest of an investment strategy.
Get Ahead on Your Study Prep This Cyber Monday! Save 35% on all CFA® and FRM® Unlimited Packages. Use code CYBERMONDAY at checkout. Offer ends Dec 1st.