Value at Risk (VaR)

Value at Risk (VaR) measures the probability of underperformance by providing a statistical measure of downside risk.

In the case of a continuous random variable, VaR can be computed as follows:

$$ VaR\left(X\right)=-t \text{ where } P\left(X < t\right)=p $$

VaR represents the maximum possible loss on a portfolio over a given period in the future, with a given degree of confidence. The degree of confidence is typically expressed as \(1-p\).

For instance, if an asset has a one-day 5% VaR of $7,500, then there is a 5% probability that the asset will fall in value by at least $7,500 over one day under normal market conditions. This can also be given in terms of a confidence level, that is, we are 95% (100% − 5%) confident that the asset will experience a loss of at most $7,500 in one day.

The following is an illustration of the 5% VaR of a hypothetical portfolio:

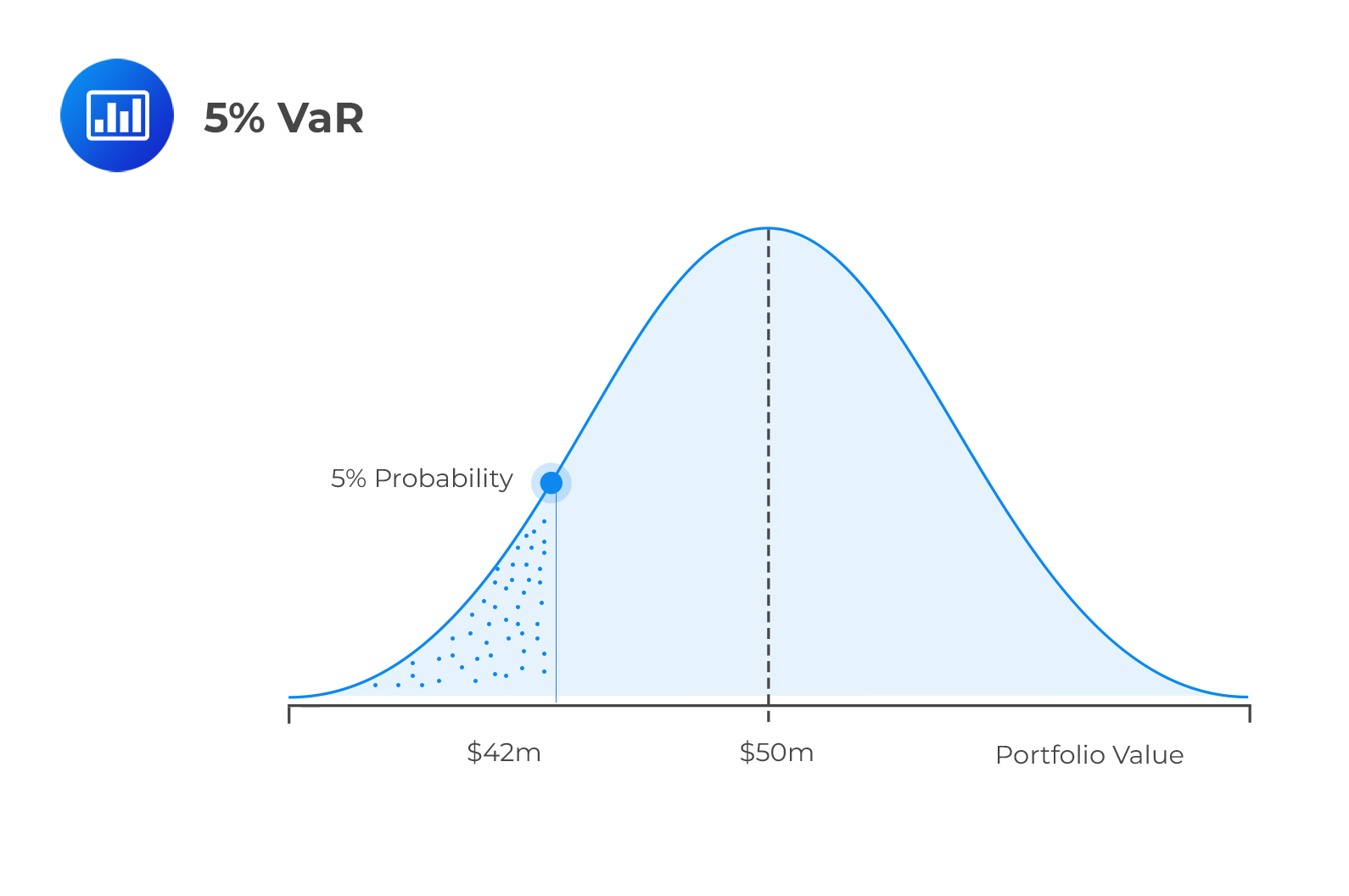The above illustration shows that the portfolio’s expected return is $50m. Additionally, the probability of realizing a return of less than $42m is 5%.

Question

A hypothetical portfolio B has an annual 1% VaR of $45,000. Which of the following statements is most likely true about the portfolio?

1. The expected minimum loss over one year, 1% of the time, is $45,000.
2. There is a 99% probability that the expected loss over the next year is more than $45,000.
3. The likelihood of losing $45,000 over the next year is 1%.

Solution

The correct answer is A.

An annual 1% VaR of $45,000 means that there is a 1% probability of a loss greater than $45,000.

B is incorrect. An annual 1% VaR of $45,000 means that there is a 99% probability that the portfolio will experience a loss of not more than $45,000 in one year.

C is incorrect. VaR does not specify the probability of losing a particular amount.

Reading 41: Measuring and Managing Market Risk

LOS 41 (a) Explain the use of value at risk (VaR) in measuring portfolio risk.