Linear or Log-Linear Model

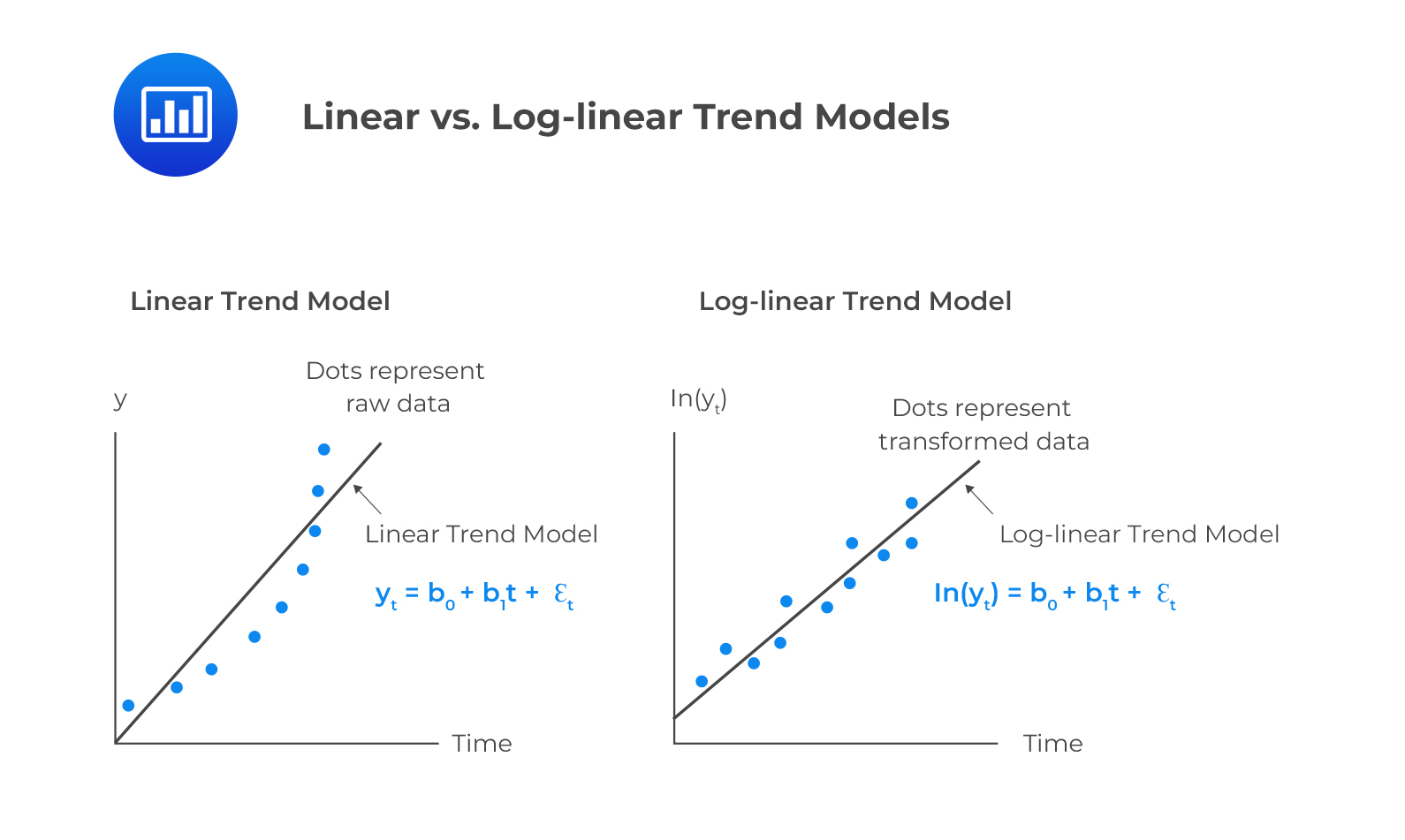
A linear trend model should model a time series that increases over time by a constant amount. On the other hand, a time series that grows at a constant rate should be modeled by a log-linear model.

To decide between linear and log-linear trend models, one should plot the data. If the data points are equally distributed above and below the regression line, use a linear trend model.

On the other hand, if the data points are persistently above or below the trend line, the residuals are serially correlated. This is a violation of one of the key regression model assumptions that residuals are uncorrelated across all observations. For instance, stock prices and sales data are best modeled using log-linear models.

Limitations of Trend Models

The error terms may be correlated. This violates the linear regression assumption that residuals are uncorrelated with each other, referred to as serial correlation.

Serial correlation makes the linear regression estimates inconsistent and invalid. Serial correlation can be detected by performing a Durbin-Watson test. If the Durbin-Watson statistic is significantly different from 2, then the residual terms are serially correlated.

We can correct serial correlation by transforming the data or using other regression models such as an autoregressive model, which will be discussed later in this reading.

Question

Neeth Shinu, a portfolio manager, has determined that the price of a certain stock has increased over the last decade, but its growth rate has remained relatively constant. The model that is most appropriate for predicting the future prices of the stock is:

1. \(\text{P}_{\text{t}}+\text{b}_{0}+\text{b}_{1}(\text{t})+\epsilon_{\text{t}}\)
2. \(\text{ln}(\text{p}_{\text{t}})=\text{b}_{0}+\text{b}_{1}(\text{p}_{\text{t}-1})+\epsilon_{\text{t}}\)
3. \(\text{ln}(\text{p}_{\text{t}})=\text{b}_{0}+\text{b}_{1}(\text{t})+\epsilon_{\text{t}}\)

Solution

The correct answer is C.

A log-linear model is most suitable for a time series that grows at a constant growth rate.

A is incorrect. It is a linear trend model which is suitable for a time series that increases over time by a constant amount.

 B is incorrect. This is an autoregressive model, which is appropriate in the presence of serial correlation.

Reading 5: Time Series Analysis

LOS 5 (b) Describe factors that determine whether a linear or a log-linear trend should be used with a particular time series and evaluate limitations of trend models.