Supervised Machine Learning, Unsupervi ...
Machine learning employs the idea that systems can learn from data, identify patterns,... Read More
Capital deepening is a condition in which an economy’s capital per worker (capital-labor ratio) is rising. The rate of change in the capital stock per labor hour. measures capital deepening. On the other hand, technological progress is the innovation of new and advanced technology that improves production methods.
Before discussing the impact of capital deepening and technological progress, we need to build a foundation by discussing the production function.
Some of the factors that lead to economic growth are physical and human capital, improved technology, and other inputs such as natural resources. A Production function is a quantitative model that relates factors of production, technology, and aggregate output.
For instance, a two-factor production function is represented as:
$$ Y=AF(K,L) $$
Where:
\(Y\) = Aggregate output in the economy.
\(L\) = Quantity of labor.
\(K\) = Capital.
\(A\) = Total factor production (TFP).
Note that TFP represents the general level of production or technology in the economy.
The Cobb-Douglas production function provides a basis for concrete results since it is easy to analyze and accommodates historical data of inputs and outputs. It is given by:
$$ Y=F\left(K,L\right)=K^\alpha L^{1-\alpha} $$
Where:
\(K\) = Capital.
\(L\) = Labor.
\(\alpha\) = Share of GDP paid out to suppliers of capital.
The variable \(\alpha\) is assumed to take values 0 and 1. This is true because, in microeconomics, profit is maximized when:
Considering the MP of capital (i), the Cobb-Douglas production becomes:
$$ MPK=\alpha AK^{\alpha-1}L^{1-\alpha}=\frac{aY}{K} $$
Let the MPK be equal to the rental price (r) so that:
$$ \frac{aY}{K}=r $$
Making \(\alpha\) the subject, we get:
$$ \alpha=\frac{rK}{Y} $$
This implies that \(\alpha\) is the ratio of capital income \(rK\) to output (GDP) Y or the proportion (share of capital) of the GDP paid to the suppliers. If we do the same for the MP of labor, it will be seen that the percentage of GDP spent on labor is \(1- \alpha\)
The Cobb-Douglas production function possesses properties that assist in examining the relationship between the aggregate output and the factors of production.
That is, an increase in factors of production leads to the same increase in the aggregate output. Under this property, the production function
$$ Y=AF(K,L) $$
can be transformed by multiplying by \(\frac{1}{L}\) to get:
$$ \frac{Y}{L}=Af\left(\frac{K}{L},\frac{L}{L}\right)=Af\left(\frac{K}{L},1\right) $$
Define \(y=\frac{Y}{L}\) as the output per worker (labor productivity) and \(k=\frac{K}{L}\) As the capital-labor ratio, the expression above becomes:
$$ y=Af\left(k,1\right) $$
If we write the Cobb-Douglas production function in terms of output per worker terms, then
$$ y=\frac{Y}{L}=A\left(\frac{K}{L}\right)^\alpha\left(\frac{L}{L}\right)^{1-\alpha}=Ak^\alpha $$
The last equation implies that labor productivity depends on the capital-to-labor ratio, technology (TFP), and proportion of capital in GDP \((\alpha)\).
The Cobb-Douglas production displays diminishing marginal productivity relative to each input. This property depends on the value of \(\alpha\). When \(\alpha\) tends to zero, the diminishing marginal returns to capital are very substantial, and additional output caused by additional capital decreases rapidly as the capital rises. Conversely, as \(\alpha\) tends to 1, the subsequent capital increase leads to additional output almost equal to the previous one (the impact of Diminishing Marginal Productivity reduces).
The diminishing marginal productivity property of the Cobb-Douglas production function assesses the impact of capital deepening and technological progress on economic growth and labor productivity. To illustrate this, we will refer to the graph below.
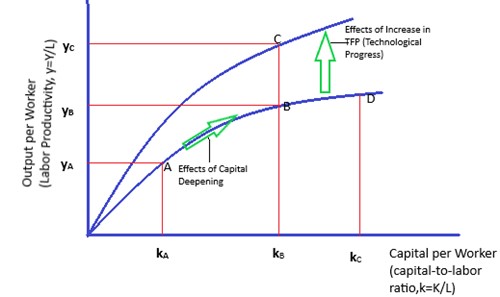
The capital deepening (represented by an increase in the capital-to-labor ratio) moves along the production curve, i.e., from points A to B in the graph above. When the capital-labor ratio rises to point B, the extra capital injection will have a minimum effect on per capita output (points B to D) because marginal product decreases.
The profit maximizes when the marginal cost (MC) equals the marginal product (MP). At this point, capital addition is stopped. This implies that capital deepening cannot be a factor for sustained economic growth when an economy reaches a stable state.
The technological progress (represented by TFP) results in corresponding upward movement (from point B to C) of the production function. Therefore, the economy can generate higher output per worker for a given size of capital per worker. Moreover, technological progress raises the marginal product of capital to its marginal cost, making the extra capital investments profitable and reducing the restriction diminishing marginal returns create.
Lastly, even in a stable economy, the per capita output will continue to grow with technological progress (rising TFP).
Question
Country Y has a high capital-to-labor ratio. Another country, Z, has a lower capital-to-labor ratio relative to country Y. There is a rising business investment in both countries. The impact on the growth rate of potential GDP is most likely to be:
- Felt more in country Y than in Z.
- Felt more in country Z than in Y.
- Same for both countries.
Solution
The correct answer is B.
Both countries will increase the capital-to-labor ratio due to rising business investments (capital deepening). However, country Z will experience more output per worker and an increased growth rate of the potential GDP since it runs at a lower capital per worker.
The growth rate for country Y is low because of the high level of capital per worker. Under this condition, extra capital is ineffective because of diminishing returns.
Reading 9: Economic Growth
LOS 9 (d) Contrast capital deepening investment and technological progress and explain how each affects economic growth and labor productivity.