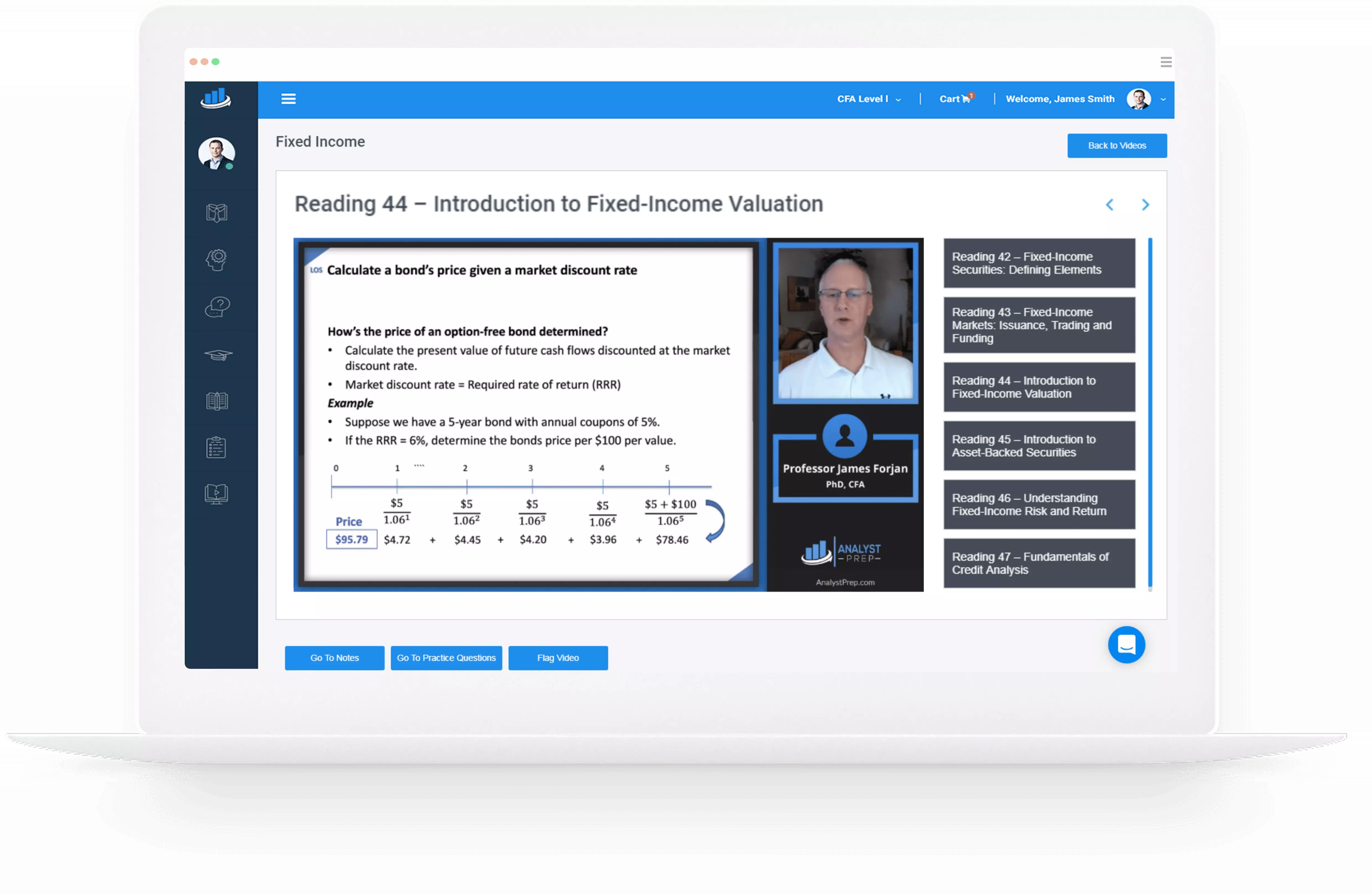
Determine the distribution of order statistics from a set of independent random variables
Order Statistics Order Statistics are distributions obtained when we look at test scores from a random sample arranged in ascending order, i.e., from the smallest to the largest. In recent years, the importance of order statistics has increased because of…
Calculate conditional probabilities
While it's crucial to grasp basic probability concepts, actuarial problems often require a deeper dive into complex scenarios where events are interdependent. This leads us to the concept of conditional probability. Conditional probability is the probability of an event occurring,…
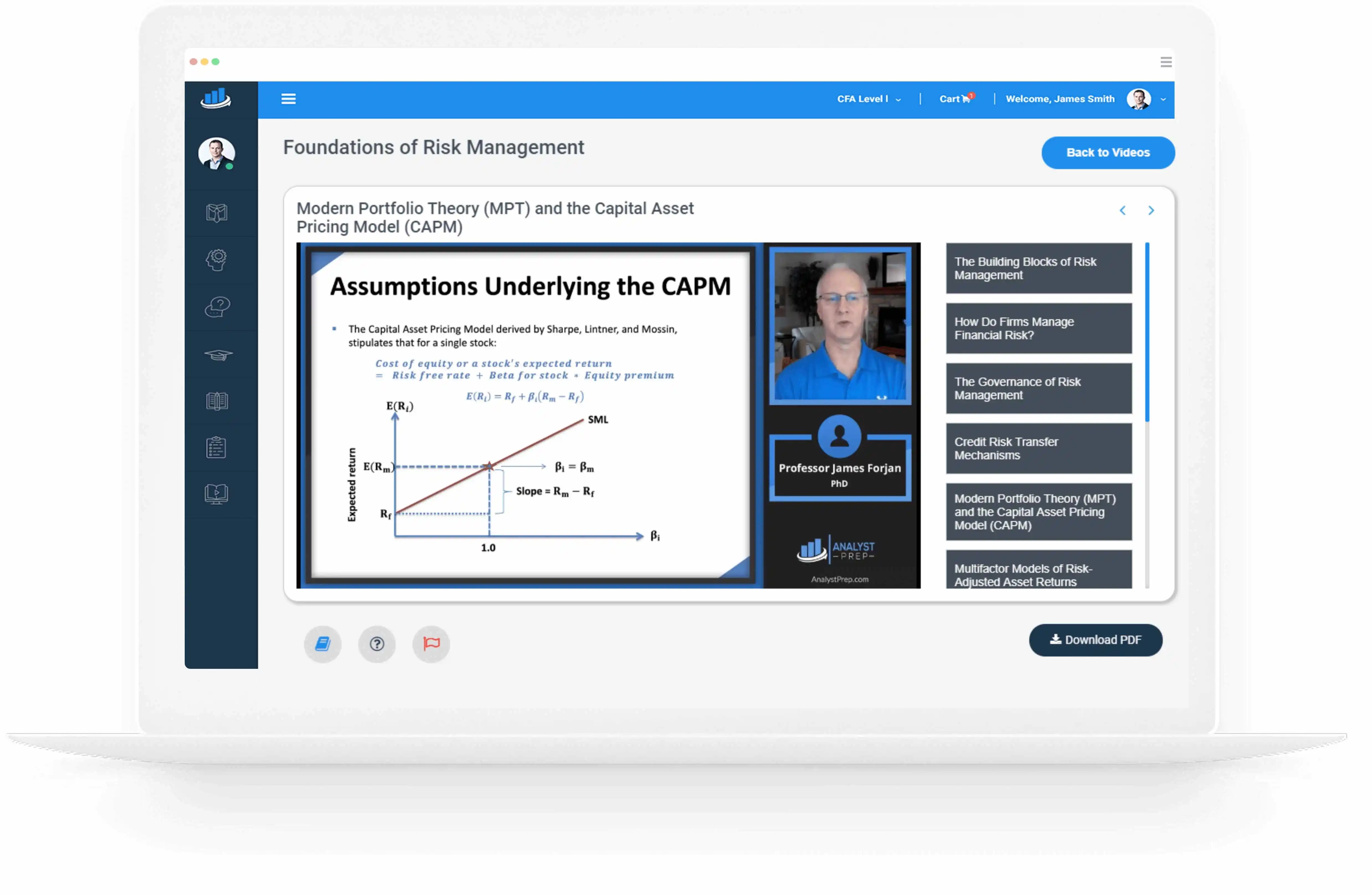
Apply the Central Limit Theorem to calculate probabilities for linear combinations of independent and identically distributed random variables
One of the most important results in probability theory is the central limit theorem. According to the theory, the sum of a large number of independent random variables has an approximately normal distribution. The theory provides a simple method of…
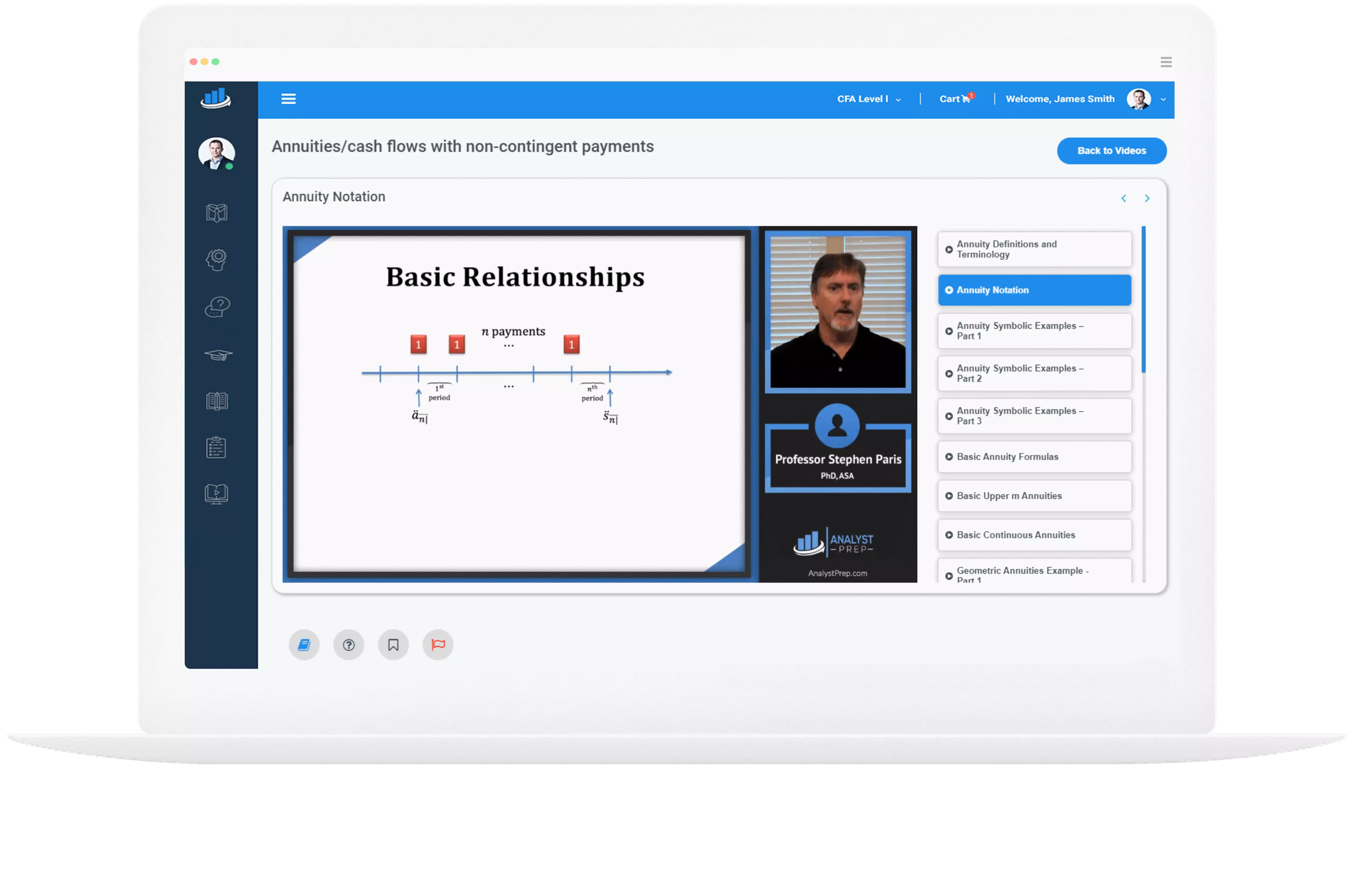
Calculate moments for linear combinations of independent random variables
In the previous reading, we defined \(Y=c_1X_1+c_2X_2+\ldots+c_pX_p\) to be a linear combination of the independent random variables \(X_1, X_2,\ldots, X_p\) where \(c_1,,\ c_2,\ldots,\ c_p\) are constants. We also proved that if \(X_1, X_2,\ldots,X_n\) are independent normal random variables with means…
Determine the distribution of order statistics from a set of independent random variables
Order Statistics Order Statistics are distributions obtained when we look at test scores from a random sample arranged in ascending order, i.e., from the smallest to the largest. In recent years, the importance of order statistics has increased because of…
Calculate variance and standard deviation for conditional and marginal probability distributions for discrete random variables only
Variance and Standard Deviation for Conditional Discrete Distributions Recall that, in the previous readings, we defined the conditional distribution function of \(X\), given that \(\text{Y}=\text{y}\) as: $$ \text{g}(\text{x} \mid \text{y})=\frac{\text{f}(\text{x}, \text{y})}{\text{f}_{\text{Y}}(\text{y})}, \quad \text { provided that } \text{f}_{\text{Y}}(\text{y})>0 $$ Similarly,…
Calculate moments for joint, conditional, and marginal discrete random variables
The \(n\)-th moment about the origin of a random variable is the expected value of its \(n\)-th power. In this reading, however, we will mostly look at moments about the mean, also called central moments. The \(n\)-th central moment of…
Determine conditional and marginal probability functions for discrete random variables only
Marginal Probability Distribution In the previous reading, we looked at joint discrete distribution functions. In this reading, we will determine conditional and marginal probability functions from joint discrete probability functions. Suppose that we know the joint probability distribution of two…
Explain and perform calculations concerning joint probability functions and cumulative distribution functions for discrete random variables only
Joint Discrete Probability Distributions We are often interested in experiments that involve the intersection of two or more events. For example: An experimenter tossing a fair die is interested in the intersection of getting, say, a 5 and a 6….
Calculate the expected value, variance, and standard deviation of both the loss random variable and the corresponding payment random variable upon the application of policy adjustments.
In the previous reading, we covered the fundamental ideas of deductibles, coinsurance, benefit limits, and inflation in the context of insurance. In this reading, we will focus on more quantitative aspects. Specifically, we will perform calculations to determine the expected…