Define and calculate conditional probabilities

Conditional Probability

Given two events \(A\) and \(B\), the conditional probability of event \(A\) occurring, given that event \(B\) has occurred, is the probability of event \(A\) and \(B\) occurring over the probability of event \(B\) occurring as shown by the formula below:

$$ P\left( A|B \right) =\frac { P\left( A\cap B \right) }{ P\left( B \right) } $$
as long as \(P (B) > 0\).

As shown in the diagram below, the probability of \(A\) given \(B\) occurred is the shaded region \(A \cap B\).

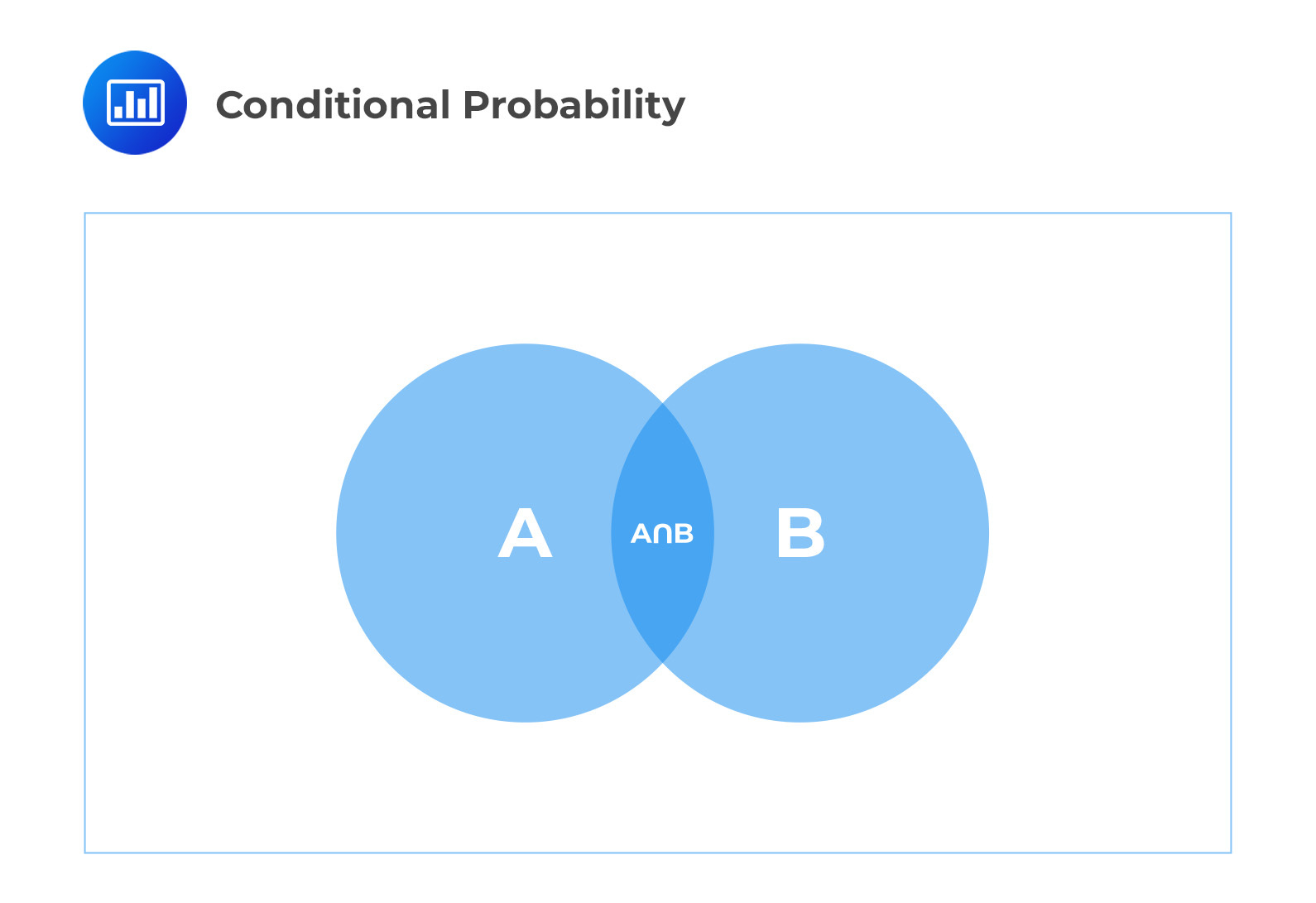Example: Conditional Probability

Suppose 50% of the students in a school take geometry, 30% take history, and 15% take both geometry and history. Given that a student selected at random takes geometry, what is the probability he or she also takes history?

Solution

Let event \(A\) be “takes geometry” and event \(B\) be “takes history.”

\(P \left(B \right) = 0.30\)

\(P \left(A \cap B \right) = 0.15\)

$$ P\left( B|A \right) =\frac { P\left( A\cap B \right) }{ P\left( A \right) } ={ 0.15 }/{ 0.50 }=0.30\quad or\quad 30\% $$

This concept can be extended to more than 2 events as shown in the formula for 3 events below:

$$ P\left( C|A\cap B \right) =\frac { P\left( A\cap B\cap C \right) }{ P\left( A \right) \times P\left( B|A \right) } $$

Example: Conditional Probability

Suppose that the students at a university are grouped such that:

 45% take chemistry

 35% take biology

 25% take math

 10% take chemistry and math

 5% take chemistry and biology

 3% take biology and math

 1% take all three subjects

Calculate the probability that a student takes math, given that they take chemistry and biology.

$$P\left( \text{Math|Chemistry and Biology} \right) =\frac{{ P\left( \text{Math and Chemistry and Biology} \right) }}{{ P\left( \text{Chemistry} \right) \times P\left( \text{Biology|Chemistry} \right) }}$$

$$\begin{align*} P\left( \text{Biology|Chemistry} \right) & =\frac{{ P\left( \text{Biology and Chemistry} \right) }}{{ P\left( \text{Chemistry} \right) }} \\ & ={ .05 }/{ .45 }={ 1 }/{ 9 } \\ \end{align*} $$

$$P(\text{Math|Chemistry and Biology})=\frac{{ .01 }}{{ \left( { .45\times .05 }/{ .45 } \right) }}={ .01 }/{ .05 }={ 1 }/{ 5 }=.20\quad or\quad 20\%$$

The definition of conditional probability can be rewritten to come up with multiplication rule for probabilities:

$$P(A\cap B)=P(A|B)\bullet P(B)$$

Also, if the events A and B are independent, then:

$$P(A|B)=P(A)$$

Learning Outcome

Topic 1.e: General Probability – Define and calculate conditional probabilities.