Uses of the t-test and the z-test

The z-test

The z-test is the ideal hypothesis test to conduct in a normal distribution of a random variable. In addition, the variance of the population must be known. The z-statistic refers to the test statistic computed for hypothesis testing.

Testing H₀: μ = μ₀ using the z-test

Given a random sample of size n from a normally distributed population with mean μ and variance σ^2_, and a sample mean X̄, we can compute the z-statistic as:

$$ \text z-\text{statistic} =\cfrac {(\bar{X} – \mu_0)}{\left(\frac {\sigma}{\sqrt n} \right)} $$

Where:

\(\bar{X}\) is the sample mean.

\(μ_0\) is the hypothesized mean of the population.

\(σ\) is the standard deviation of the population.

\(n\) is the sample size.

Once computed, the z-statistic is compared to the critical value that corresponds to the level of significance of the test. For example, if the significance level is 5%, the z-statistic is screened against the upper or lower 95% point of the normal distribution (±1.96). The decision rule is to reject the H₀ if the z-statistic falls within the critical or rejection region.

Example: z-test

Academics carried out a study on 50 former United States presidents and found an average IQ of 135. You are required to carry out a 5% statistical test to determine whether the average IQ of presidents is greater than 130. (IQs are distributed normally, and previous studies indicate that σ = 25.)

Solution

First, you have to state the hypothesis:

H₀: μ = 130

H₁: μ > 130

Assuming the H₀ is true, \(\frac {(\bar{X} – 130)}{\left(\frac {\sigma}{\sqrt n} \right)} \sim N(0,1)\).

The z-statistic is \(\cfrac {(135 – 130)}{\left(\frac {25}{\sqrt {50}} \right)} = 1.414\).

This is a right-tailed test. Therefore, we compare our test statistic to the upper 95% point of the standard normal distribution (1.6449). Since 1.414 is less than 1.6449, we do not have sufficient evidence to reject the H₀. As such, it would be reasonable to conclude that the average IQ of U.S. presidents is not more than 130.

The t-test

The t-test is based on the t-distribution. The test is appropriate for testing the value of a population mean when:

• σ is unknown; and
• The sample size is large (n ≥ 30), and if n < 30, the distribution must either be normal or approximately normal.

Testing H₀: μ = μ₀ Using the t-test

We compute a t-statistic with n – 1 degrees of freedom as:

$$ t_{n-1} = \cfrac {(\bar{X} – \mu_0)}{\left(\frac {s}{\sqrt n} \right)} $$

Where:

\(\bar{X}\) is the sample mean.

\(μ_0\) is the hypothesized mean of the population.

\(s\) is the standard deviation of the sample.

\(n\) is the sample size.

Example: t-test

The annual rate of rainfall (cm) in a certain equatorial country over the last 10 years is given below:

{ 25   26   25    27   28   29   28   27   26   25 }

Financial analysts in the country wish to determine whether the average rate of rainfall has increased from its former value of 23. Carry out a statistical test at the 5% level.

Solution

As always, you should begin by stating the hypothesis:

H₀: μ ≤ 23

H₁: μ > 23

If we assume that the annual rainfall quantities are distributed normally and recorded independently, then:

$$ \cfrac {(\bar{X} – 23)}{\left(\frac {S}{\sqrt n} \right)} \sim t_{n- 1} $$

Please, confirm that X̄ = 26.6 and S = 1.43.

Therefore, our t-statistic = \(\cfrac {(26.6 – 23)}{\left(\frac {1.43}{\sqrt {10}}\right)} = 7.96\).

Our test statistic (7.96) is greater than the upper 95% point of the t_0.05,9 distribution (1.833).

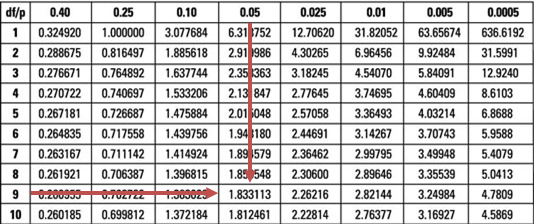
Therefore, we have sufficient evidence to reject the H₀. As such, it is reasonable to conclude that the average annual rainfall has increased from its former long-term average of 23.

Question

What is the value of t in the example above if the level of significance is reduced from 5% to 0.5%, and does this change the decision rule?

1. 2.02; it does not change the decision rule.
2. 3.25; it does not change the decision rule.
3. 3.25; it does change the decision rule.

Solution

The correct answer is B.

A quick glance at the t_0.005,9 distribution when α = 0.5% gives a value of 3.25.

However, the evidence against the H₀ is too strong since our test statistic (7.96) is still greater than 3.25. As such, the conclusion would remain unchanged.

(Note to candidates: You might also work out the solutions to the above examples and questions using p-values instead of critical values. The decision rules would remain unchanged provided you work out the p-values correctly.)