Introduction to Probability Distributions, Probability Functions, and Types of Variables

Probability Distribution

The probability distribution of a random variable “X” is basically a graphical presentation of the probabilities of all possible outcomes of X. A random variable is any quantity for which more than one value is possible. An example of a random variable is the price of quoted stocks. Simply put, a probability distribution gathers all the outcomes and goes a step further to indicate the probability associated with each outcome.

Example: Probability Distribution

What if we rolled a six-sided dice? The set of possible outcomes is:

{1   2   3   4   5   6}

Each of these outcomes would occur with a probability of 1/6 because each of them has an equal chance of occurring. Consequently, the probability distribution would be a straight line:

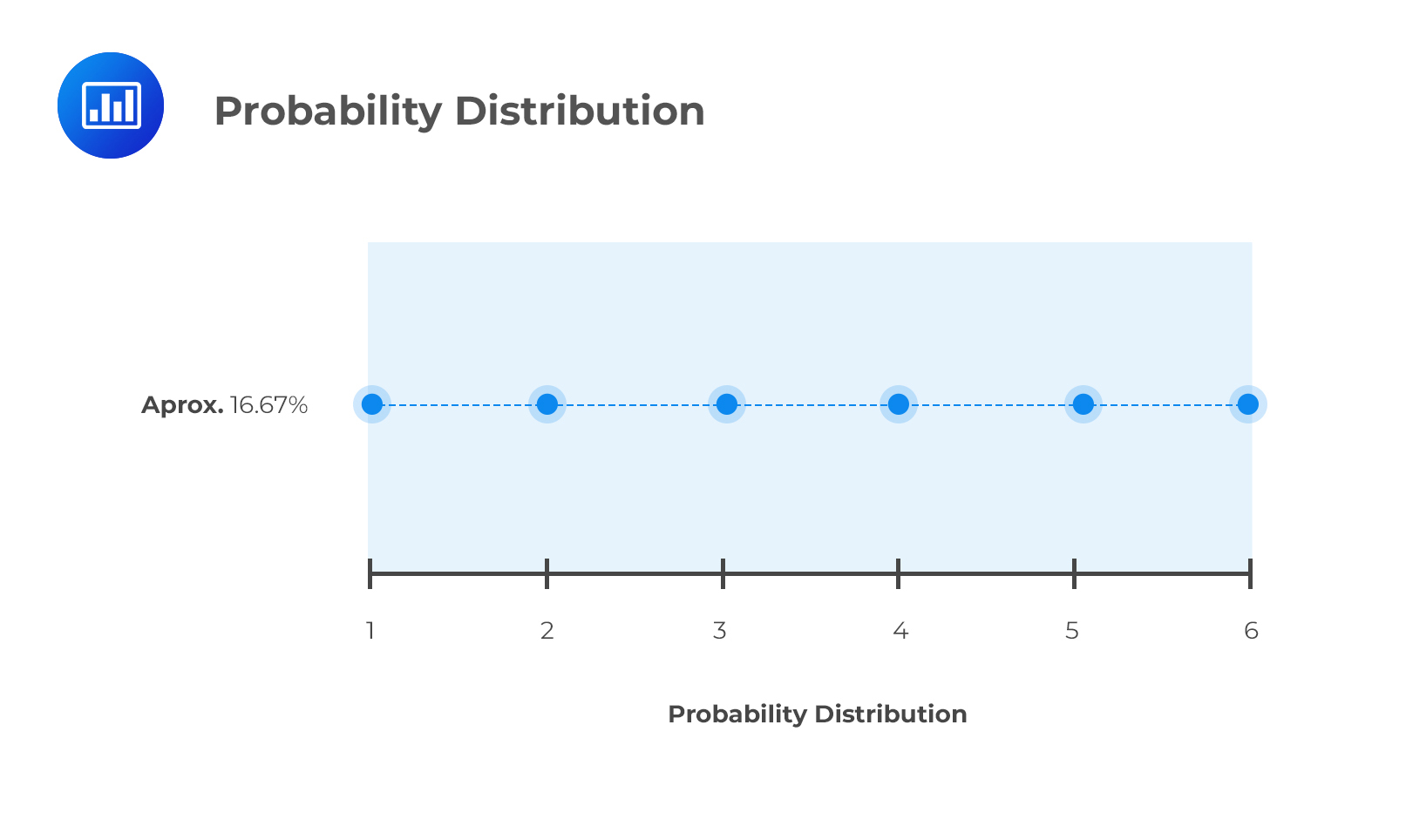
Note to candidates: although the above distribution is a straight line, most real life distributions are usually curved. The CFA curriculum particularly delves into the bell-shaped normal distribution.

Discrete Random Variables

A discrete random variable can take on a finite number of outcomes.

Examples

1. If we roll a dice, there are 6 possible outcomes. Therefore, the outcomes are discrete and random.
2. The number of CFA finalists employed within a given year is a discrete random variable.

Continuous Random Variables

A continuous random variable is that which has an infinite number of possible outcomes. A good example can be the rate of return on a stock. For instance, the return can be 6% or between 6% and 7%, in which case it can take on 6.4%, 6.41%, 6.412%, or even 6.412325%, i.e., infinite values.

Probability Function

A probability function gives the probability of a random variable X taking on a value “x.” The probability functions of discrete and continuous random variables are slightly different.

For a discrete random variable, the probability function, P(x), satisfies the properties below.

1. P(X = x) = P(x)
   In statistics, P(x) is said to be a probability mass function
2. P(x) is always nonnegative for all x
3. The sum of the probabilities of all possible outcomes = 1.

For a continuous random variable, the probability function, f(x), satisfies the properties listed below.

1. The probability that x is between two values, a and b is
   $$ P\left\{ a\le x\le b \right\} =\int _{ a }^{ b }{ f\left( x \right) dx } $$
   f(x) is said to be a probability density function(pdf)
2. f(x) is nonnegative for all x
3. The integral of the probability function is 1, that is,
   $$ \int _{ -\infty }^{ \infty }{ f\left( x \right) dx=1 } $$

Reading 9 LOS 9a:

Define a probability distribution and distinguish between discrete and continuous random variables and their probability functions.