Cumulative Distribution Function (CDF)

A cumulative distribution function, F(x), gives the probability that the random variable X is less than or equal to x:

$$ P(X ≤ x) $$

By analogy, this concept is very similar to the cumulative relative frequency.

A cumulative distribution is the sum of the probabilities of all values qualifying as “less than or equal to” the specified value. Perhaps an example will make this concept clearer.

Example: Cumulative Distribution

Imagine flipping a coin three times. You would end up with the following probability distribution of the number of heads obtained:

$$ \begin{array}{c|c|c|c} \text{Heads (outcomes)} & {0} & {1} & {2} & {3} \\ \hline \text{Probability} & {1/8} & {3/8} & {3/8} & {1/8} \\ \end{array} $$

To come up with a cumulative distribution function, we have to calculate the cumulative probabilities.

The cumulative probability that X is less than or equal to zero is 1/8.

To find the cumulative probability that X is less than or equal to 1, we add P(X = 0) and (P = 1):

$$ P(X \le 1) =\cfrac {1}{8} + \cfrac {3}{8} = \cfrac {1}{2} $$

Similarly,

$$ P(X \le 2) = \cfrac {1}{8} + \cfrac {3}{8} + \cfrac {3}{8} = \cfrac {7}{8} $$

Lastly,

$$ P(X \le 3) = \cfrac {1}{8} + \cfrac {3}{8} + \cfrac {3}{8} +\cfrac {1}{8} = 1 $$

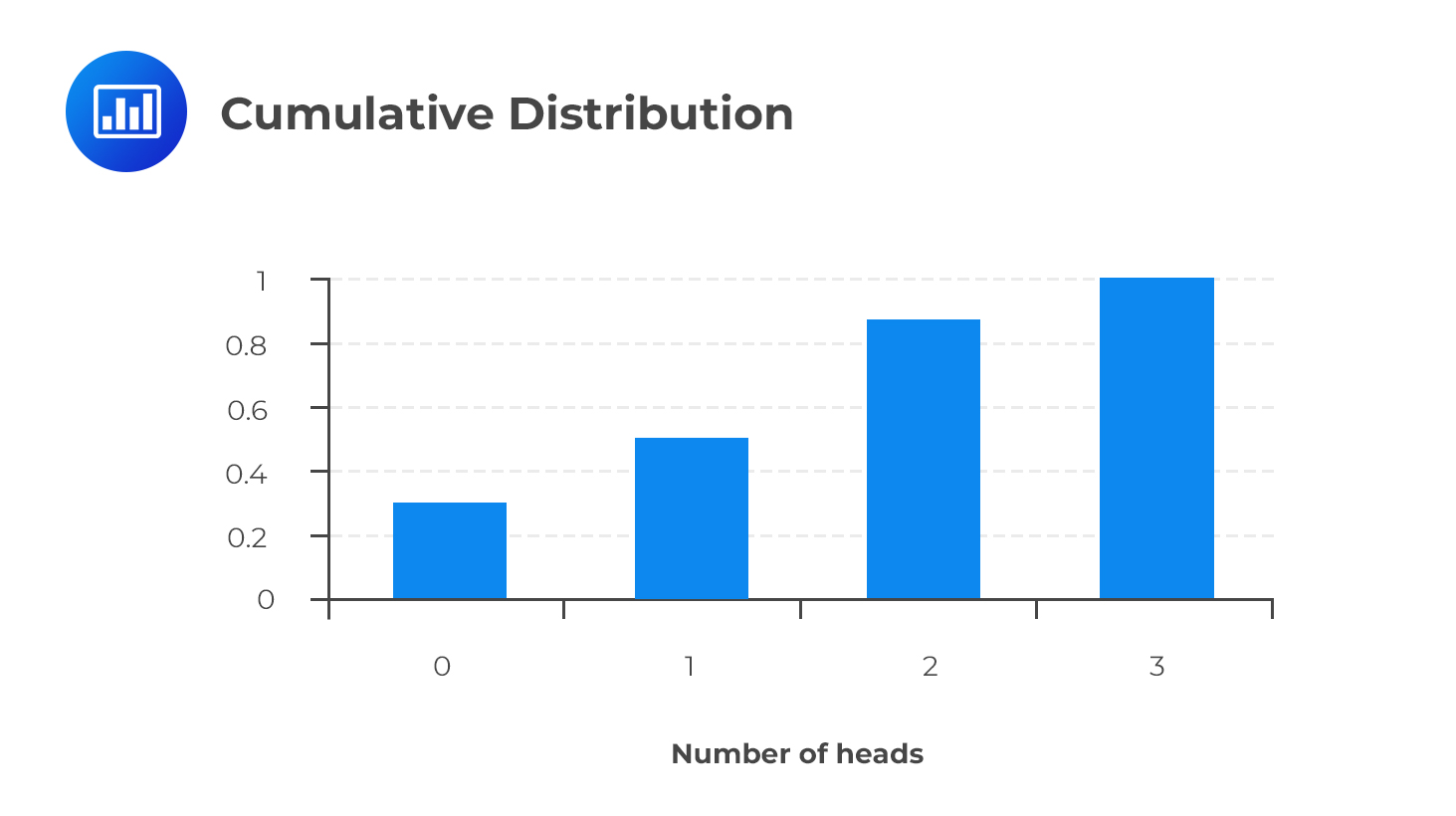
$$ \begin{array}{c|c|c|c} \text{Heads (outcomes)} & {0} & {1} & {2} & {3} \\ \hline \text{Probability} & {1/8} & {3/8} & {3/8} & {1/8} \\ \hline \text{Cumulative prob.} & {1/8} & {4/8} & {7/8} & {8/8} \\ \end{array} $$

The CDF has two main properties:

1. all values in the CDF are between 0 and 1; and
2. the CDF either increases or remains constant as the value of the specified outcome increases.

Interpreting the Cumulative Distribution Function

A cumulative distribution function can help us to come up with cumulative probabilities pretty easily. For example, we can use it to determine the probability of getting at least two heads, at most two heads, or even more than two heads. For example, the probability of at most two heads from the cumulative distribution above is 0.875.

Question

Variable X can take the values 1, 2, 3, and 4. The probability of each outcome has been given below.

$$ \begin{array}{c|c|c|c|c} \text{Outcome} & {1} & {2} & {3} & {4} \\ \hline \text{Probability} & {0.2} & {0.3} & {0.35} & {0.15} \\ \end{array} $$

Construct a table showing the cumulative distribution and use it to determine P(X ≤ 2).

A. 0.5

B. 0.3

C. 0.85

Solution

The correct answer is A.

You simply sum up the probabilities up to and including a given outcome and come up with a table similar to the one below:

$$ \begin{array}{c|c|c|c|c} \text{Heads (outcomes)} & {1} & {2} & {3} & {4} \\ \hline \text{Probability} & {0.2} & {0.3} & {0.35} & {0.15} \\ \hline \text{Cumulative prob.} & {0.2} & {0.5} & {0.85} & {1} \\ \end{array} $$

From the table, it is clear that \(P(X \le 2) = 0.5\).