Value and Price of Futures Contracts

Recall that during the initiation of a forward commitment, no cash changes hands. Further, the forward commitment is neither a liability nor an asset to a buyer or the seller. As such, the value of both the forward contract and futures contract is zero: $$V_0(T)=0$$ Consider an underlying with no associated costs or benefits. Like forward contracts, the futures price is calculated by compounding the spot price of the underlying using the risk-free rate: $$f_T(0)=S_0(1+r)^T$$ Where: \(f_T(0)=\) Futures forward price. \(S_0=\) Spot price of the underlying at time \(t=0\). \(r=\) Risk-free rate. \(T=\) Time to maturity. Note that, like forward contracts, we have used discrete compounding. However, continuous compounding is also preferred in futures contracts if the underlying assets comprise a portfolio, such as commodities, fixed income, and equity. Also, continuous compounding is preferred when the underlying is foreign exchange denominated in two currencies. Using continuous compounding, the future price is given by: $$f_T(0)=S_0e^{rT}$$

Cost of Carry and Futures Price

Like forward contracts, the price of futures whose underlying has income (I) and costs (C) is adjusted as follows: $$f_T(0)=[S_0-PV_0(I)+PV_0(C)](1+r)^{T}$$ Where: \(PV_0(I)=\) Present value of income or benefit associated with the underlying at time \(t=0\). \(PV_0(C)=\) Present value of costs associated with the underlying at time \(t=0\)

Example: Futures Price Valuation

Minners Inc. enters a futures contract on an exchange via a financial intermediary to buy 80 kilos of gold. The current spot price is $52,950 per kilo. If the risk-free rate of return is 3%, what is the no-arbitrage futures price for settlement in 95 days?

Solution

The futures price is equal to the compounded value of the spot price of the underlying at the risk-free rate for a period \(T\): $$\begin{align*}f_T(T)&=S_0(1+r)^T\\&=\$52,950(1.03)^{\frac{95}{365}}\\&=\$53,358.94\end{align*}$$

Mark-to-Market Valuation of a Future Contract Compared to a Forward Contract

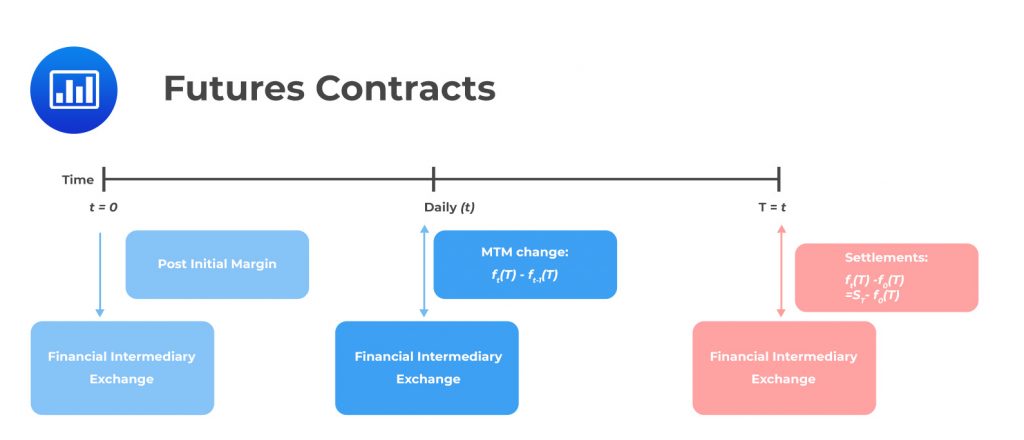
As time passes, the value of futures and forward contracts changes. However, the forward contract price remains constant until maturity. As seen previously, for the long position, the value of a forward contract during its life is calculated as the difference between the current spot price and the present value of the original forward price: $$V_t(T)=S_t-F_0(T)(1+r)^{-(T-t)}$$ The MTM value of the forward contract is not settled until its expiration date, which causes counterparty risk. On the other hand, the futures price changes depending on market conditions. Moreover, the daily settlement resets the MTM value to zero. Besides, the variation margin is exchanged to cover the difference, decreasing counterparty risk. Note that the cumulative MTM gain or loss is approximately equal to that of a comparable forward contract.

Interest Rate Futures and Forward Contracts

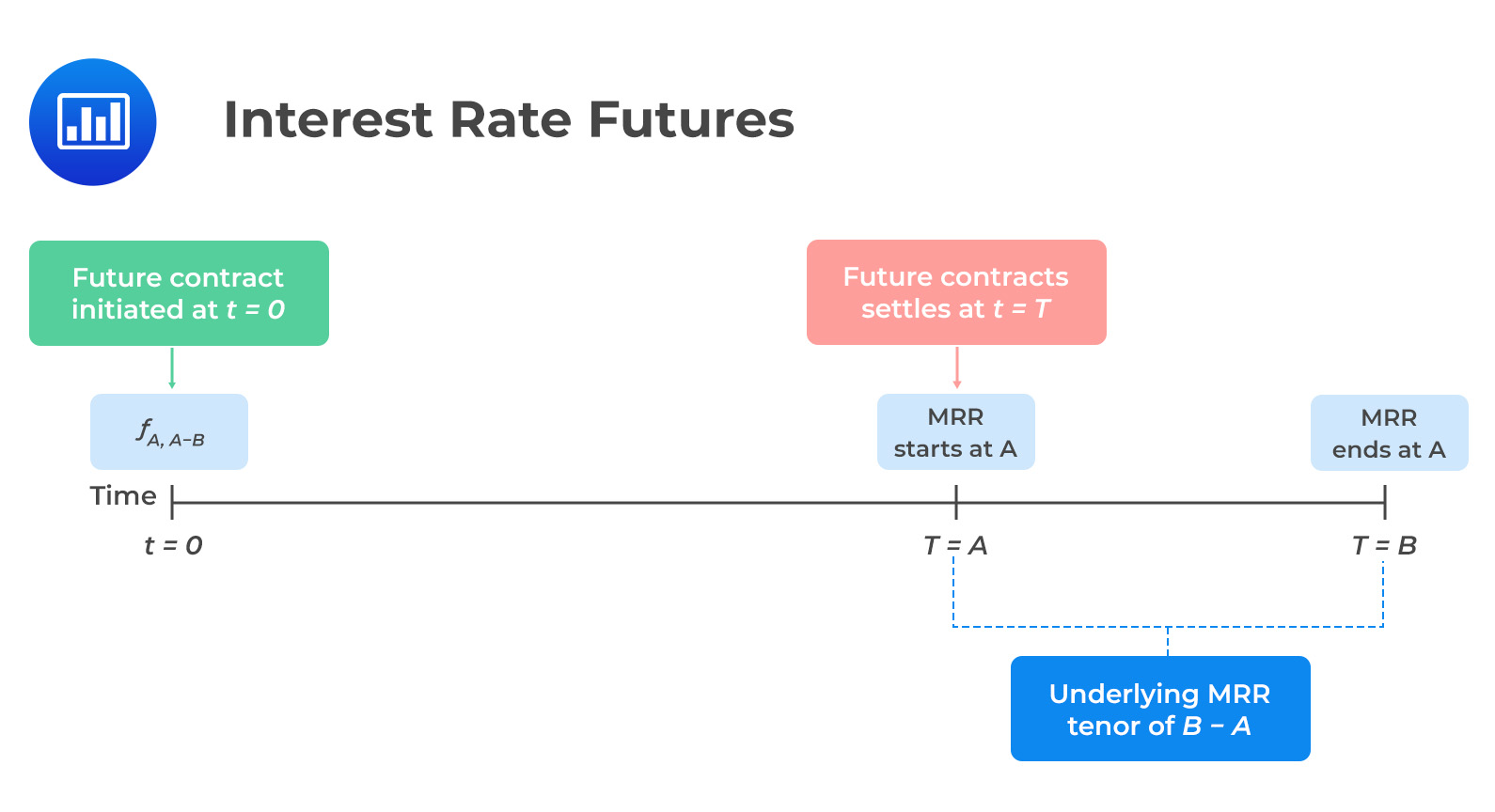
Remember that a forward rate agreement (FRA) uses implied forward rates as a no-arbitrage fixed rate. In this instance, the counterparties exchange fixed for floating payments at a specified time in the future. The futures contracts on short-term interest rates are more liquid and standardized than FRAs. These contracts are often available for monthly and quarterly market reference rates (MRRs).

Description of Interest Rate Futures

As is the case in FRA, the underlying of the interest rate futures is the market reference rate on a hypothetical amount of money at a future date. However, interest rate futures trade on a price basis, given by the following formula: $$f_{A,B-A}=100-(100\times\text{MRR}_{A,B-A})$$ Where: \(f_{A,B-A}=\) futures price for the market reference rate for \(B – A\) periods that begin in A period \((MRR_{A, B-A})\). Note that the formula \(f_{A, B-A}=100-(100\times\text{MRR}_{A, B-A})\) can be written as \(f_{A, B-A}=100-\text{yield}\). Intuitively, the (100 – Yield) price convention leads to an inverse price versus yield relationship that differs from the price of a zero-coupon bond at a contract rate. As such, a long futures position receives MRR in A period while the short position pays MRR in A period. In summary, the long position (lender) gains as prices rise and future MRR falls. In contrast, the short position (borrower) gains as prices fall and future MRR rises.

Interest Rate Futures Settlement

The daily settlement of the interest futures occurs depending on the price changes, regarded as futures contract basis point value (BPV) and calculated as follows: $$\text{Futures contract BPV}=\text{Notional principlal}\times0.01\%\times\text{Period}$$ For instance, consider USD 50 million for a 3-month MRR of 3% for 180/360 days. The futures contract BPV is: $$\text{Futures contract BPV}=50,000,000\times0.01\%\times\bigg(\frac{180}{360}\bigg)=\$2,500$$

Example: Calculating Futures Contracts Gains or Losses

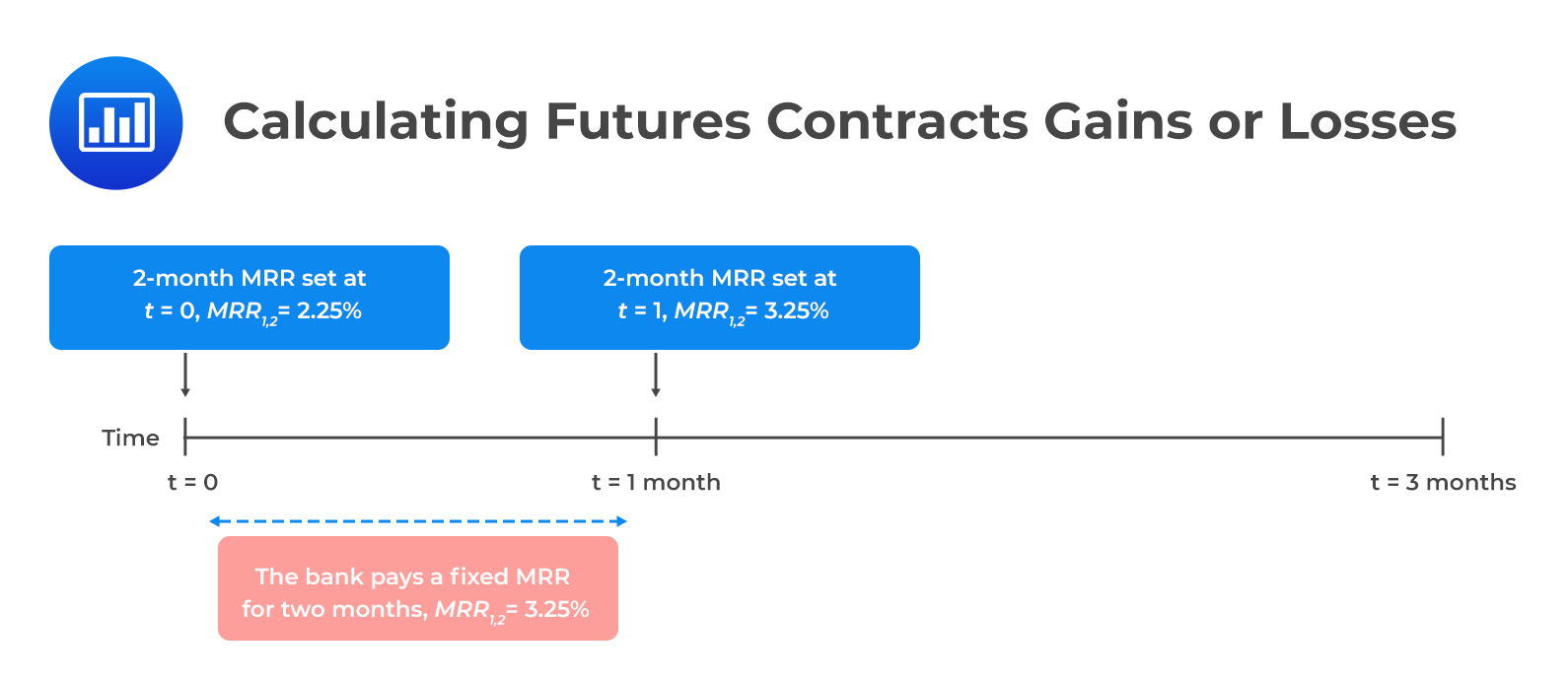
A&M Bank has issued its clients a USD 10 million three-month loan at a fixed rate. To finance the loan, the bank has borrowed a one-month variable MRR. To hedge against interest rate risk, the bank sells futures contracts on two-month MRR. Assume that the bank agrees to sell the futures at $97.75, but the actual settlement price is $96.75. The cumulative gain/loss to the contract from the bank’s perspective is closest to:

Solution

We need to start by calculating the contract’s BPV: $$\begin{align*}\text{Futures contract BPV}&=\text{Notional principal}\times0.01\%\times\text{Period}\\&=10,000,000\times0.01\%\times\frac{2}{12}\\&=\$166.67\end{align*}$$ We need to calculate corresponding market reference rates (MRRs) for both prices.  Note that $$f_{A, B-A}=100-(100\times\text{MRR}_{A, B-A}) $$ Therefore; $$ \begin{align*}96.75&=100-(100\times\text{MRR}_{A, B-A})\rightarrow MRR_{1,2}=3.25\%\\ 97.75&= 100-(100\times\text{MRR}_{A, B-A})\rightarrow\text{MRR}_{1,2}=2.25\%\end{align*} $$ The bank has made a 100bps gain \((=3.25\%-2.25\%)\). In monetary terms, the bank has made a cumulative gain of \(\$16,667 (= \text{Futures contract BPV} \times \text{100bps})\) on the contract.

Question

Which of the following best describes the difference between the price of a futures contract and its value? A. The price determines the profit to the buyer, and the value determines the profit to the seller. B. The futures price is fixed at the start, and the value starts at zero and changes throughout the contract’s life. C. The futures contract value is a benchmark against which the price is compared to determine whether a trade is advisable.

Solution

The correct answer is B. The futures price is fixed at the start, whereas the value starts at zero and then changes, either positively or negatively, throughout the contract’s life.