Why Forward and Futures Prices Differ
Forward and futures contracts share similar features; however, how they are traded and... Read More
Options are derivative instruments that give the option buyer the right, but not the obligation, to buy (call option) or sell (put option) an asset from (or to) the option seller at a fixed price on or before expiration.
In other words, options are contingent claims that give the option buyer the right but not the obligation to transact the underlying, and the option seller is obligated to meet the obligation chosen by the buyer. The payoff of an option is either positive or zero. The profit, on the other hand, can be negative because of the option premium.
An option’s time value and exercise value constitute the value of an option. The exercise value of an option would be the value if it were immediately exercisable. On the other hand, an option’s time value reflects the passage of time and variability of the underlying.
The moneyness of an option describes the relationship between the underlying price and the exercise price.
Now we look into these factors, considering the European options with no associated costs or benefits of owning an underlying asset.
Remember that in call options, the buyer has the right but not the obligation to buy the underlying. Moreover, the call option will only be exercised if the payoff is positive. Otherwise, the option expires worthless, and the option buyer incurs a loss equal to the option premium paid to the seller.
That is, the buyer would only exercise (buy the underlying) the option if (S_T>X). As such, the payoff (exercise value) to the buyer at expiration is given by:
$$c_T=\text{max}(0, S_T-X)$$
Conversely, the exercise to the seller at expiration is:
$$-c_T=-(\text{max}(0, S_T-X))$$
In other words, the exercise value of a call option is greater than either zero or the underlying price at expiration minus the exercise price.
On the other hand, in a put option, the buyer has the right but not an obligation to exercise the option at expiry. Exercising the option means that the buyer sells the underlying \(S_T\) at the exercise price \(X\) at expiration. As such, the put option is only exercisable if \(S_T<X\).
Therefore, the payoff to the buyer is given by:
$$p_T=\text{max}(0, X-S_T)$$
Conversely, the payoff to the put option seller is
$$-p_T=-(\text{max}(0, X-S_T))$$
At any time before maturity \((t<T)\), the investors estimate the value of options based on the underlying spot price \(S_t\) and the exercise price, \(X\).
The exercise value of a call option is the value of an option contract at any time \(t<T\), and it is calculated as spot price \((S_t)\) minus the present value of the exercise price:
$$c_t=\text{max}(0,S_t-X(1+r)^{-(T-t)}$$
Conversely, for the put option, the exercise value at any time \(t<T\) is given by;
$$p_t=\text{max}((0, X(1+r)^{-(T-t)}-S_t)$$
Assuming that \(X=F_0(T)\) and ignoring the upfront option premium, the exercise value of a call option is equivalent to the value of the long forward commitment at time \(t\) only if the spot price is greater than the present value of X.
That is, if \(S_t>PV(X)\), then:
$$S_t-PV(F_0(T))=\text{max}(0,S_t-PV(X))$$
Recall that the moneyness of an option is the relationship between the total value of an option and its exercise price. The best way to understand the concept of moneyness is via a graphical example. Below, you can see an example for a USD 150 call option. The green line represents when the option is in the money, and the blue represents times when the option is out of the money. The inverse would be true for a USD 150 put option. For both call and put options, the option is at the money when the line switches from blue to green.
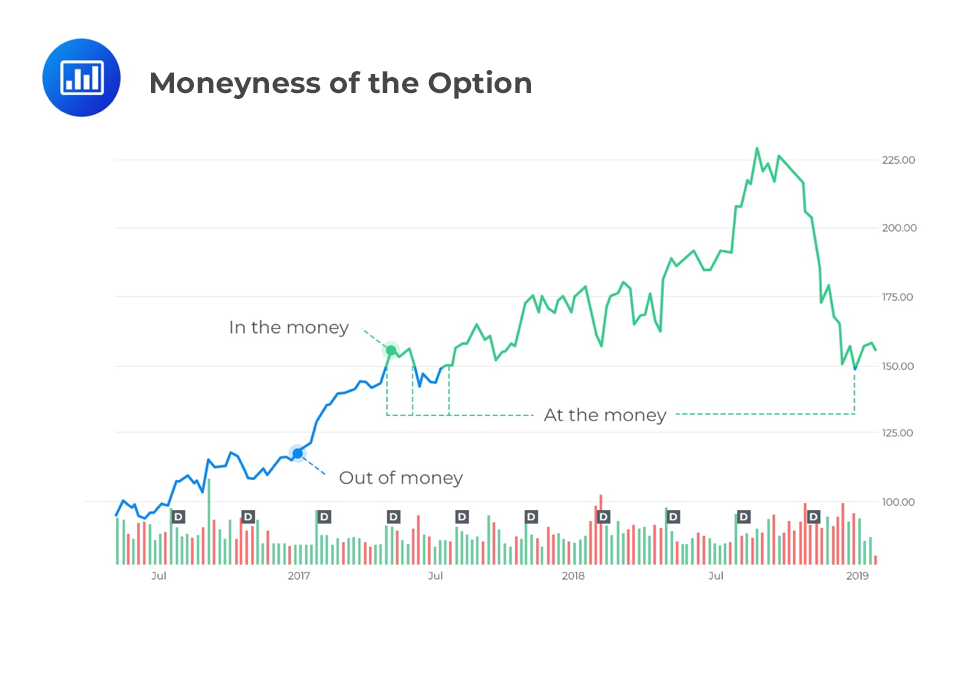
A call is said to be in the money if the underlying spot price is above the exercise price. That is, \(S_t>X\).
On the other hand, a put is in the money if the spot price is less than the exercise price. That is, \(S_t<X\).
In addition, an option is said to be deep in the money if it is highly exercisable, meaning the stock price is much higher than the exercise price.
A call is out of the money if the spot price exceeds the current exercise price. That is, \(S_T<X\).
On the other hand, a put is out of the money if the spot price is higher than the current exercise price \(S_T>X\).
An option is said to be deep out of the money if it is unlikely to be exercised, for example, if the stock price is USD 1 and the call option’s strike price is USD 50.
A call or a put is called at the money if the option’s exercise price equals the current underlying spot price. That is, \(S_t=X\).
The moneyness of an option can be summarized in the table below:
$$\small{\begin{array}{c|c|c}\textbf{Moneyness}&\textbf{Call Options}&\textbf{Put Options}\\ \hline \text{In the Money (ITM)}&S_t>X&S_t<X\\ \hline \text{At the Money (ATM)}&S_T=X&S_T=X\\ \hline \text{Out of the Money (OTM)}&S_t<X&S_t>X \end{array}}$$
Consider a 2-year call option with an exercise price of USD 100 and a risk-free rate of 2.31%. If, in six months, the underlying spot price is USD 98, the exercise value is closest to:
$$\begin{align*}c_t&=\text{max}(0,S_t-X(1+r)^{-(T-t)}) \\&=\text{max}(0,98-100(1.0231)^{-1.5})\\&=\text{max}(0,98-96.63)\\&=\text{USD 1.37}\end{align*}$$
European options are only exercised at the expiration date. However, they can be purchased or sold before maturity at a price that captures the option’s future expected payoff.
Denote the price by \(c_t\) for the call option and \(p_t\) for a put option. The time value of an option is defined as the difference between the current option price and the option’s current payoff (or exercise value).
For a call option, the time value is given by:
$$\text{Time value}=c_t-\text{max}(0, S_t-X(1+r)^{-(T-t)})$$
We can rearrange this so that:
$$c_t=\text{max}(0,S_t-X(1+r)^{-(T-t)})+\text{Time value}$$
For a put option, the time value is given by:
$$p_t=\text{max}(0,X(1+r)^{-(T-t)}-S_t)+\text{Time value}$$
From the formulas above, it is easy to see that the current option price equals the exercise value plus the time value for both call and put options:
$$c_t=\text{Exercise value}+\text{Time value}$$ $$p_t=\text{Exercise value}+\text{Time value}$$
Consider a 2-year call option with an exercise price of USD 100 and a risk-free rate of 2.31%. If, in six months, the spot price of the underlying is USD 98 and the price of the option is USD 1.88, the option’s time value is closest to:
$$\begin{align*} c_t&=\text{Exercise value}+\text{Time value} \\ \text{Time value}&=c_t-\text{Exercise value} \\ &=c_t-\text{max}(0,S_t-X(1+r)^{T-t})\\&=1.88-1.37\\&=\text{USD 0.51}\end{align*}$$
Question
A European put option on an underlying stock has four months to maturity. The option’s exercise price is USD 60. At option’s maturity, the underlying price is USD 53. The underlying has no associated cost of carry.
If the risk-free rate is 1.5% and the current option price is USD 3, the time value of the option is closest to:
A. $0.
B. -$3.703.
C. $3.00.
Solution
The correct answer is B.
The time value of a put option is given by:
$$\begin{align*}p_t&=\text{Exercise value}+\text{Time value} \\ \text{Time value}&=p_t-\text{Exercise value} \\ &=p_t-\text{max}(0,X(1+r)^{-(T-t)}-S_t)\\&=3-\text{max}((0,60(1.015)^{-\frac{4}{12}}-53)\\&=3-\text{max}(0,6.703)\\&=3-6.703\\&=-3.703\end{align*}$$
A is incorrect. It is the payoff of the put option,four months to maturity:
$$\begin{align*}\text{Payoff}&=\text{max}(0,X(1+r)^{-(T-t)}-S_t)\\&=\text{max}(0,53(1.015)^{-\frac{4}{12}}-60)\\&=0\end{align*}$$
C is incorrect.Calculates the payoff of the put option as:
$$\begin{align*}\text{Time value}&=p_t-\text{max}(0,X(1+r)^{-(T-t)}-S_t)\\&=3-\text{max}(0.53(1.015)^{-\frac{4}{12}}-60)\\&=3-\text{max}(0,-7.2624)\\&=3+0\\&=3\end{align*}$$