Determining the Value at Expiration and Profit from a Long or a Short Position in a Call or Put Option

Define the following:

\(c_T =\) Value of the call at expiration.

\(p_T =\) Value of a put option at expiration.

\(S_T =\) Price of the underlying at time T.

\(X =\) Exercise price.

\(c_0=\) Call option premium.

\(p_0 =\) Put option premium.

\(\Pi =\) Profit from an option strategy.

Payoff Profile of a Call Option

Recall that in call options, the buyer has the right but not the obligation to buy the underlying. Moreover, the call option will only be exercised if the payoff is positive; otherwise, the option expires worthless, and the option buyer incurs a loss equal to the option premium.

Intuitively for a call option, the buyer would only exercise the option if \(S_T>X\). As such, the payoff to the buyer at expiration is given by:

$$\text{C}_{\text{T}}=\text{max}(0,\text{S}_{\text{T}}-\text{X})$$

Conversely, the payoff to the seller at expiration is:

$$-\text{C}_{\text{T}}=-(\text{max}(0,\text{S}_{\text{T}}-\text{X}))$$

Note also that the option buyer pays the seller the call option premium (\(c_0\)) at time \(t=0\) for the right to buy the underlying \(S_T\) at an exercise price of \(X\) at time \(t=T\). Therefore, the profit the buyer will earn is calculated as follows:

$$\Pi =\text{max}(0,\text{S}_{\text{T}}-\text{X})-\text{C}_0$$

For the call option seller’s profit, it is given by:

$$\Pi =-\text{max}(0,\text{S}_{\text{T}}-\text{X})+\text{C}_0$$

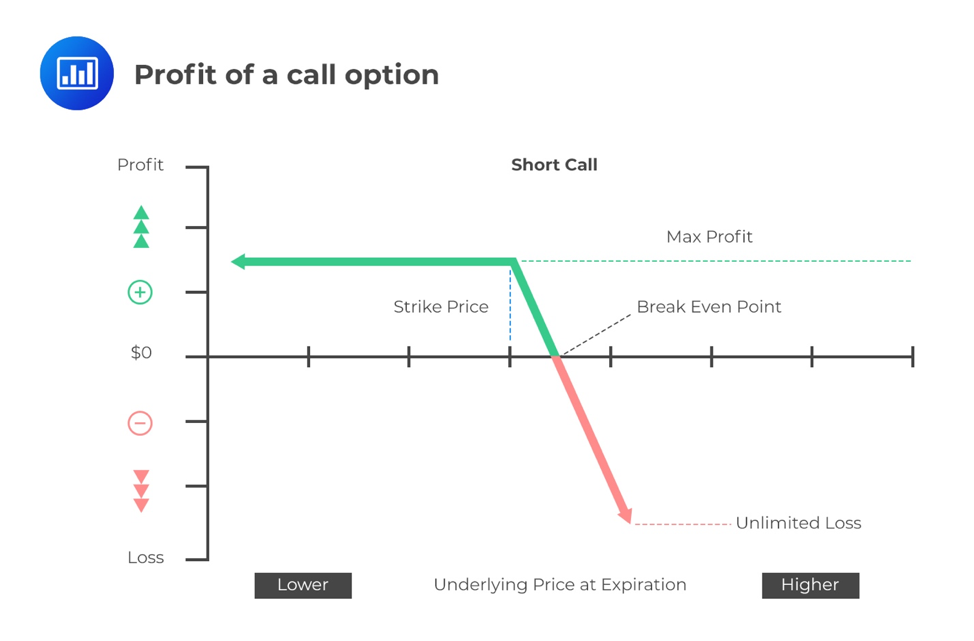
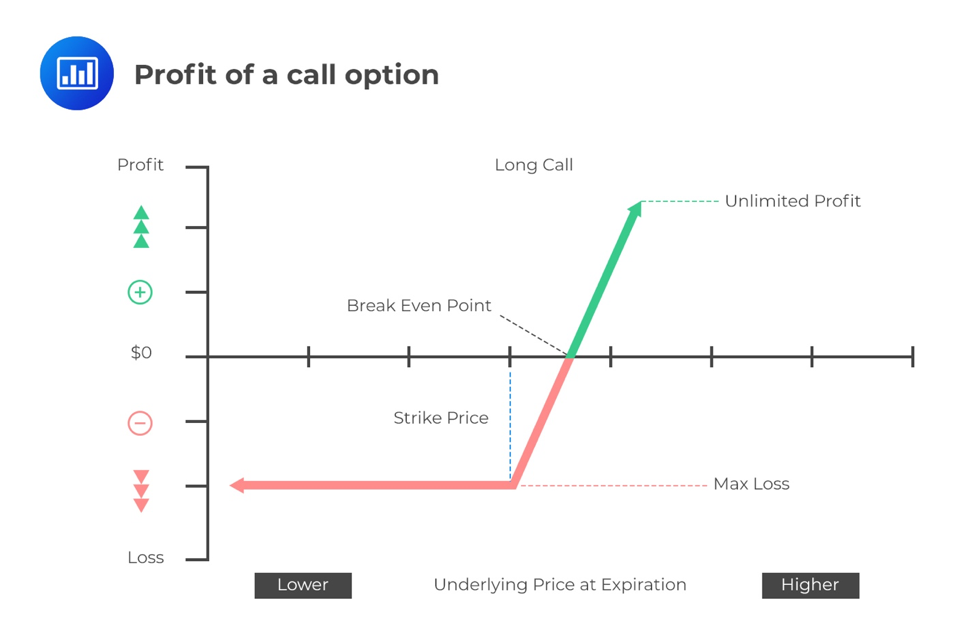
From the above graphs, the following points can be deduced:

• The maximum loss for the long (buyer) of the call option is the premium, and the profit for the buyer is unlimited.
• The maximum loss for the short (seller) of the call option is unlimited, and the greatest profit the seller can make is the premium.
• The breakeven point for both the long (buyer) and short (seller) is the strike price plus the premium.
• The sum of the profits between the long and the short equals zero since options trading is a zero-sum game.

Example: Calculating the Value (Payoff) of a Call Option at Expiration

Consider a one-year call option with a premium of $2 and a strike price of $30. If the price of the underlying at expiration is $40, the value at expiration is closest to:

Solution

At $40, the stock price is above the exercise price. Therefore, the option has a value of:

$$\begin{align*}c_T&=\text{max}(0, S_T-X)\\&=\$40-\$30\\&=\$10\end{align*}$$

Example: Calculating the Profit/Loss of a Call Option at Expiration

Consider a one-year call option with a premium of $2 and a strike price of $30. If the price of the underlying at expiration is $40, the value and profit/loss at expiration is closest to:

Solution

The buyer of the call option will exercise the option and make a profit of:

$$\begin{align*}\Pi &=\text{max}(0,\text{S}_{\text{T}}-\text{X})-\text{C}_0\\&=\$10-\$2\\&=\$8\end{align*}$$

Intuitively the seller is at a loss of:

$$\begin{align*}\Pi &=-\text{max}(0,\text{S}_{\text{T}}-\text{X})+\text{C}_0\\&-10+2\\&-\$8\end{align*}$$

Payoff Profile of a Put Option

For a put option, the buyer has the right but not an obligation to exercise the option at expiry. Exercising the option means that at expiration, the buyer sells the underlying \(S_T\) at the exercise price X. As such, the put option is only exercisable if \(S_T <X\).

Therefore, the payoff to the buyer is given by:

$$p_T=\text{max}(0,X-S_T)$$

Conversely, the payoff to the put option seller is:

$$-p_T=-(\text{max}(0,X-S_T))$$

Recall that the put option buyer pays the seller a put option premium (\(p_0\)).  Therefore, the profit to the option buyer is given by:

$$\Pi =\text{max}(0,\text{S}_{\text{T}}-\text{X})-\text{p}_0$$

Conversely, the profit to the options’ seller is given by:

$$\Pi =-\text{max}(0,\text{S}_{\text{T}}-\text{X})+\text{p}_0$$

The following graphs can represent the profit of a put option to both buyer and the seller:

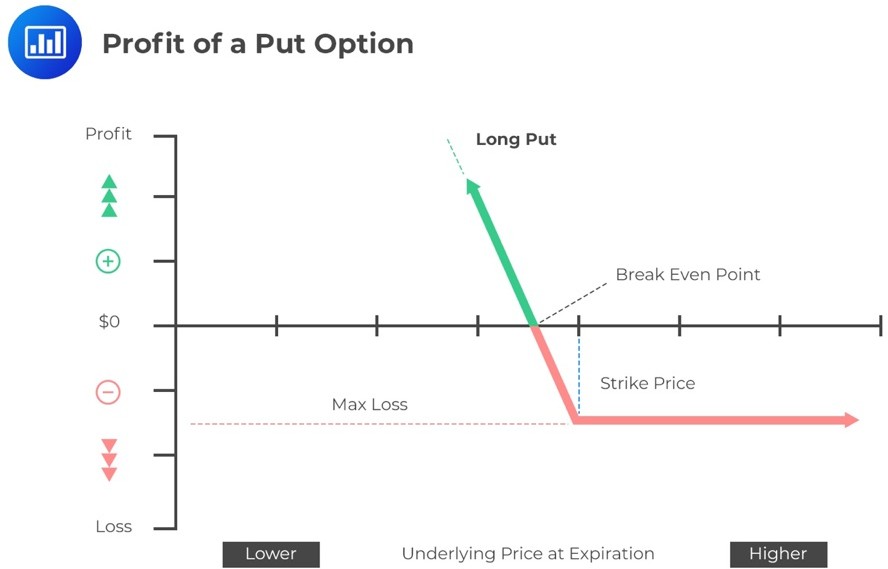
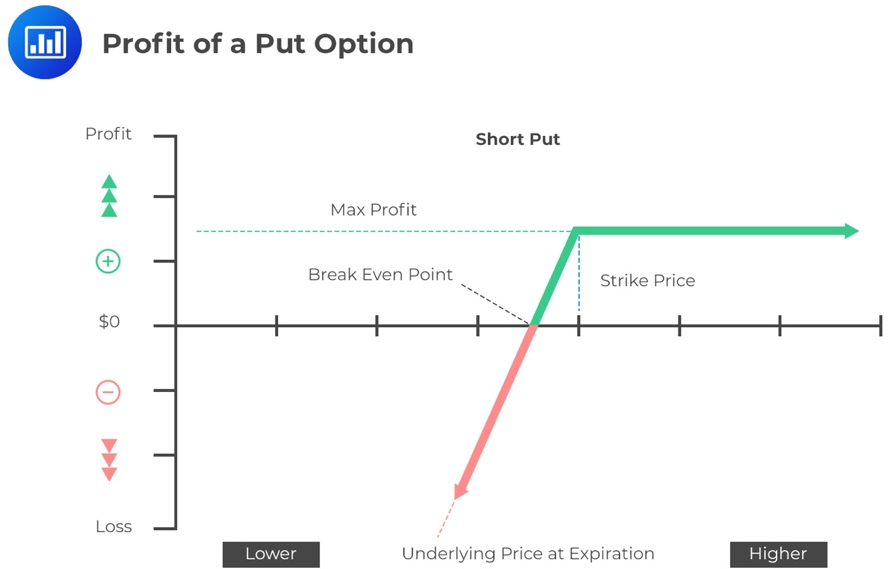
From the above graphs and formulas, the following can be deduced:

• The maximum loss for the long (buyer) of the put option is the premium paid, and the profit for the buyer is limited to the difference between the strike price and the underlying asset’s price (or strike price if the underlying price falls to 0) at expiration. The price of the underlying asset cannot drop below zero, so the maximum profit for the buyer cannot be unlimited.
• The maximum loss for the short (seller) of the put option is limited to the strike price, and the greatest profit the seller can make is the premium.
• The breakeven point for both the long (buyer) and short (seller) is the strike price minus the premium.
• The sum of the profits between the long and the short party equals zero. Options trading is a zero-sum game.

Example: Calculating the Payoff (Value) and Profit/Loss of Put Options

Consider a one-year put option with a premium of $3 and a strike of $30. If the underlying price at expiration is $20, the value and profit/loss at expiration is closest to:

Solution

At $20, the stock price is below the exercise price. Therefore, the options have a value of:

$$\begin{align*}p_T&=\text{max}(0,X-S_T)\\&=\$30-\$20\\&=\$10\end{align*}$$

The buyer of the put option will exercise the option; therefore, he makes a profit of:

$$\begin{align*}\Pi &=\text{max}(0,\text{X}-\text{S}_{\text{T}})-\text{p}_0\\&=\$10-\$3\\&=\$7\end{align*}$$

The seller/writer makes a loss of:

$$\begin{align*}\Pi &=-(\text{max}(0,X-\text{S}_{\text{T}}))+\text{p}_0\\&=-\$10+\$3\\&=-\$7\end{align*}$$

Question

If a put option has a premium of $3 and the exercise price is $100, and the price of the underlying is $105, the value at expiration and the profit to the option seller are closest to:

A. Value = -$3; Profit = $0

B. Value = $0; Profit = $8

C. Value = $0; Profit = $3

Solution

The correct answer is C.

Note that the exercise price ($100) is less than the underlying price ($105), so we have a situation where \(S_T\geq\text{X}\). Therefore, the option expires worthless, so the value (payoff) at maturity is zero (\(p_T=0\)).

Intuitively, the profit to the seller is equal to the option premium paid by the option buyer (\(\Pi =p_0\)), which is $3. From the perspective of the put buyer (long put),  \(p_T=0\) and \(\Pi =-p_0\) or a loss of $3.