Comparison of Swaps and Forward Contracts

Recall that a swap is a derivative contract between two counterparties to exchange a series of future cash flows. In comparison, a forward contract is also an agreement between two counterparties to exchange a single cash flow at a later date.  A single-period swap can, therefore, be considered a single-forward contract.

Swaps and forward contracts are similar in that both are forward commitments with symmetric payoff profiles. Besides, in both interest swaps and forward contracts, no cash exchanges hand at initiation.

A distinguishing factor, however, is that the fixed swap rate is constant, while a series of forward contracts have different forward rates at each expiration.

Forward Rate Agreement and Interest Rate Swaps

A forward rate agreement (FRA) is a cash-settled over-the-counter (OTC) contract between two counterparties. In this contract, the buyer (long position) is borrowing a notional sum (underlying) at a fixed interest rate (the FRA rate) and for a specified period starting at an agreed-upon date.

The seller deposits interest based on the market reference rate (MRR), where the MMR is established before the settlement dates, at time \(t-A\).

The FRA settlement amount is a function of the difference between the forward interest rate \((IFR_{A, B-A})\) and the market reference rate \((MRR_{B-A})\) or the MMR for \(B-A\) periods.

$$\text{Net payment}=(MRR_{B-A}-IFR_{A, B-A})\times\text{Notional principal}\times\text{Period}$$

Interest Rate Swaps

In a swap contract, two parties agree to exchange a series of cash flows. In the agreement, one party pays a variable (floating) series of cash flows that will be determined by a market reference rate (MRR) that resets every period. The other party pays either (1) a variable series based on a different underlying asset or rate or (2) a fixed series.

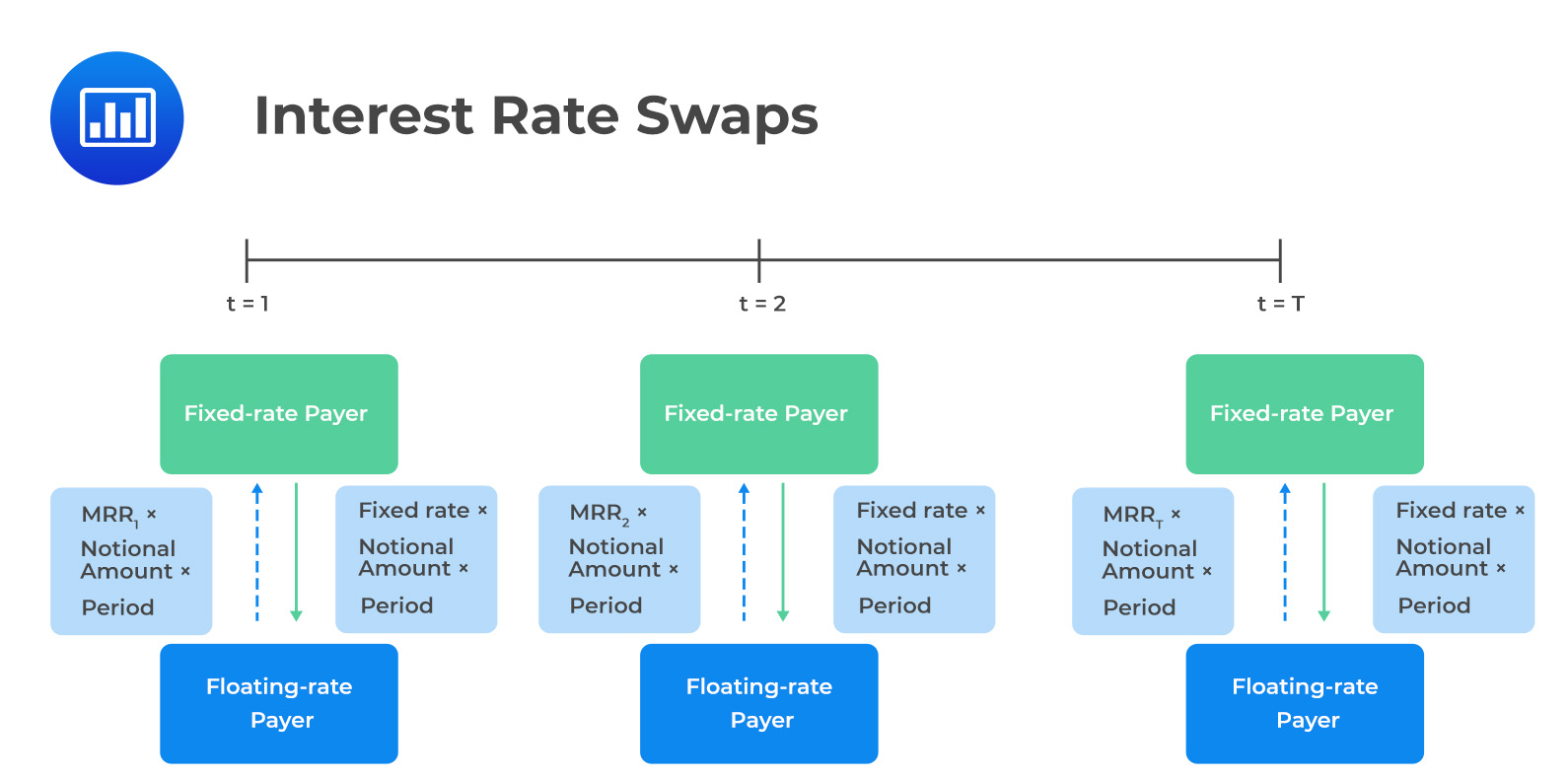
Note that, like a single-period swap, a forward rate agreement (FRA) consists of a single cash flow. As such, a multi-period swap can be viewed as a series of forward rate agreements.

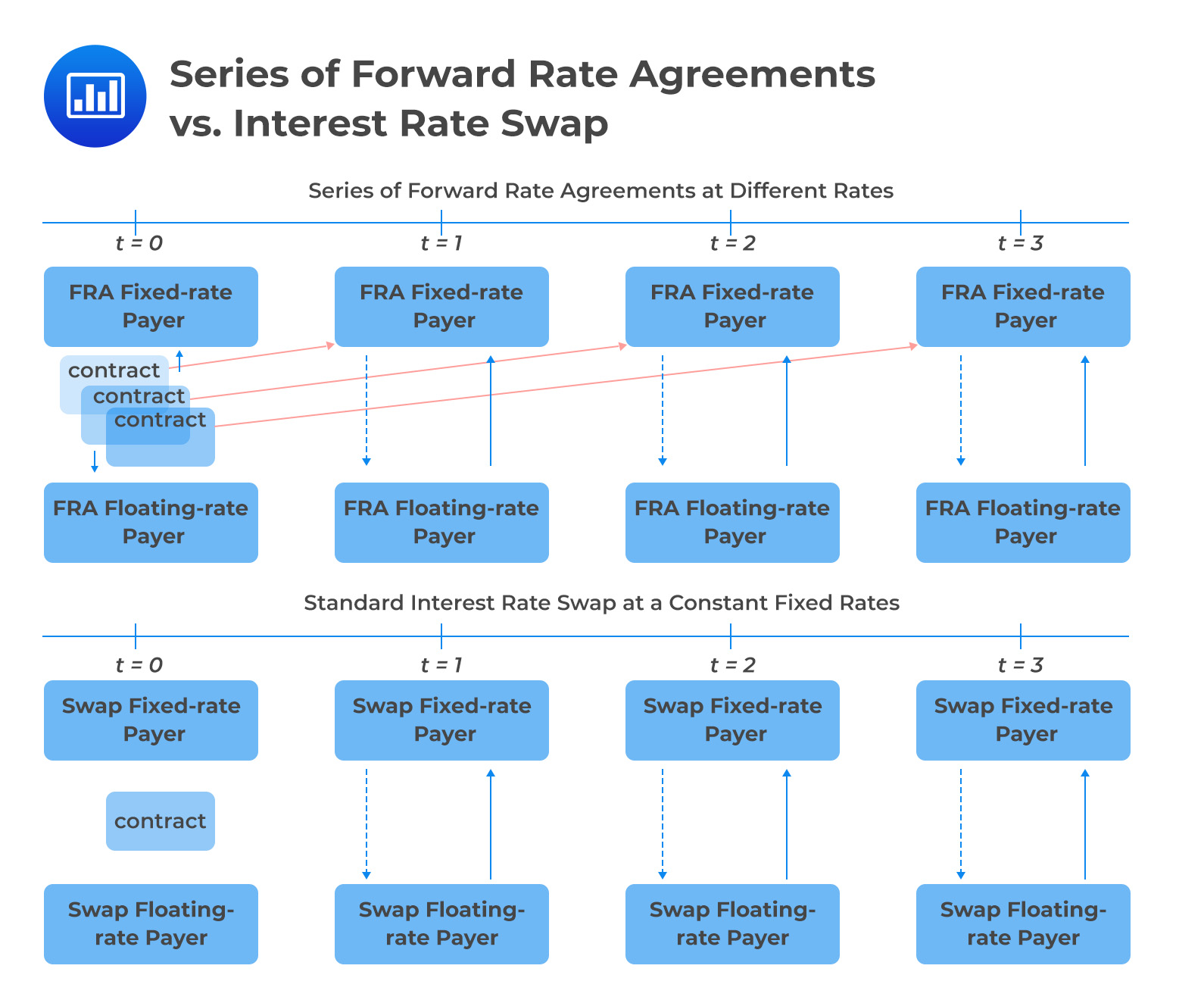
In single-period swaps and FRAs, the net difference between the fixed rate agreed on at inception and the market reference rate set in the future is used as the basis for determining cash settlement. Further, note that both FRAs and interest swaps have symmetric payoff profiles, no upfront cash at contract initiation, and counterparty credit exposure.

However, an FRA’s single settlement is done at the beginning of the period, while in interest swap rate, periodic settlements occur at the end of the respective period. In addition, looking at a swap as a series of FRAs, we would have a different fixed rate for each future time period. In the case of an interest rate swap, the fixed rate set today would apply throughout the period of the contract.

Par Swap Rate

Note that a standard interest rate swap involves an exchange of fixed payments at a constant rate for a series of floating-rate cash represented by the implied forward rates (IFR) at time \(t=0\).

The par swap rate is a fixed rate that equates the present value of all future expected floating cash flows to the present value of fixed cash flows. That is,

$$\sum^{N}_{i=1}\frac{IFR}{(1+Z_i)^i}=\sum_{i=1}^{N}\frac{S_i}{(1+Z_i)^i}$$

Where:

\(IFR=\) Implied forward rates.

\(s_i=\) Par swap rate for period \(i\).

\(z_i=\) Spot rates for period \(i\).

Example: Solving Par Swap (Fixed) Rate

A three-year bond has the following characteristics: $$\small{\begin{array}{c|c|c|c|c}\textbf{Years to Maturity} & \textbf{Annual Coupon} & \textbf{PV (per 100 FV)} & \textbf{Zero Rates} \\ \hline 1 & 1.25\% & 99.016 & 2.2565\% \\ \hline 2 & 2.5\% & 98.634 & 3.2282\% \\ \hline 3 & 3.0\% & 97.222 & 4.0354\% \end{array}}$$

Determine the par swap (fixed) rate for a three-year contract and the fixed rate for each of the three one-year FRAs that would match the single three-year swap.

We already have the one-year forward rate at \(t=0\) i.e., \(IFR_{0,1}=2.2565\%\). We need to determine the implied one-year forward rates (IFR) at \(t=1\) and \(t=2\).

$$(1+z_A)^A\times(1+IFR_{A, B-A})^{B-A}=(1+z_{B})^B$$

Therefore, solving for \(IFR_{1,1}\)

$$\begin{align*}(1+0.022565)^1\times(1+IFR_{1,1})^1&=(1+0.032282)^2\\ \rightarrow \text{IFR}_{1,1}&=\frac{1.032282^2}{1.022565}-1\\&=0.042091\end{align*}$$

and \((1+IFR_{2,1})^1\).

$$\begin{align*}(1+0.032282)^2\times(1+IFR_{2,1})^1&=(1+0.040354)^{3}\\ \rightarrow \text{IFR}_{2,1}&=\frac{1.040354^3}{1.032282^2}-1\\&=0.056688\end{align*}$$

Consider the following table:

$$\small{\begin{array}{c|c|c|c|c} \textbf{Years to Maturity} & \textbf{Annual Coupon} & \textbf{PV (per 100 FV)} & \textbf{Zero Rates} & \textbf{IFR} \\ \hline 1 & 1.25\% & 99.016 & 2.2565\% & 2.2565\% \\ \hline 2 & 2.5\% & 98.634 & 3.2282\% & 4.2091\% \\ \hline 3 & 3.0\% & 97.222 & 4.0354\% & 5.6688\% \end{array}}$$

In this case, the par swap rate, is the fixed rate that equates the present value of all future expected floating cash flows to the present value of fixed cash flows:

$$\sum^{N}_{i=1}\frac{IFR}{(1+Z_i)^i}=\sum_{i=1}^{N}\frac{S_i}{(1+Z_i)^i}$$

$$\begin{align*}\rightarrow\frac{2.2565\%}{1.022565}+\frac{4.2091\%}{1.032282^2}+\frac{5.6688\%}{1.040354^3}&=\frac{s_3}{1.022565}+\frac{s_3}{1.032282^2}+\frac{s_3}{1.040354^3}\\0.11191&=2.80445s_3\\ \therefore \text{s}_3&=\frac{0.11191}{2.80445}\\&=0.03990\approx 3.99\%\end{align*}$$

The three-year swap rate of 3.99% may be interpreted as a multi-period breakeven rate, or the rate at which an investor would be indifferent to:

• Paying the fixed swap rate and receiving the respective forward rates.
• Receiving the fixed swap rate and paying the respective forward rates. 

Question

Which of the following most likely distinguishes forward rate agreements and interest rate swaps?

A. Fixed rate at each period.

B. Symmetric payoff profiles.

C. Netting of payments in each period.

Solution

The correct answer is A.

Considering a swap as a series of FRAs, we would have a different fixed rate for each future time period. On the other hand, in an interest rate swap, the fixed rate set today would apply throughout the period of the contract.

Remember that interest rates are characterized by term structure, and, as such, we would expect FRAs to have fixed rates for different times to maturity.

B is incorrect. Both FRAs and interest rate swaps have symmetric payoff profiles.

C is incorrect. In single-period swaps and FRAs, the net difference between a fixed rate agreed on at inception, and an MRR (market reference rate) set in the future is used to determine cash settlement on a given notional principal over the specified time period.