Put-Call Parity for European Options

Although parity means equivalence, puts and calls are not equivalent. However, there is a relationship between the price of a call and its corresponding put option. This is referred to as put-call parity.

Protective Puts and Fiduciary Calls

First, let’s consider a protective put strategy where an investor who holds the underlying asset purchases a protective put option. At inception, the investor commits S₀, the underlying asset cost, and p₀, the put premium.

$$ \text{Value at inception} = p_0 + S_0 $$

A protective put gives the holder a limited downside but reduces his upside a bit because of the cost paid to buy the put option. Graphically, it can  be represented as:

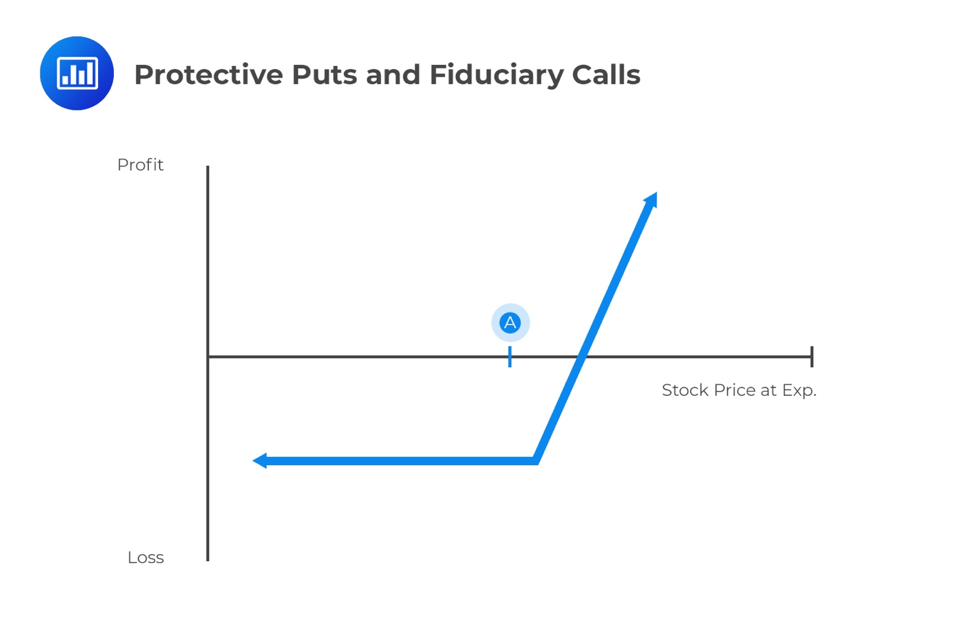
A strategy where an investor enters into a fiduciary call means an investor buys a call option on an underlying asset and a risk-free zero-coupon bond with a face value equal to the exercise price.

$$ \text{Value at inception} = c_0 + \frac{X}{(1+r)^T} $$

The payoff graph from this strategy will be the exact same as that of the protective put strategy.

Put-Call Parity Arbitrage

By examing the payoff profiles of a protective put and a fiduciary call, we note that they are identical. Therefore, if two combinations of assets or portfolios of assets have the same payoff, their acquisition cost must be identical. In any other case, there is an arbitrage opportunity. In other words, someone can make a risk-free profit by buying the cheaper one and selling the most expensive one.

As a result of the no-arbitrage principle, we can set the value at the inception of the protection call equal to the value at the inception of the protective put as follows:

$$ c_0 + \frac{X}{(1+r)^T} = p_0 + S_0 $$

This equation is a key concept in derivatives pricing called put-call parity. This formula equates the value of calls and puts through equivalent portfolios. It must be assumed that since these are European options, they have the same strike, same expiry date, and the same underlying asset.

By re-arranging the prior equation:

$$ c_0  = p_0 + S_0 – \frac{X}{(1+r)^T} $$

The right side of this equation is equivalent to a call option and is referred to as a synthetic call. It consists of a long put, a long position in the underlying asset, and a short position in the risk-free bond.

Another re-arrangement can be made to isolate the put option:

$$  p_0 = c_0 +\frac{X}{(1+r)^T} – S_0  $$

The right side of this equation is now referred to as a synthetic put which consists of a long call, a short position in the underlying, and a long position in the risk-free bond.

Question

European put and call options both have an exercise price of $50 that expires in 120 days. The underlying asset is priced at $52 and makes no cash payments during the life of the option. The risk-free rate is 4.5% and the put is selling for $3.80. According to the put-call parity, the price of the call option should be closest to:

A. $6.52

B. $6.32

C. $7.12

Solution

The correct answer is A.

c₀ = p₀ + S₀ – X/(1+r)^T

c₀ = 3.80 + 52 – (50/1.045^120/365) = 6.52