Interest Rates Forward Contracts

The link between the spot and forward prices is determined by a risk-free interest rate which is regarded as the opportunity cost of holding an asset. Term structure implies that various interest rates are available depending on the time to maturity. Given an upward-sloping yield curve, which is the most usual case, investors would charge a higher yearly interest rate for five-year loans than for a one-year loan.

Spot Rates

A spot rate, also known as zero rates, is defined as the yield to maturity of a zero-coupon security maturing at the date of each cash flow.

Example: Spot Rate

A 4-year $2,000 par value bond pays 10% annual coupons. The spot rate for year 1 is 8%, the 2-year spot rate is 13%, the 3-year spot rate is 14%, and the 4-year spot rate is 16%. The price of the bond is closest to:

Solution

Here, we have an upward-sloping yield curve since the 2-, 3-, and 4-year interest rates are higher than the 1-year interest rate.

$$\begin{align*}\text{Annual coupon}&=$2000\times10\%=$200\\ \text{Price}&=\bigg(\frac{\$200}{(1.08)^1}\bigg)+\bigg(\frac{\$200}{(1.13)^2}\bigg)+\bigg(\frac{\$200}{(1.14)^3}\bigg)+\bigg(\frac{\$2200}{(1.16)^4}\bigg)\\&=\$1691.85\end{align*}$$

Discount Factor

The discount factor is the price equivalent of a zero/spot rate, which, when multiplied by the total amount of money to be received (principal + interest), gives the bond’s price (present value).

$$\text{Discount factor}\ (DF_i)=\frac{1}{(1+\text{Discount rate} (Z_i))^{\text{Period number}(i)}}$$

Example: Discount Factor

Suppose that an investor sells a four-year zero-coupon bond at par with a price of 94.78; the four-year zero rates is closest to:

Solution

$$\text{DF}_i=\frac{1}{(1+Z_i)^i}$$

Where:

\(DF_i=\) The discount factor for a given period.

\(Z_i=\) The zero rate for a given period.

\(i=\) The period.

To solve for the four-year zero rate \(z_4\) solve the equation:

$$94.78=\frac{100}{(1+z_4)^4}$$

We can see that:

$$\begin{align*}0.9478&=\frac{1}{(1+z_4)^4}\\Z_4&=0.013493\approx1.3493\%\end{align*}$$

Forward Rates vs. Spot Rates

A forward rate indicates the interest rate on a loan beginning at some time in the future. A spot rate, on the other hand, is the interest rate on a loan beginning immediately.

In an interest rate forward contract, the most common market practice is to name forward rates. For instance, “3y7y” is also denoted as \(F_{3,7}\), which means “3-year into 7-year rate”. The first number refers to the length of the forward period from today, while the second one refers to the tenor or time-to-maturity of the underlying bond.

For short-term market reference rates (MRRs), forward rates are normally named in months. For example, (F_{2m,5m}\) means the 5-month forward period starting at the end of 2 months, and the time-to-maturity is seven months from today.

Implied Forward Rate (IFR)

The implied forward rate is the breakeven rate that links a short-date and long-dated zero-coupon bond. It is an interest rate at a future period where an investor breaks even and can earn the same return as today.

The general formula for the relationship between the two spot rates and the implied forward rate (IFR) is:

$$(1+Z_B)^B=(1+Z_A)^A\times(1+IFR_{A,B-A})^{B-A}$$

Where:

\(Z_{A}=\) Yield-to-maturity per period of short-term bond.

\(Z_{B}=\) Yield-to-maturity per period of long-term bond.

\(IFR_{A, B-A}=\) Implied forward rate between period A and period B, with a tenor of B-A.

The implied forward rate (IFR) is the interest rate for a period in the future where an investor can earn a return:

• By investing now until the forward rate reaches its final maturity.
• By investing now until the forward rate’s start date. Besides, the investor increases returns at the implied forward rate by rolling over the proceeds.

Example: Implied Forward Rate

An investor notes that the two-year and the three-year zero-coupon bonds yield 6% and 8%, respectively. The investor enters a one-year fixed-rate FRA agreement to hedge against rate fluctuations.

The implied forward rate applicable to the investor’s position is closest to:

Solution

$$\begin{align*}(1+Z_A)^A\times(1+IFR_{A,B-A})^{B-A}&=(1+Z_B)^B\\ (1.06)^2\times(1+IFR_{2,1})^1&=(1.08)^3\\ 1.1236\times(1+IFR_{2,1})&=1.2597\\ 1.1236+1.1236IFR_{2,1}&=1.2597\\ 1.1236IFR_{2,1}&=0.136112\\IFR_{2,1}&=\frac{0.136112}{1.1236}\\&=0.1211\approx12.11\%\\ \end{align*}$$

Forward Rate Agreements (FRAs)

A forward rate agreement (FRA) is a cash-settled over-the-counter (OTC) contract between two counterparties. In this contract, the buyer (long position) is borrowing and the seller (short position) is lending a notional sum (underlying) at a fixed interest rate (the FRA rate) and for a specified period starting at an agreed date, e.g., period A in the future and ends in period B.

The seller deposits interest based on the market reference rate (MRR), where the MMR is established before the settlement dates, at time \(t=A\).

The FRA settlement amount is a function of the difference between the forward interest rate \((IFR_{A, B-A})\) and the market reference rate \((MRR_{B-A})\) or the MMR for \(B-A\) periods, which ends at period B.

FRAs are usually cash-settled at the beginning of the period during which the reference rate applies.

The net payment from the long position’s perspective would be:

$$\text{Net payment}=(MRR_{B-A}-IFR_{A,B-A})\times\text{Notional principal}\times\text{Period}$$

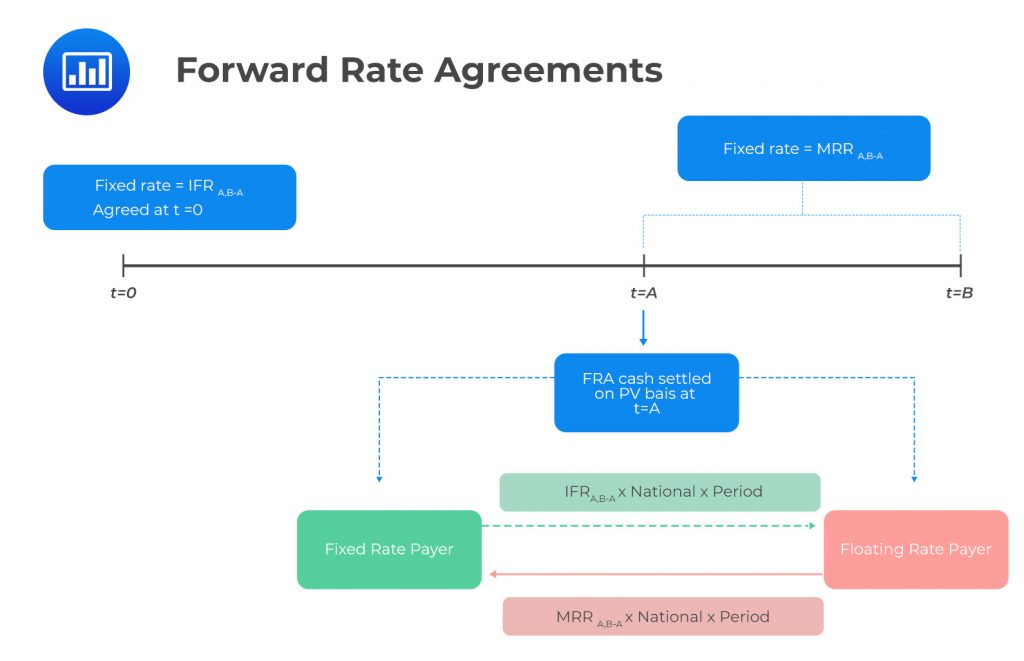
FRA can be seen as a one-period interest swap. They are mainly utilized by investors and issuers to manage interest rate risk. The notional amount is not exchanged but used for interest calculations. Also, fixed and floating payments occur on a net basis. Financial intermediaries use FRAs to protect rate-sensitive balance sheets, assets, or liabilities against interest rate risk.

Example: Forward Rate Agreements

James Malcolm enters an FRA agreement with Fred Green on a notional amount of USD 50,000. Malcolm will receive a fixed rate in 4 months, and a two-month MRR is set at 1.3%. If the \(IFR_{3m,1m}\) at the initiation of the contract is 2.5%, the settlement amount is closest to:

Solution

$$\begin{align*}\text{Net payment at the end of the period}&=(MRR_{B-A}-IFR_{A,B-A})\times\text{Notional principal}\times\text{Period}\\&=(2.5\%-1.3\%)\times\text{USD 50,000}\times\frac{2}{12}\\&=\text{USD 100}\end{align*}$$

$$\begin{align*}\text{Cash settlement (PV)}&=\text{USD}\frac{100}{1+0.013/12}\\&=\text{USD 99.89}\end{align*}$$

Question

Vanessa Raquela is an analyst at Money Wise Capital. She analyses two-year and three-year government zero-coupon bonds whose prices are 95 and 92 per 100 face value, respectively. The implied two-year forward rate in five years’ time is closest to:

A. 2.60%.

B. 2.81%.

C. 3.26%.

Solution

$$\text{DF}_{i}=\frac{1}{(1+Z_i)^i}$$

Thus:

$$\begin{align*}0.95&=\frac{1}{(1+z_2)^2}=2.5978\%\\0.92&=\frac{1}{(1+z_3)^3}=2.81845\%\end{align*}$$

Now we need to solve for \(IFR_{2,5}\) as follows:

$$\begin{align*}(1+Z_A)^A\times(1+IFR_{A,B-A})^{B-A}&=(1+Z_B)^B\\(1+Z_2)^2\times(1+IFR_{2,5})&=(1+z_3)^{3} \\1.025978^2\times(1+IFR_{2,5})&=1.0281845^{3}\end{align*}$$

Where:

$$\begin{align*}1.025978^2(1+IFR_{2,5})&=1.0281845^{3}\\ 1.025978^2(1)+(1.025978^2)(IFR_{2,5})&=1.0281845^{3}\\ 1.052631+1.052631 IFR_{2,5}&=1.086959\\ 1.052631 IFR_{2,5}&=0.034328\\IFR_{2,5}&=0.032612\approx3.2612\%\end{align*}$$