Use of Derivatives among Issuers
Financial intermediaries, investors, and issuers use derivative products to increase, reduce, or alter... Read More
Put-call parity is a no-arbitrage concept. It involves a combination of cash and derivative instruments in a portfolio. Put-call parity allows pricing and valuation of these positions without directly modeling them using non-arbitrage conditions.
Consider an investor whose main objective is to benefit from an increase in the underlying value and hedge an investment against a decrease in underlying value.
Consider the following portfolios:
At time \(t=0\), an investor buys a call option at a price of \(c_0\) on an underlying with an exercise price of \(X\) and a risk-free bond that is redeemable at \(X\) at time \(t=T\). Intuitively, assuming the call option expires at time t=T, the cost of this strategy is
$$c_0+X\left(1+r\right)^{-T}$$
In this portfolio, the investor buys a call option with a positive payoff if the underlying price exceeds the exercise price \((S_T>X)\) and invests cash in a risk-free bond. This strategy is called the fiduciary call.
At time \(t=0\), an investor buys an underlying at a price of \(S_0\) and a put option on the underlying price of \(p_0\) whose exercise price is \(X\) at time \(t=T\). Intuitively, the cost of this strategy is
$$p_0+S_0$$
The strategy applied in portfolio B is called protective put. Protective put involves holding an asset and buying a put on the same asset.
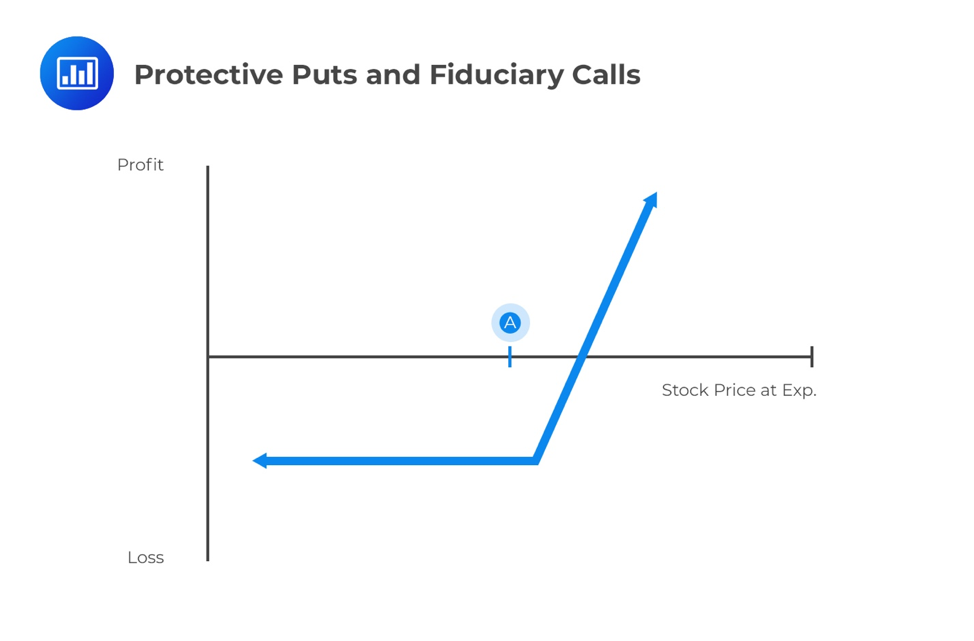
Both portfolios allow the investor to benefit from the rise in underlying price without exposure to a decrease below the exercise price. Moreover, portfolios A and B have identical profiles. Based on the no-arbitrage condition, assets with similar future payoff profiles must trade at the same price, ignoring associated transaction costs.
Consider the following table:
$$
\begin{array}{l|c|c|c}
\textbf { Portfolio Position } & \begin{array}{l}
\textbf { Put exercised } \\
\boldsymbol{S}_{\boldsymbol{T}}<\boldsymbol{X}
\end{array} & \begin{array}{l}
\textbf { No Exercise } \\
\boldsymbol{S}_{\boldsymbol{T}}=\boldsymbol{X}
\end{array} & \begin{array}{l}
\textbf { Call Exercised } \\
\boldsymbol{S}_{\boldsymbol{T}}>\boldsymbol{X}
\end{array} \\
\hline \textbf { Fiduciary Call: } & \\
\hline \text { Call Option } & 0 & 0 & S_T-X \\
\hline \text { Risk-free Asset } & X & X & X \\
\hline \text { Total: } & \boldsymbol{X} & \boldsymbol{X}\left(=\boldsymbol{S}_{\boldsymbol{T}}\right) & \boldsymbol{S}_{\boldsymbol{T}} \\
\hline \textbf { Protective Put: } \\
\hline \text { Underlying Asset } & S_T & S_T & S_T \\
\hline \text { Put option } & X-S_T & 0 & 0 \\
\hline \text { Total: } & \boldsymbol{X} & \boldsymbol{S}_{\boldsymbol{T}}(=\boldsymbol{X}) & \boldsymbol{S}_{\boldsymbol{T}} \\
\end{array}
$$
Therefore, since portfolios A and B have identical payoffs at time \(t=T\), the costs of these portfolios must be similar at time \(t=0\). For this reason, the put-call parity equation:
$$S_0+p_0=c_0+X\left(1+r\right)^{-T}$$
Where:
\(S_0 =\) Price of the underlying asset.
\(p_0=\) Put premium.
\(c_0=\) Call option premium.
\(X=\) Exercise price.
\(r=\) Risk-free rate.
\(T=\) Time to expiration.
Put-call parity holds for European options that have similar exercise prices and expiration times. These similarities ensure a no-arbitrage relationship between the put option, call option, the underlying asset, and risk-free asset prices. Put-call parity implies that at time \(t=0\), the price of the long underlying asset plus the long put must be equal to the price of the long call option plus the risk-free asset.
Consider European put and call options, where both have an exercise price of $50 and expire in 3 months. The underlying asset is priced at $52 and makes no cash payments during the life of the options.
If the put is selling for $3.80 and the risk-free rate is 4.5%, the price of the call option is closest to:
Solution
The put-call parity is given by:
$$S_0+p_0=c_0+X\left(1+r\right)^{-T}$$
We need to rearrange the formula to make the subject of the formula so that:
$$\begin{align}c_0 &=S_0+p_0-X\left(1+r\right)^{-T}\\&=52+3.80-50\left(1.045\right)^{-0.25}\\&=$6.35\end{align}$$
We can rearrange the put-call parity equation to solve for the put option premium, \(p_0\):
$$p_0=c_0+X\left(1+r\right)^{-T}-S_0$$
The right side of this equation is referred to as a synthetic put. It consists of a long call, a short position in the underlying, and a long position in the risk-free bond.
We can make another re-arrangement to solve for a long call, \(c_0\):
$$c_0=p_0+S_0-X\left(1+r\right)^{-T}$$
The right side of this equation is equivalent to a call option and is referred to as a synthetic call. It consists of a long put, a long position in the underlying asset, and a short position in the risk-free bond.
Also, we can further rearrange the put-call parity as follows:
$$S_0-c_0=X\left(1+r\right)^{-T}-p_0$$
The right-hand side of the above equation is called the covered call position. Intuitively, a covered call is equivalent to a long risk-free bond and short put option.
In summary, synthetic relationships with options occur by replicating a one-part position under put-call parity. Study the following table.
$$
\begin{array}{l|c|c|c|c}
\textbf { Position } & \begin{array}{c}
\textbf { Underlying } \\
\left(\boldsymbol{S}_{\mathbf{0}}\right)
\end{array} & \begin{array}{c}
\textbf { Risk-free Bond } \\
\left((\mathbf{1}+\boldsymbol{r})^{-T}\right)
\end{array} & \begin{array}{c}
\textbf { Call Option } \\
\left(\boldsymbol{c}_{\mathbf{0}}\right)
\end{array} & \begin{array}{c}
\textbf { Put Option } \\
\left(\boldsymbol{p}_{\mathbf{0}}\right)
\end{array} \\
\hline \text { Underlying }\left(\boldsymbol{S}_{\mathbf{0}}\right) & – & \text { Long } & \text { Long } & \text { Short } \\
\hline \begin{array}{c}
\text { Risk-free bond } \\
\left(\frac{x}{(1+r)^{\mathrm{T}}}\right)
\end{array} & \text { Long } & – & \text { Short } & \text { Long } \\
\hline \text { Call option }\left(\boldsymbol{c}_{\mathbf{0}}\right) & \text { Long } & \text { Short } & – & \text { Long } \\
\hline \text { Put Option }\left(\boldsymbol{p}_{\mathbf{0}}\right) & \text { Short } & \text { Long } & \text { Long } & – \\
\end{array}
$$
If the put-call parity does not hold, an arbitrage opportunity exists. The arbitrage opportunity can be exploited by selling the most expensive portfolio and purchasing the cheaper one.
Example: Arbitrage Opportunity
A European call option with a strike price of $25 sells at $7. The price of a European put option with the same strike price is also $7. If the underlying stock sells for $28, and the one-year risk-free rate is 4%, determine if there is an arbitrage opportunity.
Solution
The put-call parity equation:
$$\begin{align}p_0+s_0 & ≟ c_0+X(1+r)^{-T}\\7+28&≟7+25(1.04)^{-1}\\35 & \neq31.0385\end{align}$$
To exploit the opportunity, we need to:
We get a cash inflow of \($35-$31.0385=$3.9615\). Thus, the strategy provides cash inflow ($3.9615) today and no cash outflow at expiration.
Question
European put and call options have an exercise price of $50 and expire in four months. The underlying asset is priced at $52 and makes no cash payments during the option’s life. The risk-free rate is 4.5%, and the put is selling for $3.80. According to the put-call parity, the price of the call option should be closest to:
A. $5.25.
B. $6.35.
C. $7.12.
Solution
The correct answer is B.
The put-call parity is given by:
$$S_0+p_0=c_0+X\left(1+r\right)^{-T}$$
Where:
\(S_0\) =Price of the underlying asset.
\(p_0\) = Put premium.
\(c_0\)= Call option premium.
\(X\) = Exercise price.
\(r\)= Risk-free rate.
\(T\)= Time to expiration.
Making \(c_0\) the subject, we have:
$$\begin{align}c_0&=S_0+p_0-X\left(1+r\right)^{-T}\\&=52+3.80-50\left(1.045\right)^{-0.25}\\&=6.35\end{align}$$
Get Ahead on Your Study Prep This Cyber Monday! Save 35% on all CFA® and FRM® Unlimited Packages. Use code CYBERMONDAY at checkout. Offer ends Dec 1st.