Capital Allocation

Capital allocation describes the process companies use to make decisions on capital projects, i.e., projects with a lifespan of one year or more. It is a cost-benefit exercise that seeks to produce results and benefits greater than the costs of capital allocation efforts.

There are several steps involved in the capital allocation process. However, the specificity of the procedures a manager adopts depends on factors such as the manager’s position in the company, the size and complexity of the project being evaluated, and the company’s size.

Capital Allocation Process

The typical steps involved in the capital allocation process are:

1. Idea generation: Ideas can come from any source, but management must have a concrete grasp of the competitive environment in which the potential investment exists, along with the company’s current operations, competencies, and competitive position.
2. Investment analysis: Information is gathered, which helps forecast cash flows for each project and evaluate a project’s profitability.
3. Planning and prioritization: This involves looking at project timing, scheduling, prioritizing, and coordinating.
4. Monitoring and post-investment review: A project’s performance is assessed, and actual results (revenues, expenses, cash flows, etc.) are compared with planned or projected results.

Methods of Evaluating Capital Investments

Several essential decision criteria are used to evaluate capital investments. The two most comprehensive and well-understood measures of whether or not a project is profitable are the net present value (NPV) and the internal rate of return (IRR).

Moreover, Analysts can utilize consolidated financial statements to compute and evaluate the return on invested capital (ROIC). ROIC serves as a valuable overall return metric instead of a project-specific return measure.

Net Present Value (NPV)

The net present value (NPV) of a project is the potential change in wealth resulting from the project after accounting for the time value of money. The NPV for a project with one investment outlay made at the start of the project is defined as the present value of the future after-tax cash flows minus the investment outlay.

$$ \begin{align*}
NPV &= {CF}_0+\frac{{CF}_1}{{(1+r)}^1}+\frac{{CF}_2}{{(1+r)}^2}+\ldots+\frac{{CF}_T}{{(1+r)}^T} \\
NPV & =\sum_{t=0}^{T}\frac{{\rm CF}_t}{{(1+r)}^t}
\end{align*} $$

Where:

\({CF}_T\) = After-tax cash flow at time \(t\)

\(r\) = Required rate of return for the investment

\({CF}_0\) = Investment cash flow at time zero

Many projects have cash flow patterns in which outflows occur at the start of the project (at time = 0) and future dates. In these instances, a better formula to use is:

• to invest in the project if \(NPV \gt 0\);
• not to invest in the project if \(NPV \lt 0\); and
• stay indifferent if \(NPV = 0\).

In other words, positive NPV investments increase wealth, while negative NPV investments decrease wealth.

Example: Net Present Value of a Project

Suppose Company A is considering an investment of $100 million in a capital expansion project that will return after-tax cash flows of $20 million per year for the first three years and another $33 million in year 4, the project’s final year. If the required rate of return for the project is 8%, what would the NPV be, and should the company undertake this project?

$$ \begin{align*}
NPV & =-100+\frac{20}{{1.08}^1}+\frac{20}{{1.08}^2}+\frac{20}{{1.08}^3}+\frac{20}{{1.08}^4} \\
NPV & =-100+18.519+17.147+15.877+24.256 \\ & =-\$24.202 \text{ million} \end{align*} $$

Since the \(NPV \lt 0\), the project should not be undertaken.

Internal Rate of Return

The internal rate of return (IRR) is the discount rate that makes the net present value (NPV) of all cash flows from a particular project equal to zero. For a project with one initial outlay, the IRR is the discount rate that makes the present value of the future after-tax cash flows equal to the investment outlay.

The IRR solves the equation:

$$ NPV=\sum_{t=0}^{T}\frac{{CF}_t}{{(1+IRR)}^t}-\text{Outlay}=0 $$

It looks very much like the NPV equation except that the discount rate is the IRR instead of r, the required rate of return. Discounted at the IRR, the NPV is equal to zero.

The decision rule for the IRR is:

• to invest in the project if the IRR exceeds the required rate of return for the project, i.e., invest if \(IRR \gt r\); and
• not to invest if \(IRR \lt r\).

In instances where the outlays for a project occur at times other than time 0, a more general form of the IRR equation is:

$$ \sum_{t=0}^{T}\frac{{CF}_t}{{(1+IRR)}^t}=0 $$

Example: IRR of a project

Here is a follow-up on the above NPV example. If company A is considering an investment of $100 million in a capital expansion project that will return after-tax cash flows of $20 million per year for the first three years and another $33 million in year 4, the final year of the project, what is the IRR for this project and should it be undertaken given that the required rate of return for the project is 8%?

Solve IRR in the following equation:

$$ -100+\frac{20}{\left(1+IRR\right)^1}+\frac{20}{\left(1+IRR\right)^2}+\frac{20}{\left(1+IRR\right)^3}+\frac{33}{\left(1+IRR\right)^4}=0 $$

The solution can be arrived at through trial and error. However, a more straightforward approach is to use a financial calculator using the following steps:

Step 1: Entering the Initial Cash Outlay

Press the Cash Flow [CF] key to open the cash flow register. The calculator should read CF0=, which tells you to enter the cash flow for time 0. Since you need to send cash out of the company to make the initial $100 investment, this value has to be negative. Type in -100 for CF0, and hit the [ENTER] key.

Step 2: Entering the Cash Inflows

Next, enter the cash flow values for the subsequent periods. This is done by hitting the down arrow once. The calculator should read CF1=. Type in the first cash flow amount, 20, and hit [ENTER]. The calculator should now say C01=20.

To enter cash flow from Year 2, hit the down arrow twice. The calculator should read CF2=. If it says F1=, hit the down arrow one more time.

Type in the second year’s cash flow, 20, and hit [Enter]. The calculator should read CF2=20. Hit the down arrow twice again and do the same thing for the third cash flow period, CF3.

Do this once more and enter the last cash flow for the last time, 33.

Step 3: Calculating the IRR

Once the cash flow values have been fed into the calculator, you can calculate the IRR.

To do this, press the [IRR] key. The screen will read IRR=0.000. To display the IRR value for the data set, press the [CPT] key at the top left corner of the calculator. If you have followed this process correctly, the calculator will display the correct IRR. The IRR is computed to be -2.626%. Since \(-2.626\% \lt 8\%\), the project should not be undertaken.

Simply computing a project’s NPV and IRR to determine which of several projects to undertake is not always as straightforward as it seems. The IRR and NPV can produce different ranking outcomes whenever mutually exclusive projects are involved. Other challenges may occur.

Graphical Illustration

The NPV Profile illustrates a project’s NPV graphed as a function of various discount rates. The NPV values are graphed on the vertical or y-axis, while the discount rates are graphed on the horizontal or x-axis.

• The graph crosses the y-axis (vertical axis) when the discount rate = 0%; and
• The graph crosses the x-axis (horizontal axis) when the NPV = 0 and the discount rate is the IRR.

NPV and IRR Comparison

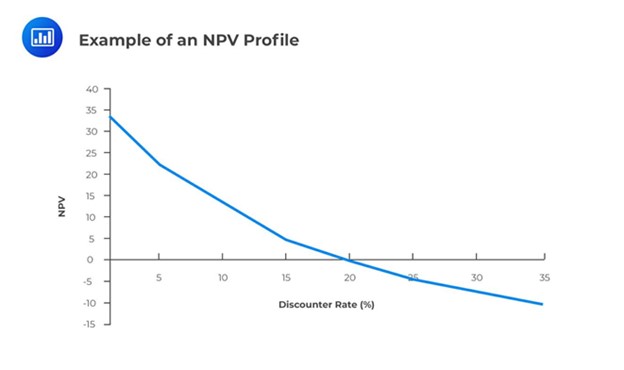
For independent, conventional projects, the NPV and IRR decision rules will draw the same conclusion on whether to invest. However, in the case of two mutually exclusive projects, sometimes the decision rules will draw different conclusions. For example, project X might have a more significant NPV than Project Y, but Project Y might have a larger IRR. This conflict usually stems from differences in the cash flows of the two projects, which leads to a different ranking between the NPV and IRR. Whenever this conflict arises, the NPV, not the IRR, should be used to select which project to invest in.

Another circumstance that may cause mutually exclusive projects to be ranked differently according to NPV and IRR criteria is the scale or size of the project.

Multiple IRR and No IRR Problem

Although rare, a project can have more than one IRR or no IRR at all. Multiple IRRs, however, cannot occur for conventional projects with outlay followed by cash inflows. Still, they may occur for non-conventional projects with cash flows that change signs (negative, positive) more than once during the project’s life.

The net present value (NPV) and the internal rate of return (IRR) are both techniques that can be used by financial institutions or individuals when making major investment decisions. Each method has its strengths and weaknesses. However, the net present value method comes out on top, and here’s why. NPV and IRR yield the same investment decisions when dealing with independent projects. By independent, we mean that deciding to invest in one project does not rule out or affect investment in the other project.

However, the challenge comes when the projects are mutually exclusive. If two or more projects are mutually exclusive, the decision to invest in one project precludes investment in all the others. With such projects, the IRR method may provide misleading results if used in isolation.

Shortcomings of IRR

As seen, there are some problems associated with the IRR method:

• The method assumes that all proceeds from a project are immediately reinvested in projects offering a rate of return equal to the IRR – this is very difficult in practice.
• It gives different rankings when the projects under comparison have different scales.
• Sometimes, the method may not provide a unique solution, especially when a project has a mixture of positive and negative cash flows during its productive life.

Return on Invested Capital

Return on capital invested (ROIC), also known as return on capital employed (ROCE), is a measure of profitability for total capital invested by management.

The formula is as follows.

$$ \begin{align*}
ROIC & =\frac{{\text{After-tax operating profit}}_t}{\text{Average invested capital}} \\ & =\frac{\left(1-\text{Tax rate}\right)\times{\text{Operating profit}}_t}{{\text{Average total Long Term liabilities and equity}}_{t-1,l}}
\end{align*} $$

Working capital is not included in the total capital investment. Invested capital includes long-term liabilities and equity.

Benefits of ROIC

• It can be calculated by independent investment analysts because the data is readily available, unlike IRR and NPV.
• ROIC considers the amount of capital the company needs to generate returns, unlike other profitability measures such as operating profit margin.

The link between ROIC is as follows:

$$ \begin{align*}
ROIC & =\frac{\text{After-tax operating profit}_t}{\text{Average invested capital}} \\ & =\frac{{\text{After-tax operating profit}}_t}{\text{Sales}}\times\frac{\text{Sales}}{\text{Average invested capital}} \\ &=\text{After-tax operating margin}\times \text{Capital turnover} \end{align*} $$

Therefore, two factors that influence ROIC are profit margin and turnover. This implies that a company with a high margin can have a low ROIC if the turnover is low and vice versa.

Example: Calculating ROIC

Consider the following excerpt of the balance sheet information of a company:

$$ \begin{array}{l|r|r}
\textbf{Liabilities and Equity} & \bf{20X1} & \bf{20X2} \\ \hline
\text{Accounts payable} & 37,500 & 52,800 \\ \hline
\text{Short-term debt} & 22,000 & 6,500 \\ \hline
\text{Long-term debt} & 113,000 & 107,500 \\ \hline
\text{Share capital} & 16,000 & 16,000 \\ \hline
\text{Retained earnings} & 150,000 & 162,500 \\ \hline
\text{Total liabilities and equity} & 338,500 & 345,300
\end{array} $$

If the company reported an operating profit in year 20X2 of 30,500, the ROIC for the year 20X2 if the tax rate is 30% is closest to:

$$ \begin{align*}
ROIC & =\frac{{\text{After-tax operating profit}}_t}{\text{Average invested capital}} \\ & =\frac{\left(1-\text{Tax rate}\right)\times{\text{Operating profit}}_t}{{\text{Average total Long Term liabilities and equity}}_{t-1,l}}
\\& =\frac{\left(1-0.3\right)\times30,500}{\frac{(113,000+16,000+150,000)+(107,000+16,000+162,000)}{2}}=0.07570\approx7.60\% \end{align*} $$

Comparison between ROIC, IRR, and NPV

• Unlike IRR and NPV, ROIC allows analysts to measure the firm’s ability to create value across all investments, not just individual projects. This is important because only the company can invest in individual project and not the investors.
• ROIC can be compared to the required rate of return of the investors. If the ROIC of a corporate issuer is higher than the required rate of return, then the issuer is creating value for investors. On the other hand, if the investors’ required rate of return is less than an issuer’s ROIC over time, then it suggests that investors might have benefited more from investing in other opportunities.In such cases, the issuer should consider enhancing turnover or profit margins, divesting from underachieving sectors, redistributing capital, or exploring other investment opportunities with higher yields.
• ROIC can be compared to the required rate of return for both equity and debt investors because it measures the return that an issuer will earn by investing in both equity and debt.

Limitations of ROIC

• Unlike IRR and NPV, ROIC is an accounting measure and not a cash-based measure. Thus, cash flows and operating profit can be materially different because of differences between capital expenditures and depreciation and the recognition rules of certain items.
• ROIC is backward-looking and can vary from year to year, depending on investment activity and business conditions.
• Due to its high aggregation, ROIC can obscure unprofitable or profitable areas of the issuer.

Question 1

You have been provided with the following cash flows for a capital project:

$$ \begin{array}{c|c|c|c|c|c|c}
\text{Year} & 0 & 1 & 2 & 3 & 4 & 5 \\ \hline
{\text{Cash flow } (\$)} & -50,000 & 10,000 & 10,000 & 15,000 & 15,000 & 15,000
\end{array} $$

Given a required rate of return of 8 percent, the NPV and IRR of the project are closest to:

1. NPV: $1,023; IRR: 10.64%.
2. NPV: $974; IRR: 8.68%.
3. NPV: $2,400; IRR: 7.12%.

Solution

The correct answer is B.

$$ \begin{align*}
NPV &=-50,000+\frac{10,000}{{1.08}^1}+\frac{10,000}{{1.08}^2}+\frac{15,000}{{1.08}^3}+\frac{15,000}{{1.08}^4}+\frac{15,000}{{1.08}^5} \\
NPV & =-50,000+9259.26+8573.39+11,907.48++11,025.45 \\ & +10,208.75 \\ &=\$974.33 \text{ million}
\end{align*} $$

Question 2

In an NPV profile, the point at which the profile crosses the x-axis is best described as:

1. The project’s IRR.
2. The point at which the NPV is highest.
3. The point at which the discount rate = 0% and the NPV is the sum of the undiscounted cash flows for the project.

Solution

The correct answer is A.

At the horizontal axis, the NPV = 0, and by definition, this occurs whenever the discount rate is the IRR.

Question 3

Suppose you have three independent projects – X, Y, and Z. Assume the hurdle rate is 12% for all three projects. Their NPVs and IRRs are shown below.

$$ \begin{array}{c|c|c|c}
& \text{Project X} & \text{Project Y} & \text{Project Z} \\ \hline
\text{NPV} & \$20,000 & \$21,400 & \$23,000 \\ \hline
\text{IRR} & 20\% & 32\% & 18\%
\end{array} $$

Assuming the projects are mutually exclusive, which of the following is the most economically feasible project?

1. Z
2. X
3. Y

Solution

The correct answer is A.

$$ \begin{array}{c|c|c|c}
& \text{Project X} & \text{Project Y} & \text{Project Z} \\ \hline
\text{NPV} & \$20,000 & \$21,400 & \$23,000 \\ \hline
\text{IRR} & 20\% & 32\% & 18\% \\ \hline
\text{Decision} & \text{Accept} & \text{Accept} & \text{Accept}
\end{array} $$

If the IRR criteria is used, all three projects would be accepted because they would all increase shareholders’ wealth. Their NPVs are all positive, and the three are all acceptable.

However, only one would be chosen if the projects are mutually exclusive. If one were to pick one project based on internal rates of return of the projects, one would go for Y. This is because its IRR is the highest compared to the other projects.

This decision would be wrong when we consider the sizes of the NPVs of the projects. While Y has the highest IRR, its NPV is lower than Z’s. The best decision would be to go for the project with the highest NPV, and that is project Z. Therefore, if projects are mutually exclusive, the NPV method should be applied.