Covariance and Correlation

Covariance

Covariance is a measure of how two variables move together. The sample covariance of X and Y is calculated as follows:

$${s}_{XY}=\frac{\sum_{i=1}^{N}\left(X_i-\bar{X}\right)\left(Y_i-\bar{Y}\right)}{n-1}$$

The formula above implies that the sample covariance is the mean of the product of the deviations in the two random variables and from their sample means.

If the covariance between two random variables is positive, it means they move in the same direction. When one is below its mean, the other is also below its mean, and vice versa.

A major drawback of covariance is that it is difficult to interpret since its value can vary from negative infinity to positive infinity.

Correlation

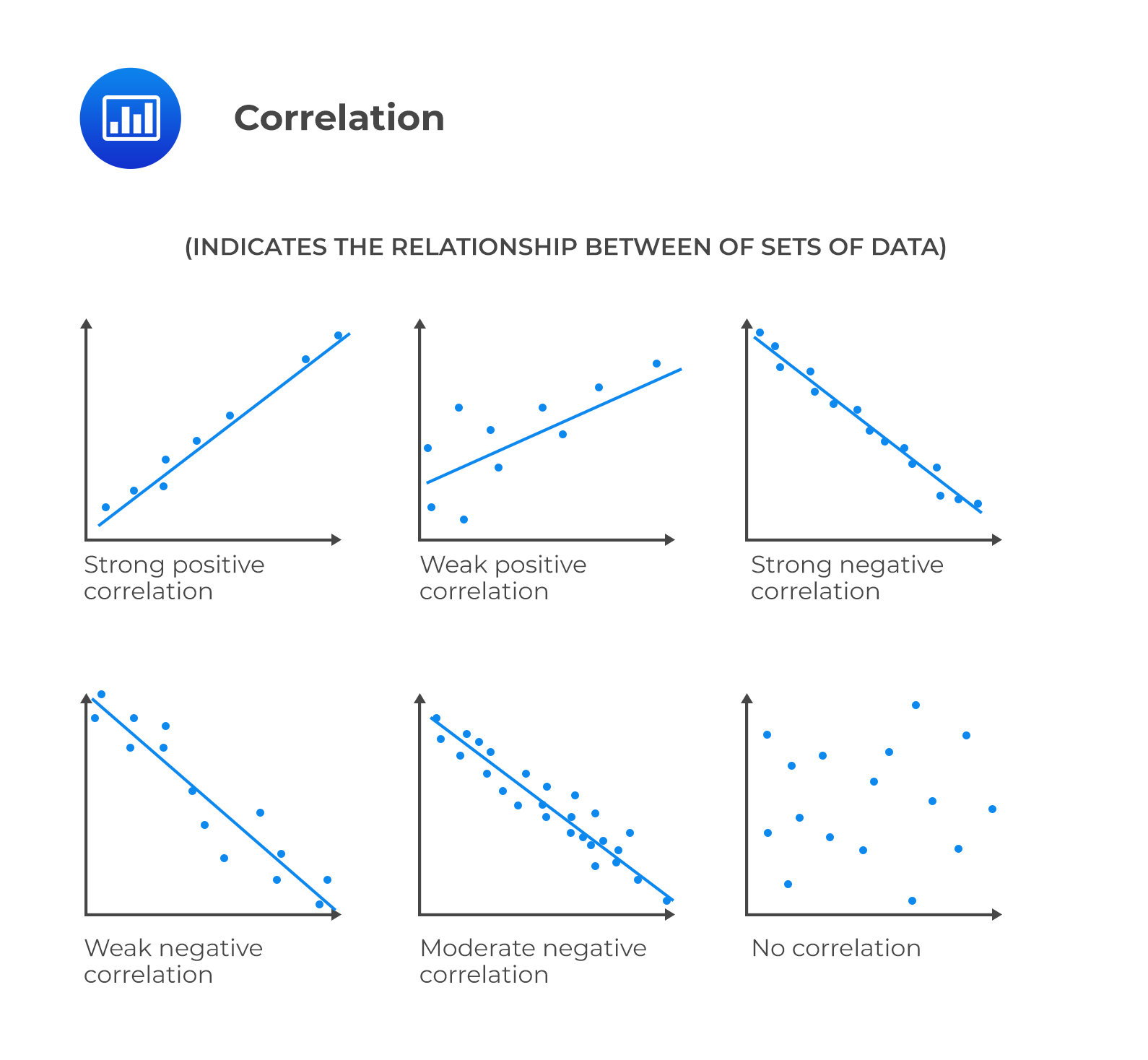
Correlation is a standardized measure of the linear relationship between two variables. It takes the covariance and divides it by the product of the standard deviations of both variables. As a result, its value ranges between -1 and +1 and is easier to interpret.

The sample correlation coefficient is calculated as follows:

$$r_{xy}=\frac{s_{XY}}{s_X\times s_Y}$$

Where:

\(s_{X Y}\) = Covariance between variable X and Y.

\(s_{X}\) = Standard deviation of variable X.

\(s_{Y}\) = Standard deviation of variable Y.

Properties of Correlation

• Correlation ranges between -1 to +1 for two random variables, X and Y.
• A correlation of 0 (uncorrelated variables) indicates that no linear (straight-line) relationship exists between the variables.
• A positive correlation close to +1 indicates a strong positive linear relationship.
  • A correlation of 1 indicates a perfect linear relationship.
• A negative correlation close to -1 indicates a strong negative linear relationship.
  • A correlation of -1 indicates a perfect inverse linear relationship.

Limitations of Correlation Analysis

• Two variables can have a very low correlation despite having a strong nonlinear relationship.
• Correlation can be an unreliable measure when outliers are present in the data.
• Correlation does not imply causation. This implies that the correlation may be spurious. A spurious correlation refers to:
  • Correlation between two variables due to chance relationships in a particular dataset.
  • Correlation arising between variables when they are divided by a third variable.
  • Correlation between two variables arising from their relation to a third variable.

Question

The correlation coefficient between X and Y is 0.7, and the covariance is 29. If the variance of Y is 25, the variance of X is closest to:

1. 8.29.
2. 29.00
3. 68.65.

Solution

The correct answer is C.

$$\begin{align} r_{X Y} &=\frac{s_{X Y}}{s_{X} \times s_{Y}}\\ \Rightarrow 0.7 &=\frac{29}{s_{X} \times 5} \\ \therefore s_{X}&=8.2857\\ \\ \text{Variance} &=8.2857^2=68.65 \end{align}$$