Using the Standard Normal Distribution to Calculate Probabilities

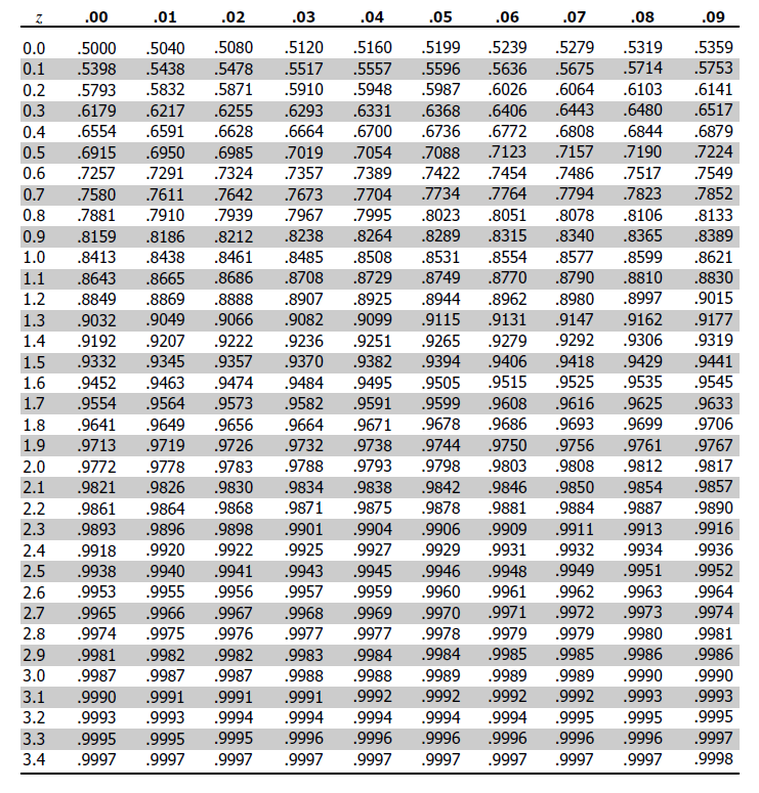
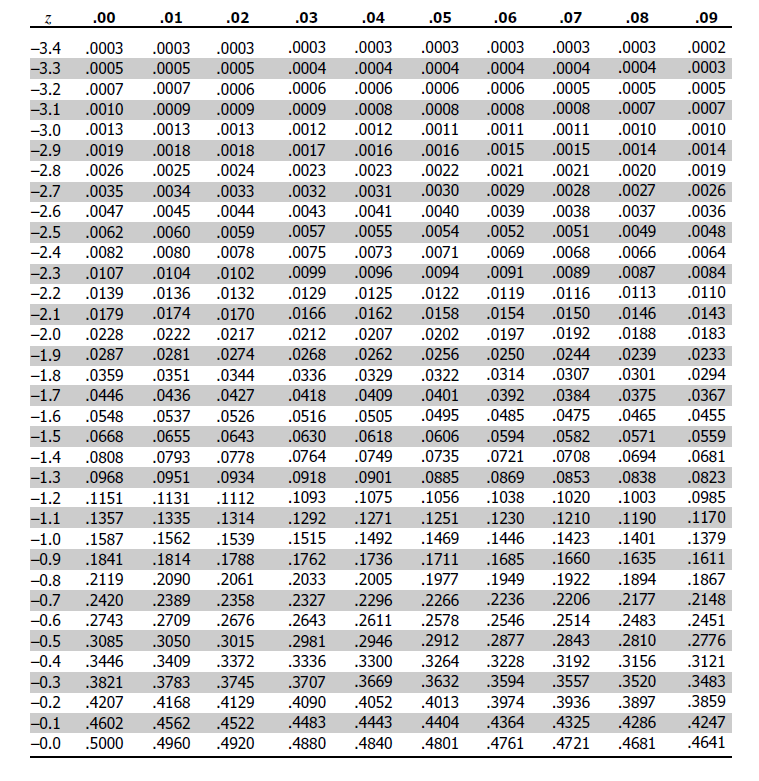
Using the standard normal distribution table, we can confirm that a normally distributed random variable \(Z\), with a mean equal to 0 and variance equal to 1, is less than or equal to \(z\), i.e., \(P(Z ≤ z)\).

However, the table does this only when we have positive values of \(z\). Simply put, if an examiner asks you to find the probability behind a given positive z-value, you will have to look it up directly on the table, knowing that \(P(Z ≤ z) = θ(z)\) when \(z\) is positive.

Positive z-values

Example: Using the z-score Table

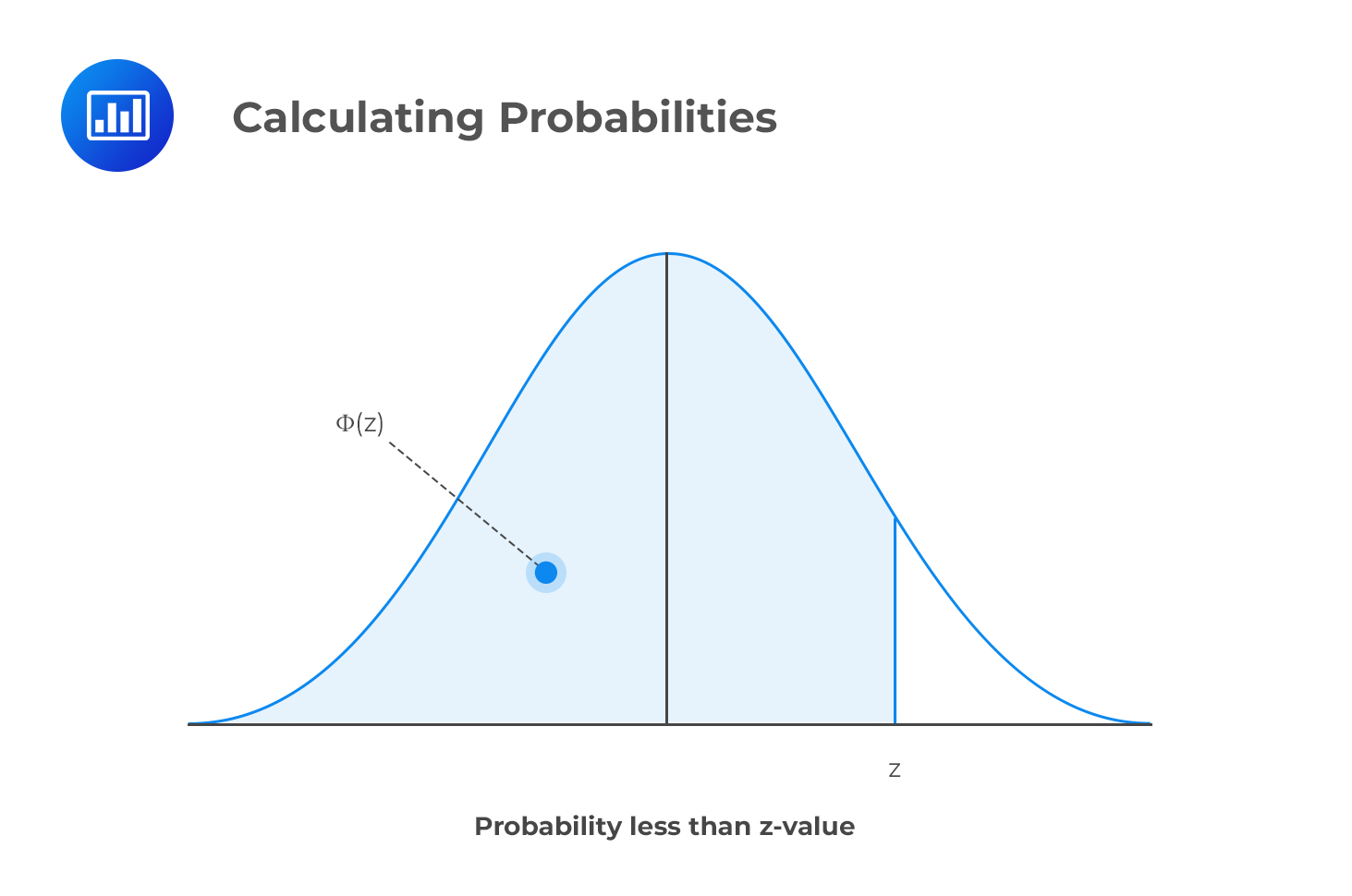
The returns on ABC stock are normally distributed, where the mean is $0.60 with a standard deviation of $0.20. The probability that the return is less than $1 is closest to:

Solution

If the return is $0.10, then \(x = 0.1\) (this is our observed value). Therefore,

$$\begin{align} z &=\frac{x-\mu}{\sigma}\\&=\frac{1-0.6}{0.2}\\ &=2\ \text{(The return of \$1 is two and a half standard deviations below the mean)}\end{align}$$

First, you’d be required to calculate the z-value (2 in this case). \(P(Z ≤ 1)\) can be read directly from the table

You just move down and locate the z-value that lies to the right of “2,” i.e., 0.9772.

Negative z-values

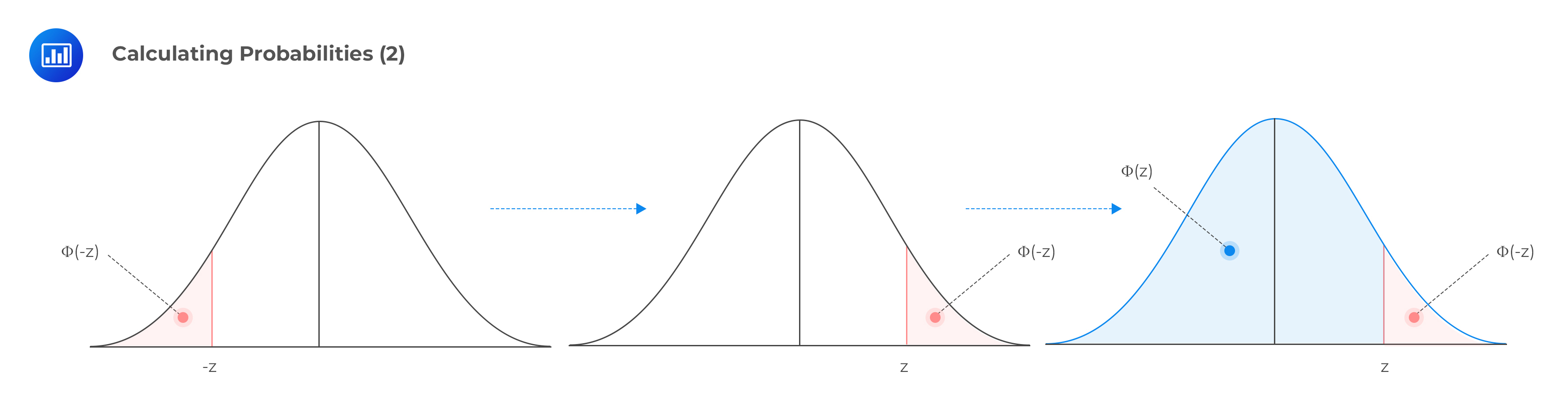
If we have a negative z-value and do not have access to the negative values from the table (as shown below), we can still calculate the corresponding probability by noting that:

$$ \begin{align} P(Z  \le -z) & = 1 – P(Z \le z) \\  \theta(–z) & = 1 – \theta(z) \\ 0.0228 & = 1 – 0.9772 \end{align}$$

This relationship is true when we consider the following facts:

1. The total area (probability) under the standard normal distribution is 1.
2. The standardized normal distribution is symmetrical about the mean.

Question

Calculate P(Z  ≤ -2.5).

A. 0.9938.

B. 0.0062.

C. 0.06.

Solution

The correct answer is B.

$$ \begin{align*} P(Z  \le -2.5) & = 1 – P(Z  \le 2.5) \\ & = 1 – 0.9938 \\ & = 0.0062 \\ \end{align*} $$