Shortfall Risk, Safety-first Ratio, and Identification of an Optimal Portfolio Using Roy’s Safety-first Criterion

Shortfall risk refers to the probability that a portfolio will not exceed the minimum (benchmark) return that an investor has set. In other words, it is the risk that a portfolio will fall short of the level of return an investor considers acceptable. As such, shortfall risks are downside risks. While a shortfall risk focuses on the downside economic risk, the standard deviation measures the overall volatility of a financial asset.

Safety-first Ratio

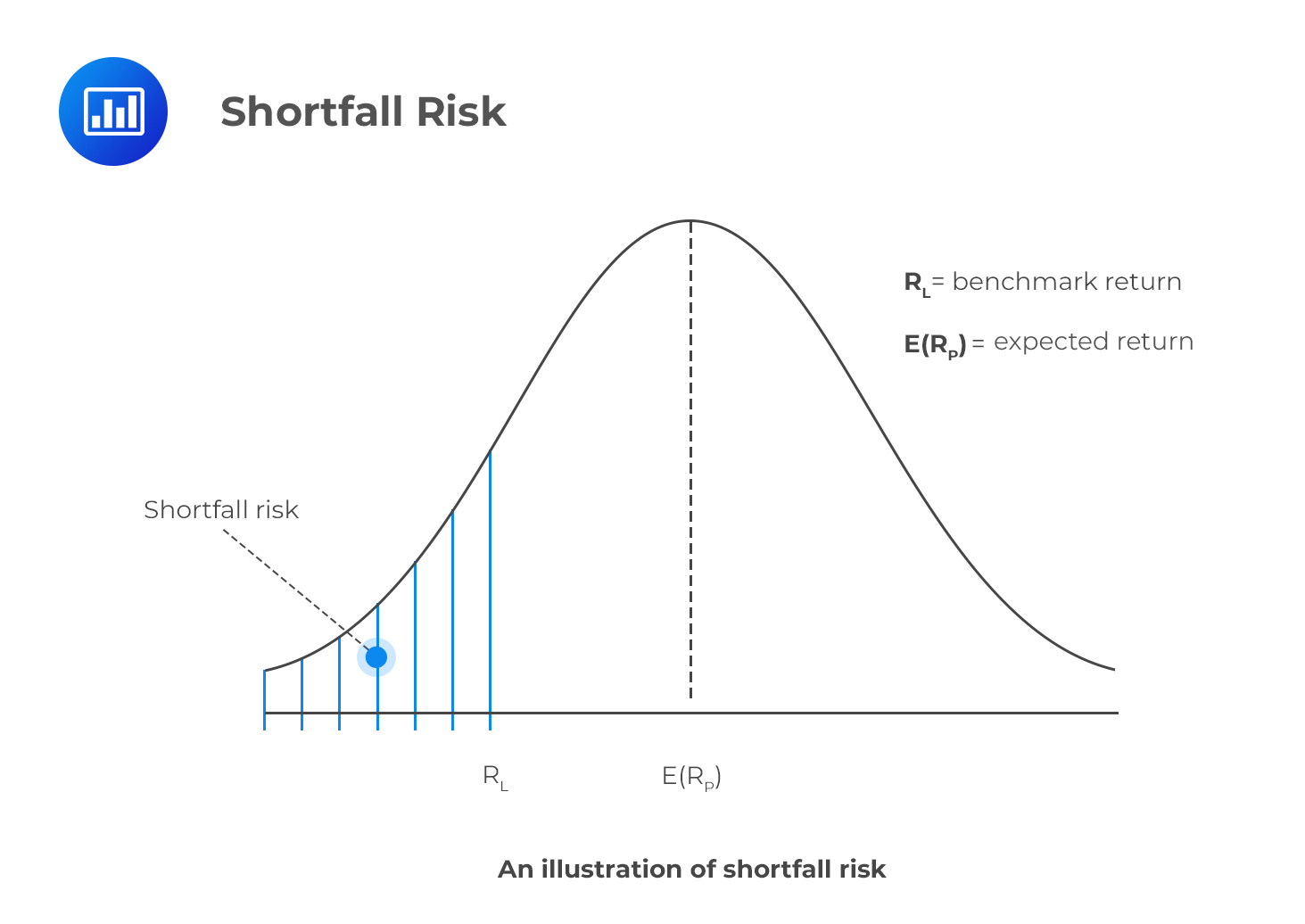
Roy’s safety-first criterion states that the optimal portfolio is the one that minimizes the probability that a portfolio return, denoted by \(R_P\), may fall below the threshold level of return, \(R_L\). The optimal portfolio minimizes \(P(R_P < R_L)\).

As such, if returns are distributed normally, the optimal portfolio is the one with the highest safety-first ratio.

$$ \text{SFRatio}=\frac { E\left( { R }_{ p } \right) -{ R }_{ L } }{ \sigma _{ p } } $$

The numerator, \(E(R_P)\) – \(R_L\), represents the distance from the mean return to the threshold level, i.e., it measures the excess return over and above the threshold level of return per unit risk.

Example: Safety-first Ratio

An investor sets a minimum threshold of 3%. There are three portfolios from which he is to choose one. The expected return and the standard deviation for each portfolio are as given below:

$$ \begin{array}{c|c|c|c} {} & \textbf{Portfolio A} & \textbf{Portfolio B} & \textbf{Portfolio C} \\ \hline {\text {Expected return}} & {5\%} & {10\%} & {20\%} \\ \hline \text{Standard deviation} & {15\%} & {20\%} & {25\%} \\ \end{array} $$

What is the optimal portfolio for the investor?

Solution

You should compute the safety-first ratio for each of the three portfolios and then compare them.

For portfolio A:

$$ \text{SFRatio}_{\text A} =\cfrac {(5 – 3)}{15} = 0.1333 $$

Similarly, for portfolio B:

$$ \text{SFRatio}_{\text B} =\cfrac {(10 – 3)}{20} = 0.35 $$

Lastly:

$$ \text{SFRatio}_{\text C}=\cfrac {(20 – 3)}{25} = 0.68 $$

The optimal portfolio should minimize the safety-first ratio. Comparing the three ratios, it is easy to notice that the safety-first ratio for portfolio C is the highest. Therefore, the investor should choose portfolio C.

Question

The returns on a fund are distributed normally. At the end of year \(t\), the fund has a value of $100,000. At the end of year \(t+1\), the fund manager wishes to withdraw $10,000 for further funding, but is reluctant to tap into the $100,000 dollars. There are two investment options:

$$ \begin{array}{c|c|c} {} & \text{Portfolio A} & \text {Portfolio B} \\ \hline {\text{Expected return} } & {14\%} & {13\%} \\ \hline \text{Standard deviation} & {17\%} & {20\%} \\ \end{array} $$

Which portfolio is preferable for the manager?

A. Portfolio A.

B. Portfolio B.

C. The manager is indifferent to the two portfolios.

Solution

The correct answer is A.

First, you should calculate the threshold return from the information given. Since there should be no tapping into the fund, the threshold return is \(\cfrac {10,000}{100,000} = 10\% \text { or } 0.1\).

You should then calculate the safety-first ratio for each portfolio:

$$ \text{SFRatio}_{\text A} =\cfrac {(14 – 10)}{17} = 0.24 $$

$$ \text{SFRatio}_{\text B} =\cfrac {(13 – 10)}{20} = 0.15 $$

Portfolio A has the highest safety-first ratio. This is the reason it is the most desirable.

Note to candidates: You can also go a step further and calculate \(P(R_P < R_L)\). To do this, you would have to negate each safety-first ratio and then find the CDF of the standard normal distribution for the resulting value. That is,

$$ \begin{align*}
P(R_P < R_L) & = F(-\text{SFRatio}) \\
F(-0.24)& = 1 – 0.5948 = 0.4052 \\
F(-0.15) & = 1 – 0.5596 = 0.4404 \\
\end{align*} $$

$$ (-\text{Where SFRatio is the z-value}) $$

Interpretation: For portfolio A, there is approximately a 40% probability of obtaining a return below the threshold return. For portfolio B, this probability rises to 44%. Therefore, we choose the option for which the chance of not exceeding the benchmark return is lowest – portfolio A.