Resampling

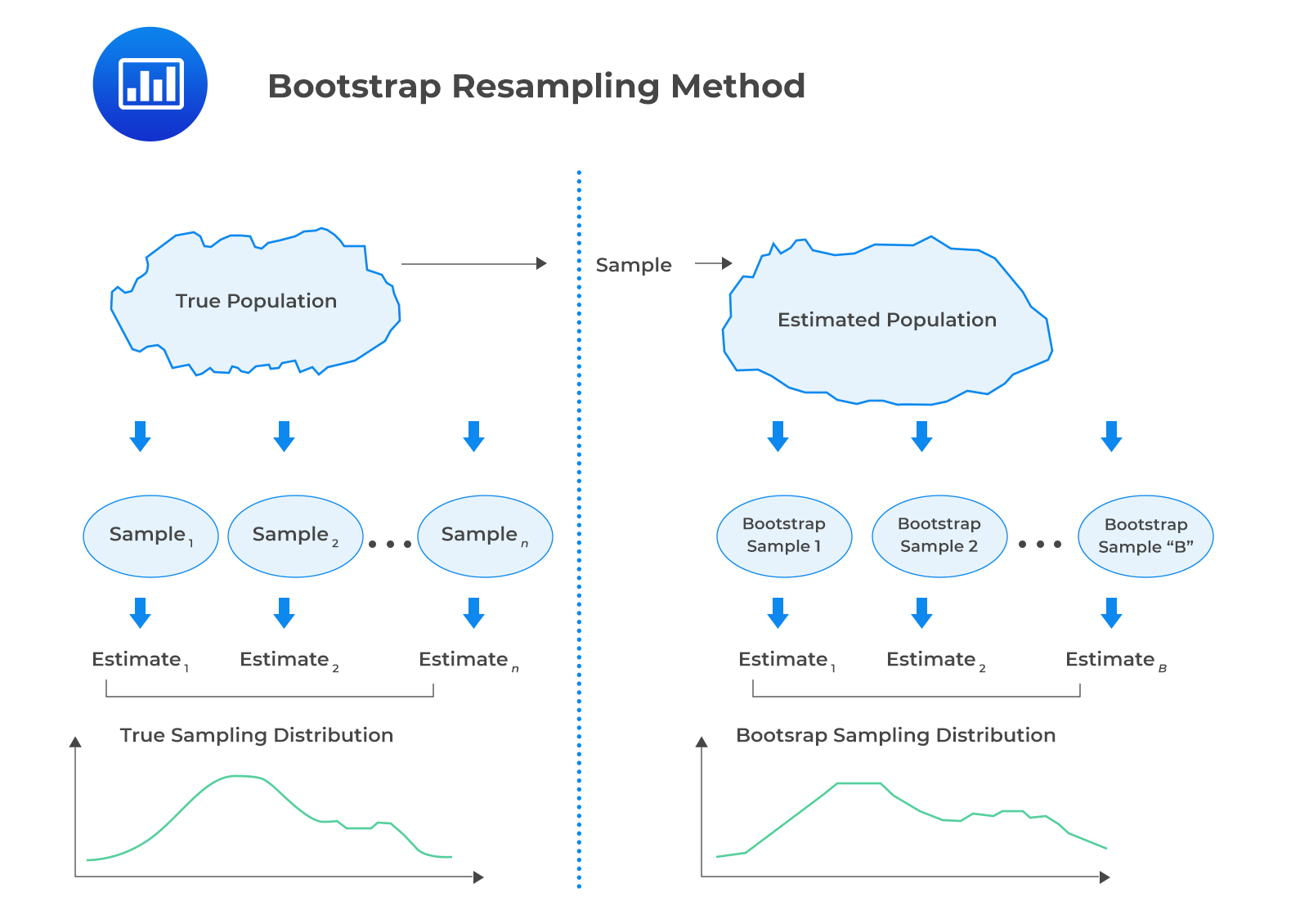
Resampling refers to the act of repeatedly drawing samples from the original observed data sample for the statistical inference of population parameters. The following are the two commonly used methods of resampling: Bootstrap and jackknife.

Bootstrap

In the bootstrap resampling method, a computer simulation is used to repeatedly draw random samples from the original sample. The resamples are then used to construct a sampling distribution.

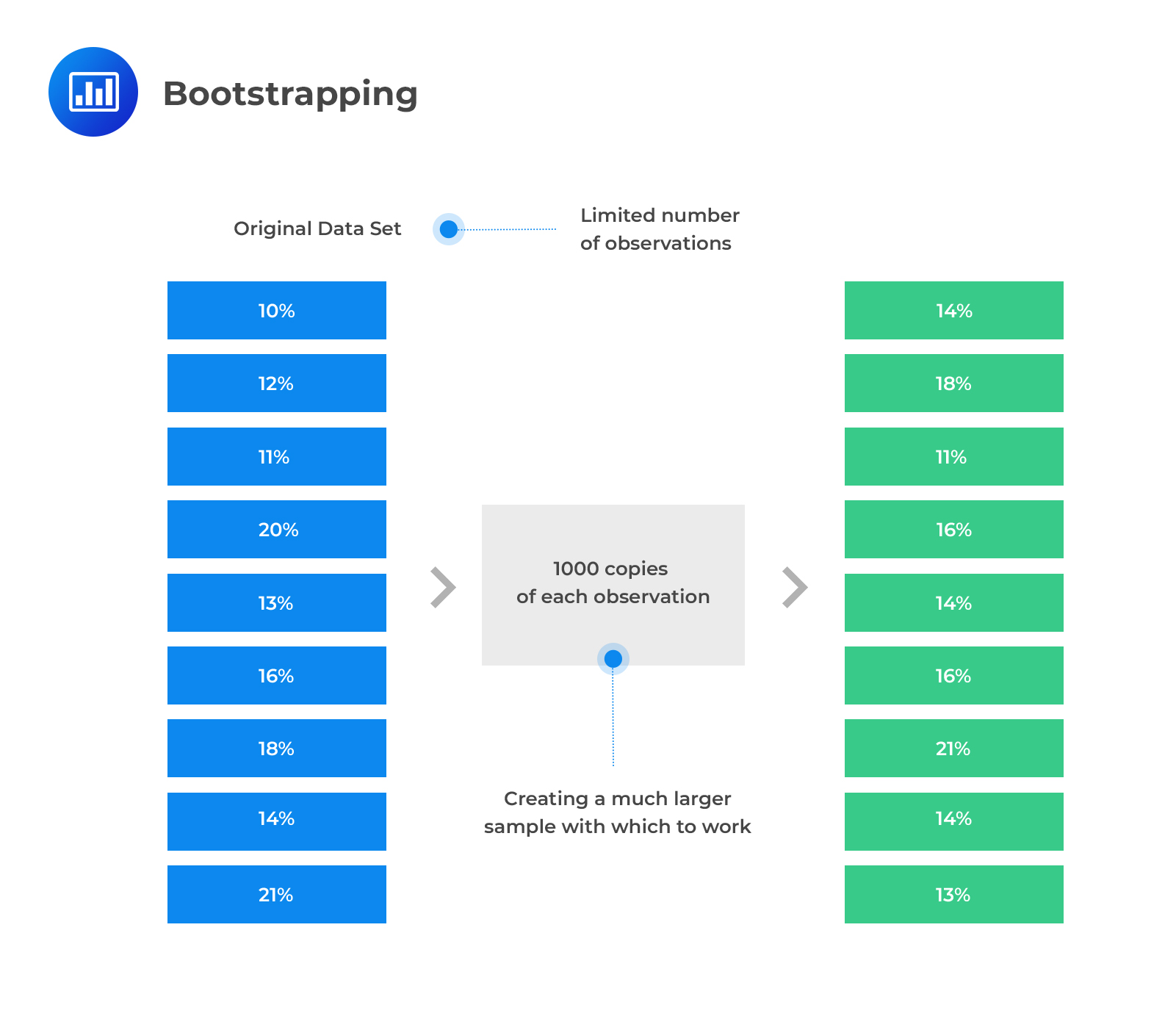
In the bootstrap method, the number of repeated samples to be drawn is at the discretion of the researcher. Furthermore, we can calculate the standard error of the mean. This is done by resampling and calculating the mean of each sample. The following formula is used to estimate the standard error.

$$ s_{\bar{X}}=\sqrt{\frac{1}{B-1} \sum_{b=1}^{B}\left(\hat{\theta}_{b}-\bar{\theta}\right)^{2}} $$

Where:

\(s_{\bar{X}}\) = Estimate of the standard error of the sample mean.

\(B\) = Number of resamples drawn from the original sample.

\(\hat{\theta}_{b}\) = Mean of a resample.

\(\bar{\theta}\) = Mean across all the resample means.

The bootstrap resampling method can also be used in the estimation of the confidence intervals for the statistic. Alternatively, it can be used to find other population parameters.  

Jackknife

Jackknife is a resampling method in which samples are selected by taking the original observed data sample and leaving out one observation at a time. As such, the samples are drawn without replacement. For a sample size of n, we need n repeated samples. This method can be used to reduce the bias of an estimator or to estimate the standard error and the confidence interval of an estimator.

Question

Assume that you are studying the median height of 100 students in a university. You draw a sample of 1000 students and obtain 1000 median heights. The mean across all resample means is 5.8. The sum of squares of the differences between each sample mean and the mean across all resample means \(\left(\sum_{b=1}^{B}{\left(\hat{\theta}_{b}-\bar{\theta}\right)^{2}}\right)\) is 2.3.

The estimate of the standard error of the sample mean is closest to:

1. 0.05.
2. 0.08.
3. 0.10.

Solution

The correct answer is A.

$$
\begin{aligned}
S_{\bar{X}}&=\sqrt{\frac{1}{B-1}} \sum_{b=1}^{B}\left(\hat{\theta}_{b}-\bar{\theta}\right) ^ 2 \\
&=\sqrt{\frac{1}{1000-1}}(2.3)=0.04798
\end{aligned}
$$