Liquidity and Leverage

>

After completing this reading, you should be able to:

• Differentiate between sources of liquidity risk and describe specific challenges faced by different types of financial institutions in managing liquidity risk.
• Summarize the asset-liability management process at a fractional reserve bank, including the process of liquidity transformation.
• Compare transactions used in the collateral market and explain risks that can arise through collateral market transactions.
• Describe the relationship between leverage and a firm’s return profile (including the leverage effect) and distinguish the impact of different types of transactions on a firm’s leverage and balance sheet.
• Distinguish methods to measure and manage funding liquidity risk and transactions liquidity risk.
• Calculate the expected transaction cost and the spread risk factor for a transaction and calculate the liquidity adjustment to VaR for a position to be liquidated over a number of trading days.
• Discuss interactions between different types of liquidity risk and explain how liquidity risk events can increase systemic risk.

Sources of Liquidity Risk and How Each of the Risks Arises for Financial Institutions

In financial markets, an asset is liquid if it is a good substitute for cash. In other words, the asset can be converted into cash quickly at a reasonable price without fluctuating the price significantly. A market is liquid if market participants unwind positions rapidly, at reasonable transaction costs, and without excessive price deterioration.

Liquidity has two major categories: transaction liquidity and funding liquidity. Transaction liquidity takes financial assets and financial markets into consideration. It is the ability to buy or sell an asset without moving its price. On the other hand, funding liquidity relates to an individual’s or an organization’s creditworthiness. It is the ability to finance assets continuously at an acceptable borrowing rate.

There are different risks related to liquidity which include:

Transaction liquidity risk: This is the risk that results in the adverse price movement of an asset during buy and sell transactions. Transaction liquidity risk is low if assets can be liquidated quickly and cheaply, without moving the price “too much to exchange an asset for other assets easily.”

Balance sheet risk (funding liquidity risk): Funding liquidity risk occurs when lenders withdraw or change the terms of borrowing due to the deteriorating credit position of the borrower. Typically, in the banking sector, funding liquidity risk is high due to maturity mismatch, i.e., funding long-term assets (bank loans) with short-term liabilities (bank deposits).

A maturity mismatch is often profitable for a short-term borrower. This is because of the lower cost of capital owing to less risk of borrowing and a decreased required rate of return. The profit is even more in the case of an upward-sloping yield curve. However, maturity mismatch exposes the borrower to rollover risk. Also called cliff risk, it is associated with the refinancing of debt at higher interest rates.

Systemic risk: This is the risk of failure of the entire financial system due to heavy financial stress.

Different types of liquidity risks are correlated, and this accelerates problems. For example, if the counterparty increases collateral requirements, the investor may have to unwind it before the full realization of the expected return. Reducing the trade horizon causes deterioration of funding liquidity, which increases the transaction liquidity risk.

Asset-liability Management Process at a Fractional Reserve Bank and Liquidity Transformation

A commercial bank’s core function is to take deposits and to provide loans to non-financial institutions. It transforms long-term illiquid assets (loans) into short-term liquid ones (deposits). This enables the banks to carry out liquidity, credit, and maturity transformation. Banks also raise funds by issuing bonds, commercial paper, and other forms of debt. This is called wholesale funding, and it involves longer-term deposits, which can be redeemed at short notice. Bank deposits are “sticky.” Depositors remain in the bank unless impelled to change banks’ circumstances such as moving houses.

Bank assets are typically long term and less liquid (Loans). On the other hand, bank deposits that contribute to roughly 60-70% of the bank’s liabilities are short term, sticky, and more liquid. Banks use deposits for lending purposes. In other words, banks match short-term liabilities with long term assets. This is referred to the as fractional reserve banking system. A bank that lends deposits is known as a fractional-reserve bank. Banks also borrow (raise capital) from the external market through issuing bonds or commercial paper and use it for lending purposes. This is called wholesale funding and involves longer-term deposits.

A traditional asset-liability function of the bank is to ensure that it remains liquid by reducing funding liquidity risk. In other words, asset-liability management (ALM) is the process of using deposits to finance loans.

ALM is a crucial process which includes measures such as:

• Tracking and forecasting available cash and cash needs.
• Keeping specific ratios of cash and marketable securities to meet unusual demands by depositors.

However, so asset-liability management system can adequately protect a fractional-reserve bank against a loss of confidence in its ability to pay out depositors. No degree of liquidity can secure a bank entirely against a run as long as it executes a liquidity and maturity transformation, and has liabilities on-demand.

The following figure demonstrates the impact on a bank when its customers withdraw more than the bank’s reserves.

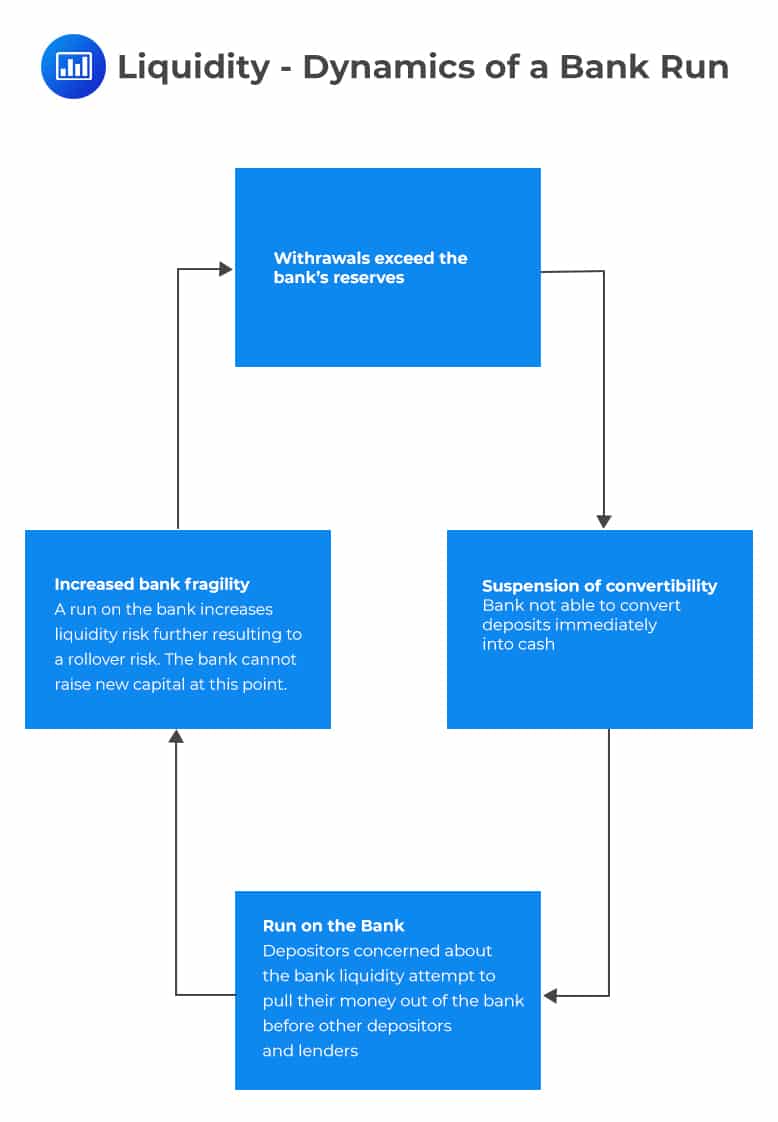A high fragility can be mitigated through higher capital. High capital reduces depositors’ concern about solvency, the typical trigger of a run, and higher reserves, which reduces concern about liquidity.

The fragility of bank funding was illustrated following the Lehman Brothers bankruptcy. Following the crisis, commercial paper borrowing abruptly declined as it could no longer be placed. Banks faced difficulty in rolling over the long-term commercial paper, and in obtaining funding with maturities of more than a few weeks. The share of very short-term issuance significantly increased to almost 90% due to fewer alternatives.

The Federal Reserve intervened after the Lehman bankruptcy and created the Commercial Paper Funding Facility (CPFF), which purchased the commercial paper from issuers unable to roll the paper over. It also purchased the Asset-Backed Commercial Paper Money Market Mutual Fund Liquidity Facility (AMLF), which lent to financial institutions purchasing ABCP from MMMFs.

Markets for Collateral and Risks Associated With Collateral Market Transactions

Markets for collateral are created when securities are used as collateral to obtain secured loans of cash or other securities. The borrower of securities can lend them to another, a practice called rehypothecation or repledging of collateral. Collateral is of the essence in credit transactions since it provides security for lenders, hence ensuring the availability of credit to borrowers. Besides, the use of collaterals makes it easy to establish short positions in securities.

A haircut is equivalent to the value of the collateral less the amount borrowed. From the lender’s perspective, the haircut is the extent to which collateral value can fall and still be fully collateralized. For example, suppose that an investor borrows $100. He invests a collateral of $102. The $2 difference is the one referred to as the haircut. The lender aims to ensure that the loan amount is less than the collateral.

Additionally, the lender may insist on the variation margin. This is a periodic additional fund deposit to maintain the difference between the lent amount and the collateral. The variation margin protects the lender against fluctuations in the value of the collateral. For example, if the haircut of $2 reduces to $1 at any particular period, the borrower must top up the amount by an additional $1 to maintain the haircut at $2.

The role of collateral has expanded in modern finance, following the progression of securitization. Securitization generates securities that can be pledged as collateral for credit. Securitized assets generate cash flows, may appreciate, and can be used as collateral for other transactions.

Collateral markets prop up the growth of non-bank intermediaries. Life insurance companies own portfolios of high-quality securities. This enables them to borrow cash at a low rate, which they can then invest in earning higher rates of return. Furthermore, hedge funds have inventories of securities that they use as collateral to get financing of the portfolio at a reduced rate than unsecured borrowing. Finally, Firms with excess cash are more willing to lend at a low rate of interest if the loan is secured by collateral.

Types of Collateral Markets

Margin loans: Margin loans are short-term financial securities that are collateralized with a broker in a street name account. In other words, the broker acts as an intermediary for the trade. He/she retains custody of the securities in a different customer account, a street account, (i.e., registered in the name of the broker rather than that of the owner). Registering using a street name account allows the broker to use the securities for other purposes. These may be borrowing money in the secured money market to obtain the funds he/she lends to margin customers as well as to meet margin calls.

Cross-margin agreements are used to put in place the net margin position of investors with portfolios of long and short positions. Cross margin involves transferring excess margin from one account to another account with an insufficient margin. This reduces the overall margin to the investor.

Repurchase Agreements (Repos): Repurchase agreements are a form of short-term collateralized loans sold to buy back at a later date at a higher price (the forward price). Both the spot and forward prices are agreed upon today, and the difference is the interest rate. Repos encompass high-yield bonds and whole loans, and more recently, structured credit products.

Securities Lending: Securities lending involves one party lending security to a counterparty at a fee, called a rebate. The lender continues to receive interest cash flows and dividends from the security. Stock lending involves the borrowing of stocks and it is a common type of securities lending.

Securities lending is generally carried out by hedge funds and other large institutional equity investors. The investor holds the equities through a broker in “street name,” thus making them available for lending. They can then be rehypothecated to a trader who wishes to sell the securities short. The investor receives a rebate in exchange. Fixed-income securities’ lending transaction aims to earn a spread between less and more risky bonds. For example, lending treasury securities and using the cash to invest in high-risk bonds.

Total Return Swaps: In a total return swap, a fixed payer earns the return (both income and capital gains) on a reference asset without owning it. The counterparty providing the return often a hedge fund establishes a short stock position, which is identical to that of a borrower of stock.

Leverage Ratio and Leverage Effect

The leverage is the ratio of the firm’s assets to its liabilities. The leverage ratio, also often called the debt-to-equity ratio, is given by:

$$ \text L=\cfrac {\text A}{\text E}=\cfrac {{\text E}+\text D}{\text E}=1+\cfrac {\text D}{\text E} $$

A leverage value of 1 implies that there is no debt. This is the lowest possible value of leverage. Leverage ratio increases with an increase in debt.

The leverage effect is the increase in the return on equity (ROE) that results from increasing leverage and is equivalent to the difference between the return on assets (ROA) and the cost of funding. The leverage effect can be expressed as:

$$ {\text r}^{\text e}=\text L{\text r}^{\text a }-(\text L-1) {\text r}^{\text d} $$

Where:

\({\text r}^{\text a }\)= Asset returns.

\({\text r}^{\text e }\)=Equity returns.

\({\text r}^{\text d }\)= Cost of debt.

\(\text L\) = Leverage ratio.

The above formula can also be expressed as:

$$ \text{ROE}=(\text{ROA}×\text{Leverage ratio})-[(\text{Leverage ratio}-1)×\text{cost of debt}] $$

The return on equity (ROE) increases with the increase in leverage as long as the return on assets (ROA) is greater than the cost of debt. Although the increase in leverage increases profits in good times, it can also magnify losses should the ROA prove to be lower than the cost of debt.

For example, if the leverage ratio is 4, 75% of the balance sheet is financed with debt, and only 25% is financed with equity. Therefore, for every $4 of assets, $3 is borrowed funds (debt), and $1 is equity. In the formula expression, we multiply the cost of debt by 3. The higher the leverage factor, the larger the multiplier but also the higher the debt costs. Leverage is also referred to as a double-edged sword because it amplifies gains but also magnifies losses.

The effect of increasing leverage is equivalent to the proportion of the change in retained earnings relative to the change in leverage. This can be expressed as:

$$ \cfrac {\partial {\text r}^{\text e }}{\partial {\text L}}={\text r}^{\text a }-{\text r}^{\text d } $$

Where:

\({\partial {\text r}^{\text e }}\)=Change in retained earnings.

\({\partial {\text L}}\)=Change in the leverage ratio.

This formula implies that increasing assets and taking on an equal amount of additional debt that increases leverage from an initial value \({\text L}_0\) to \(\text L_0\) +1 increases ROE by \({\text r}^{\text a }-{\text r}^{\text d }\).

The equity denominator of the leverage ratio depends on the type of entity and the purpose of the analysis. For example, for a bank, the equity might be the book value or market value of the firm. On the other hand, hedge funds use the net asset value (NAV) of the fund, which is the current value of the investor’s capital.

Example: Leverage and Leverage Effect

A firm has an ROA of \({\text r}^{\text a }=0.20\), while its cost of debt is \({\text r}^{\text d }=0.10\). The firm’s balance sheet is as given below:

$$ \begin{array}{l|c} \textbf{Assets} & \textbf{Value} \\ \hline \text{Value of the firm (V)} & {3} \\ \hline \text{ROA} & {0.2} \\ \hline \text{Liabilities} & {} \\ \hline {\text{Equity } € } & {1.5} \\ \hline \text{Debt (D)} & {1.5} \\ \hline \text{Leverage} & {2} \\ \hline {\text{Cost of debt} (\text r^{\text d})} & {0.1} \\ \hline \text{ROE} & {30\%} \\ \end{array} $$

Find the firm’s leverage and return on equity (ROE).

Solution

$$ \text{The firm’s leverage} = 1+\cfrac {\text D}{\text E}=1+\cfrac {1.5}{1.5}=2 $$

Its ROE is:

$$ \begin{align*} \text{ROE} & = (\text{ROA}×\text{Leverage ratio})-[(\text{Leverage ratio}-1)×\text{cost of debt}] \\ & =(0.2×2)-[(2-1)×0.10]=0.30 \text{ or } 30\% \\ \end{align*} $$

Example: Increasing the Amount of Debt

Using the previous example and increasing the leverage, by borrowing an extra unit of funds and investing it in an extra unit of assets, deviates the balance sheet to:

$$ \begin{array}{l|c} \textbf{Assets} & {} \\ \hline \text{Value of the firm (V)} & {4} \\ \hline \text{ROA} & {0.2} \\ \hline \textbf{Equity and Liabilities} & {} \\ \hline {\text{Equity } € } & {1.5} \\ \hline \text{Debt (D)} & {2.5} \\ \hline \text{Leverage} & {2.7} \\ \hline {\text{Cost of debt} (\text r^{\text d})} & {0.1} \\ \end{array} $$

Find the firm’s ROE.

Solution

$$ \text{The firm’s leverage} = 1+\cfrac {\text D}{\text E}=1+\cfrac {2.5}{1.5}=2.67 $$

$$ \begin{align*} \text{ROE} & = (\text{ROA}×\text{Leverage ratio})-[(\text{Leverage ratio}-1)×\text{cost of debt}] \\ & =(0.2×2.67)-[(2.67-1)×0.10]=0.37 \text{ or } 37\% \\ \end{align*} $$

As we can see, increasing the amount of debt increases the return on equity for shareholders in this instance.

Example: Hurdle Rate

The firm’s hurdle rate (i.e., required ROE) also influences the leverage. For example, assume a firm’s hurdle rate (i.e., ROE) is 12%, ROA equals 8%, and its cost of debt equals 4%. The firm chooses a leverage ratio of 2.0, as calculated below:

$$ \text{ROE} = (2 × 8\%) – (1 × 4\%) = 12\% $$

Explicit and Implicit Leverage

There exist two forms of leverage, explicit and implicit leverage. Explicit leverage occurs when performing margin purchases or issuing bonds to raise capital. This is because these tasks entail borrowing. For example, assume that a company’s balance sheet has equity of 50% and a debt capital of 50%. The securities are 100% The Company’s leverage ratio is:

$$ =1+\cfrac {50\%}{50\%}=2 $$

Therefore, explicit leverage is 2. Increasing the debt capital increases equity and thus increases the leverage ratio.

Implicit leverage refers to embedded leverage in short positions and derivatives such as options and swaps. Economic balance sheets can be used to measure implicit leverage.

Margin Loans and Leverage

First, we consider margin loans. The stock acquired with the margin loan is collateral for the loan. The haircut determines the amount of the loan made. At a haircut of h%, (1-h %) is loaned against a given market value of margin collateral, and h% is the borrower’s equity in the position. A position with a haircut of h% has a leverage of 1/h.

Example: Margin Loans and Leverage

Suppose that a firm has $200 in cash, following an investment of $200 in equity by its investors. If the firm uses all the cash to purchase stock, the balance sheet is:

$$ \begin{array}{l|c} \textbf{Assets} & \textbf{Value} \\ \hline \text{Cash} & {0} \\ \hline \text{Stock} & {200} \\ \hline \textbf{Total assets} & \bf{200} \\ \hline \textbf{Liabilities and Equity} & {} \\ \hline {\text{Equity } } & {200} \\ \hline \text{Debt (D)} & {0} \\ \hline \textbf{Total liabilities and equity} & \bf{200} \\ \hline \textbf{Leverage} & \bf{1} \\ \end{array} $$

$$ \text {The leverage ratio will be equal to:} 1+\cfrac {0}{200}=1 $$

Next, suppose that the firm uses 50% borrowed funds and invests 50% (i.e., h = 50%) equity in buying shares of stock. Immediately, the margin account balance sheet has 50% equity and a $50 margin loan from the broker.

The overall economic balance sheet as a result of the borrowed funds is:

$$ \begin{array}{l|c} \textbf{Assets} & \textbf{Value} \\ \hline \text{Cash} & {100} \\ \hline \text{Stock} & {100} \\ \hline \textbf{Total assets} & \bf{200} \\ \hline \textbf{Liabilities and Equity} & {} \\ \hline {\text{Equity } } & {200} \\ \hline \text{Margin Loan} & {100} \\ \hline \textbf{Total liabilities and equity} & \bf{300} \\ \hline \textbf{Leverage} & \bf{1.5} \\ \end{array} $$

Thus, the leverage ratio has risen to 1.5, i.e., \(1+\frac {100}{200}=1.5\). The broker retains control of the stock to use as collateral for the loan.

Short Positions and Leverage

Under a short sale, the investor borrows securities from the broker and sells them. Two transactions are involved here, one that involves borrowing and the one that involves selling. The transaction enlarges the balance sheet because the cash generated from the short sale along with the value of the borrowed securities appears on the balance sheet.

Example: Short Positions and Leverage

Assume a firm that has a hedge fund with $200 of cash, corresponding to $200 of equity invested by the owners. The firm then borrows $200 of stock and sells it short. It has assets equivalent to the proceeds from selling the stock and a liability equal to the value of the borrowed shares. However, the firm cannot use the cash for other investments because it is collateral. The broker uses the cash to ensure that the short stock can be repurchased and returned to the lender. It remains in a segregated short account. In case of an increase in the stock price, the firm must also put $100 in a margin account because the $200 of proceeds would not be enough to cover its returns to the borrower.

The immediate impact of this trade is that the firm’s margin and short accounts have $100 in equity and a $100 loan from the broker as follows:

$$ \begin{array}{l|c} \textbf{Assets} & \textbf{Value} \\ \hline \text{Due from the broker} & {300} \\ \hline \text{Margin} & {100} \\ \hline \text{Short sale proceeds} & {200} \\ \hline \textbf{Total assets} & \bf{300} \\ \hline \textbf{Liabilities and Equity} & {} \\ \hline {\text{Equity } } & {100} \\ \hline \text{Borrowed Stock} & {200} \\ \hline \textbf{Total liabilities and equity} & \bf{300} \\ \end{array} $$

The firm’s full economic balance sheet given the short sale is:

$$ \begin{array}{l|c} \textbf{Assets} & \textbf{Value} \\ \hline \text{Cash} & {100} \\ \hline \text{Due from the broker} & {300} \\ \hline \textbf{Total assets} & \bf{400} \\ \hline \textbf{Liabilities and Equity} & {} \\ \hline {\text{Equity } } & {200} \\ \hline \text{Borrowed Stock} & {200} \\ \hline \textbf{Total liabilities and equity} & \bf{400} \\ \hline \textbf{Leverage} & \bf{2} \\ \end{array} $$

The firm’s leverage has increased from 1 to 2, i.e.,1/0.50=2. The leverage is higher in this case than in the previous example of the long position. This is because the full value of the securities is borrowed in creating a short position. Leverage is intrinsic in the short position but is a choice in the long position. The firm only borrows half of the balance of the stock in the long position, making the leverage 1.5. On the contrary, the entire stock position must be borrowed to execute the short in this case.

Short positions reduce risk if there are long positions with which there is a positive correlation or other short positions with which they have a negative correlation. If the short position takes part in hedging a portfolio, the leverage overstates the overall risk since short positions increase leverage, but reduce market risk. This reduces the benefits of the short positions. This leads to a contrast between gross and net leverage. Gross leverage is the proportion of all the assets, including cash generated by short sales, divided by capital. On the other hand, net leverage is the ratio of the difference between the long and short positions by capital.

Derivatives and Leverage

Trading in derivatives involves exposure to an asset or a risk factor without buying or selling it outright. Since derivatives have a substantial impact on returns, they are included in the economic balance sheet by finding cash equivalent market value for each one of the derivatives.

Different types of derivatives have different uses and, therefore, have very different impacts on leverage. Futures, forwards, and swaps are linear and have symmetric underlying asset prices and can be hedged statically. They have a zero NPV at the initiation. Therefore, their cash-equivalent market value can be represented on an economic balance sheet by the market value of the underlying asset, instead of the NPV.

On the other hand, options have a nonlinear relationship to the underlying asset price and thus should be hedged dynamically. Contrary to futures, forwards, and swaps, options have a non-zero NPV at the initiation. This is because the value is decomposed into an intrinsic value, which is zero and a time value that is likely non-zero. The cash-equivalent market value of options can be represented on an economic balance sheet by their delta equivalents rather than their market values.

Example: Derivatives and Leverage

Suppose that a firm has a hedge fund account with $200 in cash, corresponding to an initial investment of $200 in equity by investors. The firm adds the following:

A long one-month euro-denominated bank deposit with an underlying index value of $200, financed by borrowing $200 for one month. Assume that the one-month forward exchange rate is $1.25 per euro. Note that $200 is equivalent to a $160 bank deposit.

An equity option, with a delta of 50%, which is equivalent to buying $50 worth of the S&P 500 index with a broker loan of $100:

A short equity position is expressed via a three-month equity total return swap (TRS). The firm pays the total return on the $200 market value of XYZ Ltd. Stocks and a short rebate or cost of borrowing XYZ Ltd. stock. If the market price of XYZ Ltd. is $200, we have:

$$ \begin{array}{l|c} \textbf{Assets} & \bf{\text {Amount} ($)} \\ \hline {\text{Amount due from broker}} & {200} \\ {\text{(proceeds from the short sale)}} & {} \\ \hline \text{Liabilities and Equity} \\ & {} \\ \hline \text{Borrowed XYZ stock} & {200} \\ \end{array} $$

Finally, short protection on XYZ Ltd. via a five year credit default swap (CDS). The notional amount of $200. This position is equal to a long position in a par-value 5-year floating rate note (FRN) financed with a term loan.

We assume that the counterparty is the same for all positions, i.e., the prime broker or broker-dealer with which they are executed. Assuming there is no margin, the firm’s combined economic balance sheet that includes all of the derivatives positions is:

$$ \begin{array}{l|c} \textbf{Assets} & \bf{\text{Amount} ($)} \\ \hline \text{Cash} & {100} \\ \hline \text{Amount due from broker} & {300} \\ \hline \text{margin} & {100} \\ \hline \text{Short sale proceeds} & {200} \\ \hline \text{Bank deposit (Euro 160)} & {200} \\ \hline \text{long S&P 500 position} & {100} \\ \hline \text{XYZ FRN} & {200} \\ \hline \textbf{Total Assets} & \bf{900} \\ \hline \textbf{Equity and Liabilities} & {} \\ \hline \text{Equity} & {200} \\ \hline \text{Short-term broker loan} & {300} \\ \hline \text{Term loan} & {200} \\ \hline \text{Borrowed stock} & {200} \\ \hline \textbf{Total equity and liabilities} & \bf{900} \\ \end{array} $$

From the above balance sheet, we can compute the leverage of the long positions of the fund as \(\frac {900}{200}=4.5\). Additionally, it has attained a short position with a magnitude equal to the NAV. It has thus acquired economic exposure to securities valued at $900, using only $100 in cash.

Computing leverage is sophisticated when derivatives are used. Also, correctly interpreting leverage is essential since the risk may be reduced if short positions are used to hedge. For example, interest rate risks can be hedged precisely. However, the positions are of the same magnitude as the underlying assets. If the positions are carried on the economic balance sheet, leverage will be overstated and other material risks in the portfolio may be ignored.

Methods for Measuring and Managing Funding Liquidity Risk and Transaction Liquidity Risk

We say that a given asset is liquid if it resembles money in that it can be exchanged for other goods and assets immediately and at a particular value. Money is a liquid asset. On the other hand, non-money assets have to be liquidated before they can be exchanged for other assets as we do not live in a barter trade economy. However, liquidating no money assets takes some time and the sale proceeds are uncertain to some extent.

Transaction liquidity refers to the ability to buy or sell an asset without moving its price. When an order to buy an asset is large, it causes a substantial short-term imbalance between the demand and supply of the asset leading to price changes. This causes a lack of market liquidity implying that a market participant may be locked into a losing position.

Causes of Transactions Liquidity Risk

Transaction liquidity risk is due to costs, including the cost of searching for a counterparty, market institutions that assist in the search, and inducing someone else to hold a position. These market microstructure fundamentals can be classified as follows:

• Trade processing costs: These are costs associated with finding a counterparty on time. Although these costs may form a significant part of the transaction costs, it is unlikely to increase the liquidity risk unless the trading system gets affected either by human-made circumstances.
• Inventory management of the dealers: Dealers provide trade immediacy to other market participants. Therefore, dealers must hold short or long inventories of assets. Holding inventories exposes dealers to price risk and thus requires compensation. This risk is a volatility exposure and is analogous to short-term option risk.
• Adverse selection: A dealer is compensated by bid-ask spread for the risk of dealing with uninformed vs. well-informed traders.
• Differences of opinion: When market participants (investors) agree on the correct price or about how to interpret new information about specific assets, it becomes more difficult to find a counterparty relative to when the investors disagree.

Different market organizations have different microstructure fundamentals. For example, in a quote-driven system, typically found in OTC markets, certain intermediaries are obliged to post two-way prices publicly and to buy or sell the asset at those prices within known transaction size limits. These intermediaries must hold long or short inventories of the asset and trade heavily to redistribute inventories of securities and thus ultimately reduce them. On the contrary, order-driven systems, typically found on regulated exchanges, are more similar to a perfectly competitive auction model. Usually, the best bids and offers are matched, where possible, throughout the trading session.

Characteristics of Market Liquidity

To better understand the causes of illiquidity, we look at the primary characteristics of asset liquidity used to measure market liquidity.

• Tightness: This refers to the cost of a round-trip transaction, measured by the bid-ask spread and brokers’ commissions. The smaller the spread, the tighter it is, and thus the higher the liquidity.
• Depth: Depth describes how large a transaction it takes to move the market significantly. If a large institution sells, it is most likely to impact the price adversely.
• Resiliency: It refers to the length of time it takes a lumpy order to move the market away from the equilibrium price. In other words, it refers to the ability of the market to bounce back from temporary incorrect prices.

Both depth and resiliency affect the immediacy of a market participant to execute a transaction. Illiquidity manifests itself in observable hard-to-measure ways such as the bid-ask spread, which introduces liquidity risk when it fluctuates. Moreover, adverse price impact is the impact on the equilibrium price of the trader’s activity. Finally, slippage is the deterioration in the market price triggered by the amount of time it takes to get a trade done. If the market is trending, it can go against the trader, even if the order is not large enough to influence the market.

In summary, we need to focus on the fluctuation of the bid-ask spread, the trader’s actions impact on the price of the asset, and the deterioration of the asset price by the time trade happens. Liquidity risk is complicated to measure. However, since the 2007-2009 financial crisis, more attention is being paid to measuring liquidity risks in a firm.

Expected Transactions Cost and the Spread Risk Factor

Daily changes in the bid-ask spread can be assumed to follow a normal distribution with a mean of zero and a constant variance. The zero-mean assumption is unobjectionable since bid-ask spreads cannot rise indefinitely or shrink to 0. The expected transactions cost is half-spread which is expressed as follows:

$$ {\text E}({\text P}_{{\text t}+1} ) \cfrac {\bar {\text s}}{2} $$

Where:

P= Asset midprice.

$$ {\text s}=\cfrac {2(\text{Ask price}-\text{Bid price})}{\text{Ask price}+\text{Bid price}}=\cfrac {\text{Ask price}-\text{Bid price}}{\text{Midprice}} $$

\(\bar {\text s}\)= Estimate of the expected Bid-ask spread

P = Asset midprice.

Following the zero mean normality assumption, \({\text s}=\bar {\text s}\). The 99% confidence interval on transaction cost in dollars is then:

$$ \pm {\text P}\times\cfrac {1}{2} ({\text s}+2.33\sigma_{\text s} ) $$

Where

P = Estimate of the following day asset midprice, typically set to P, which is utmost price observation.

s = Expected bid-ask spread calculated as: \(\frac {\text{ask price-bid price}}{\text{midprice}}\)

\(\sigma_{\text s}\) = sample standard deviation of the spread

The \(\cfrac {1}{2} ({\text s}+2.33\sigma_{\text s} )\) component is known as the 99% spread risk factor.

Example: Calculating Transactions Cost

XYZ Ltd. traded at an asking price of $150 and a bid price of $149. The standard deviation (sample) of the spread is 0.0003. Calculate the expected transaction cost and the 99% spread risk factor for a transaction.

Solution

$$ \text{Midprice (P)}=\cfrac {150+149}{2}=149.50 $$

$$ {\text s}=\cfrac {150-149}{149.5}=0.00669 $$

$$ \text{Transactions cost}=149.50×\cfrac {1}{2} (0.00669+2.33(0.0003))=0.55225 $$

$$ 99\% \text{ spread risk factor}=\cfrac {1}{2} (0.00669+2.33(0.0003))=0.003694 $$

Measuring the Risk of Adverse Price Impact

Liquidity-adjusted VaR is a tool used to measure the risk of adverse price impact. The trader begins by estimating the number of trading days (T) required for the orderly liquidation of a position. Assuming the position can be divided into equal parts across the number of trading days and liquidated at the end of the trading day, a trader would face a 1-day holding period on the entire position, a 2-day holding period on a fraction \(\frac {{\text T}-1}{\text T}\) of the position, a 5-day holding period on a fraction \(\frac {{\text T}-4}{\text T}\) of the position, and so on.

The VaR of the 1-day position adjusted by the square root of time is estimated for a given position as:

$$ \text{VaR}_{\text t}×\sqrt{{\text T}} $$

However, the above formula leads to an overstated VaR; the VaR has to be higher than the one-day position VaR, but less than the one-day position \(\text{VaR}×\sqrt{{\text T}}\) to adjust to the fact that the position could be liquidated over days, the following formula can be used:

$$ \text{VaR}_{\text t}×\sqrt{\cfrac {(1+{\text T})(1+2{\text T})}{6{\text T}}} $$

For example, if the trader estimates that the position can be liquidated in six trading days (T = 6), the adjustment to the overnight VaR of the position is 1.5899, which means that the trader should increase VaR by 59%. This is higher than the initial 1-day VaR but less than the 1-day VaR adjusted by the square root of T.

Interactions between Various Types of Liquidity Risk and Impact on Systemic Risk

As discussed in the previous sections, liquidity has two essential forms of risk. Transactions (or market) liquidity risk is the risk of buying or selling an asset that results in an adverse price movement. On the other hand, funding liquidity risk (balance sheet risk) occurs when a borrower’s credit position is deteriorating or perceived by market participants to be deteriorating. Systemic risk is the risk of failure of the entire financial system due to heavy financial stress.

Different types of liquidity risks are interrelated, and this accelerates problems. For example, if a counterparty increases collateral requirements, the investor may have to unwind it before the full realization of the expected return. Reducing the trade horizon causes deterioration of funding liquidity, which increases the transaction liquidity risk.

A key mechanism that links funding and transaction liquidity is leverage. An investor with a long position may be forced to sell an asset if it can no longer fetch funding. This, in turn, decreases the number of potential asset holders, leading to a reduction in asset valuation. This depresses the asset price, regardless of its expected future cash flows. This decline can be temporary; however, if the length of the depressed asset price is long, it can adversely impact the solvency of the investor who initially purchased the asset

A rapid deleveraging of assets causes a “debt-deflation crisis.” Transaction liquidity could also constrain funding liquidity. For example, if a hedge fund is facing redemptions, it is forced to raise cash by selling assets and, therefore, must decide which assets to sell first. The fundamental trade-off is that by selling the most liquid assets first, the investor incurs the smallest adverse impact. However, he/she is left with a more illiquid portfolio with which to face any continuing funding liquidity pressure. If instead, he sells illiquid assets first, the realized losses increase the real or perceived risk of insolvency, and may, therefore, worsen the funding liquidity pressure.

The level of economy-wide liquidity directly impacts the level of systemic risk. When market conditions deteriorate, liquidity tends to become constrained when investors need it the most. Problems in payments, clearing, and settlement systems are some of the channels through which liquidity risk events can become systemic risk events. Severe stress to the financial system would affect investors simultaneously, suggesting that the illiquidity of one counterparty may have an economic domino effect on other investors throughout the system.

Question

Melinda is the Chief Risk Officer at Titan Investments, a diversified financial services firm. During a strategy meeting, the discussion shifts to the recent acquisition of a hedge fund with a high degree of leverage. Some board members express their concerns about the increased risks due to this leverage, while others emphasize the potential returns. Melinda decides to give a brief presentation on the relationship between leverage and a firm’s return profile, focusing on the leverage effect.

Which of the following statements about the leverage effect is correct?

A. Higher leverage always increases the firm’s return on equity irrespective of the performance of its assets.

B. The leverage effect describes how firms with higher leverage are less susceptible to external market shocks.

C. As leverage increases, both the potential for higher returns and the risk of larger losses magnify.

D. The leverage effect implies that the risk of a firm decreases proportionally as leverage is increased.

Solution

The correct answer is C.

C is correct: As leverage increases, a firm’s potential for both higher returns and larger losses is magnified. This means that while the firm can achieve higher return on equity with successful investments, it also becomes more vulnerable to larger losses if those investments do not perform well. This amplification effect is central to understanding the implications of leverage on a firm’s return profile.

A is incorrect: While higher leverage can increase a firm’s return on equity when its assets perform well, it can also amplify losses when those assets perform poorly. Hence, it’s incorrect to state that higher leverage always increases the firm’s return on equity.

B is incorrect: The leverage effect does not imply that firms with higher leverage are less susceptible to external market shocks. In fact, highly leveraged firms can be more vulnerable to market shocks because their equity cushion (relative to their liabilities) is smaller.

D is incorrect: The leverage effect does not imply a proportional decrease in risk as leverage increases. Rather, as leverage increases, the risk to equity holders tends to increase due to the reduced equity cushion relative to liabilities.

Things to Remember

• The leverage effect speaks to the amplification of potential returns and losses due to the use of leverage.
• Leverage doesn’t inherently guarantee higher returns on equity; it amplifies the outcome, whether positive or negative.
• Firms that employ higher leverage can be more vulnerable to market shocks, especially if their equity base (compared to liabilities) is small.