Laddered Bond Portfolio

When deciding on the best structure for a fixed-income portfolio, managers rely on essential metrics like duration and convexity. While various portfolio setups have similar interest rate exposure, their convexities differ. Convexity, combined with the manager’s interest rate outlook, guides the choice of one structure over another. Here are three common types:

• Bullet Portfolios.
• Barbell Portfolios.
• Laddered Portfolios.

Each of these structures offers distinct advantages depending on a manager’s risk preferences and market conditions.

Bullet Portfolio

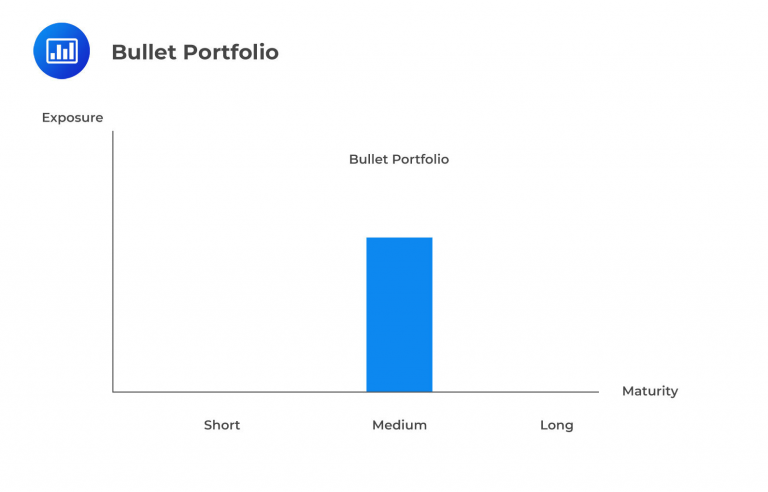
Among the three portfolio setups discussed here, the bullet portfolio is the most straightforward. It’s called a bullet portfolio because it consists of bonds that all mature at the same point on the yield curve. In essence, it’s a portfolio concentrated at one specific maturity, representing a single point in time. This simplicity comes with low convexity, meaning cash flows are entirely concentrated, with no dispersion.

Barbell Portfolio

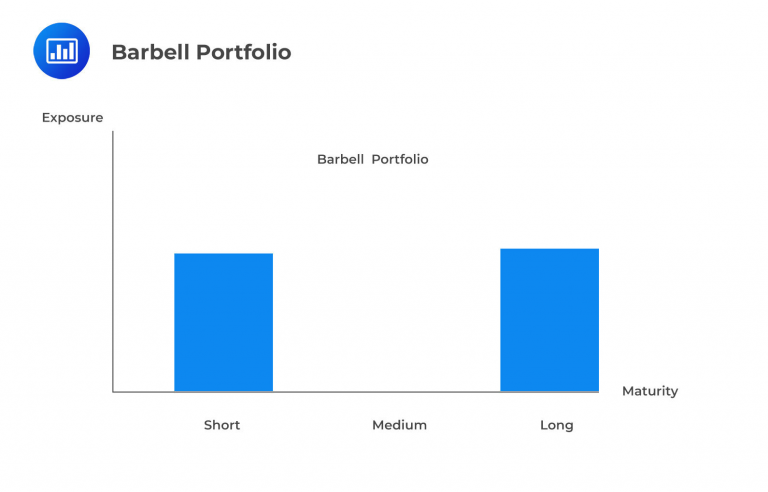
Moving up in complexity, we have the barbell portfolio, which is essentially a combination of two bullet portfolios. In simpler terms, it includes both short-duration and long-duration bonds while avoiding medium-term duration bonds. This diversification of bond maturities spreads out the timing of cash flows, increasing the portfolio’s convexity compared to a bullet portfolio.

Laddered Portfolio

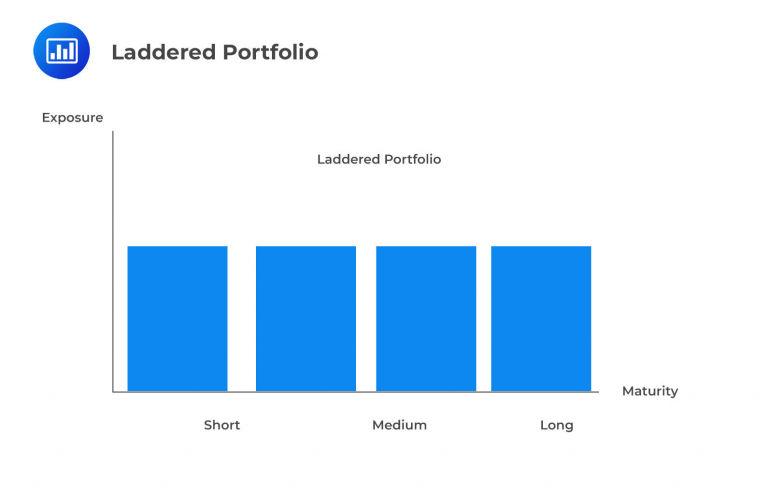
Laddered portfolios involve holding multiple bonds within a single portfolio, distributing them fairly evenly across different maturities. This approach results in the highest cash flow dispersion and convexity among the three portfolio types.

Advantages of Laddering a Portfolio

In this section, we’ll explore the benefits of using laddered portfolios for bond investments. Bond ladders are favored for several reasons:

• Natural Liquidity: Laddered portfolios always have bonds maturing relatively soon (compared to bullet or barbell setups). This ensures that bonds mature and pay their largest cash flows periodically. It’s particularly advantageous when dealing with bonds with wide bid-ask spreads, and the near-term bonds can also serve as collateral for better borrowing rates.
• Time Diversification: Laddering spreads cash flows evenly along the yield curve, reducing the risk of overexposure to sudden changes in the yield curve.
• Dollar Cost Averaging: As near-term bonds mature and return their initial par value, the cash flows can be reinvested systematically within the ladder. Dollar-cost averaging benefits investors because the same amount of money can buy more bonds when prices are low and fewer when prices are high, leading to favorable outcomes.
• Increased Convexity: Laddered portfolios offer the highest level of convexity because cash flows are as dispersed as possible compared to bullet and barbell portfolios. Convexity helps soften price declines and accelerates price appreciation, providing an additional layer of risk management.

Alternative to Constructing a Bond Portfolio of Individual Bonds

For those who prefer an alternative approach to building a bond portfolio with individual bonds, there are options:

• Target date bond ETFs: Investors can opt for target-date bond ETFs, which aim to mimic the performance of bonds with specific maturities using a passive management strategy. These ETFs offer advantages for smaller investors, such as benefiting from economies of scale seen in larger funds and experiencing enhanced liquidity when trading their shares.
• Passively managed indexes: Some investors may find passively managed indexes without specific maturity dates more suitable. These indexes have indefinite lifespans, offering increased diversification and liquidity, even when compared to target-date ETF funds. This approach provides flexibility and a longer investment horizon.

Question

Which of the following portfolio types is least likely associated with high convexity?

1. Barbell.
2. Bullet.
3. Ladder.

Solution

The correct answer is B.

A bullet portfolio consists of bonds that have the same maturity or a similar maturity, typically with no significant variation in maturities. Bullet portfolios are often associated with lower convexity because they lack the dispersion in maturities that can contribute to higher convexity. Therefore, a bullet portfolio is less likely to be associated with high convexity.

A is incorrect. A barbell portfolio consists of a combination of short-term and long-term bonds, with little or no intermediate-term bonds. The presence of long-term bonds in a barbell can result in high convexity because long-term bonds tend to have higher convexity due to their longer maturities. Therefore, a barbell portfolio is typically associated with high convexity.

C is incorrect. A ladder portfolio consists of bonds with various maturities, evenly spaced along the yield curve. Ladder portfolios are designed to have moderate convexity. The combination of short, intermediate, and long-term bonds in a ladder can help balance convexity and interest rate risk. Ladder portfolios aim to provide a middle-ground solution between low and high convexity.

Reading 20: Liability-Driven and Index-Based Strategies

Los 20 (d) Describe the construction, benefits, limitations, and risk–return characteristics of a laddered bond portfolio