Joint Hypotheses Testing

In multiple regression, the intercept in simple regression represents the expected value of the dependent variable when the independent variable is zero, while in multiple regression, it’s the expected value when all independent variables are zero. The interpretation of slope coefficients remains the same as in simple regression.

Tests for single coefficients in multiple regression are similar to those in simple regression, including one-sided tests. The default test is against zero, but you can test against other hypothesized values.

In some cases, you might want to test a subset of variables jointly in multiple regression, comparing models with and without specific variables. This involves a joint hypothesis test where you restrict some coefficients to zero. To test  the slope against a hypothesized value other than zero we will need to:

• You can conduct the test by either modifying the hypothesized parameter value, B_j, in the test statistic or
• by comparing B_j with the confidence interval boundaries derived from the regression coefficient output.

At times, we may want to collectively test a subset of variables within a multiple regression. To illustrate this concept and set the stage, let’s say we aim to compare the regression outcomes for a portfolio’s excess returns using Fama and French’s three-factor model (MKTRF, SMB, HML) with those using their five-factor model (MKTRF, SMB, HML, RMW, CMA). Given that both models share three factors (MKTRF, SMB, HML), the comparison revolves around assessing the necessity of the two additional variables: the return difference between the most profitable and least profitable firms (RMW) and the return difference between firms with the most conservative and most aggressive investment strategies (CMA). The primary goal in determining the superior model lies in achieving simplicity by identifying the most effective independent variables in explaining variations in the dependent variable.

Now, let’s contemplate a more comprehensive model:

$$Y_i= b_0+b_1 X_1i+b_2 X_2i+b_3 X_3i+b_4 X_4i+b_5 X_5i+ε_i$$

The model above has five independent variables and it is referred to as the unrestricted model. Sometimes we may want to test whether and together have no significant contribution used to explain the dependent variable, i.e\(X_4\) =\(X_5\)=0. We compare the full model (unrestricted model) to:
$$Y_i= b_0+b_1 X_1i+b_2 X_2i+b_3 X_3i+ε_i$$
This is referred to as the restricted model because it excludes \(X_4\) and \(X_5\), which will have the effect of restricting the slope coefficients on \(X_4\) and \(X_5\) to be equal to 0. These models are also termed nested models because the restricted model is contained within the unrestricted model. This model comparison entails a null hypothesis that encompasses a combined restriction on two coefficients, namely, \(H_0:b_4=b_5=0\) against \(H_A:b_4\) or \(b_5≠0\)

We employ a statistic to compare nested models, pitting the unrestricted model against a restricted version with some slope coefficients set to zero. This statistic assesses how the joint restriction affects the restricted model’s ability to explain the dependent variable compared to the unrestricted model. We test the influence of omitted variables jointly using an F-distributed test statistic.
$$F=\frac{(\text{Sum of squares error restricted model}-\text{Sum of squares error unrestricted})/q}{(\text{Sum of squares error unrestricted model})/(n-k-l)}$$

Where

\(q\)= Number of restrictions

When we want to compare an unrestricted model to a restricted model \(q\)=2 because we are testing the null hypothesis of \(b_4=b_5=0\).The F-statistic has \(n-k-1\)  and \(q\) degrees of freedom. In summary, the unrestricted model includes a larger set of explanatory variables, whereas the restricted model has \(q\) fewer independent variables because the slope coefficients of the excluded variables are forced to be zero.

Why not just conduct hypothesis tests for each individual variable and make conclusions based on that data? In many cases of multiple regression with financial variables, there’s typically some level of correlation among the variables. As a result, there may be shared explanatory power that isn’t fully accounted for when testing individual slopes.

Example

Table 1: Partial ANOVA Results for Models Using Three and Five Factors
$$ \begin{array}{c|c|c|c|c} \textbf{Source}& \textbf{Factors} & \textbf{Residual} & \textbf{Mean }&\textbf{Degrees} \\ & \textbf{} & \textbf{sum of squares}& \textbf{squares errors}&\textbf{of freedom }\\ \hline \text{Restricted} & 1,2,3 & 66.9825 & 1.4565 & 44 \\ \hline \text{Unrestricted} & 1,2,3,4,5 & 58.7232 & 1.3012 & 42\\ \hline\end{array} $$

Test of Hypothesis for factors 4 and 5 at 1% Level of significance

Step1: State the hypothesis
            \(H_0:b_4=b_5=0\) vs. \(H_a:\) at least \(b_j≠0\)

Step 2: Identify the appropriate test statistic.
$$F=\frac{(\text{Sum of squares error restricted model}-\text{Sum of squares error unrestricted})/q}{(\text{Sum of squares error unrestricted model})/(n-k-l)}$$

Step 3: Specify the level of significance.

            \(α\)=1% (one-tail, right side)

Step 4: State the decision rule.

            Critical F-value = 5.149. Reject the null if the calculated F-statistic

            exceeds 5.149.

Step 5: Calculate the test statistic.
$$F=\frac{(66.9825-58.7232)/2}{58.7232/42}=\frac{4.1297}{1.3982}=2.9536$$

Step 6: Make a decision

            Fail to reject the null hypothesis since the answer is less than the critical f-

            value.

Hypothesis testing involves testing an assumption regarding a population parameter. A null hypothesis is a condition believed to be false. We reject the null hypothesis in the presence of enough evidence against it and accept the alternative hypothesis.

Hypothesis testing is performed on the estimated slope coefficients to establish if the independent variables explain the variation in the dependent variable.

The t-statistic for testing the significance of the individual coefficients in a multiple regression model is calculated using the formula below:

$$ t=\frac{\widehat{b_j}-b_{H0}}{S_{\widehat{b_j}}} $$

Where:

\(\widehat{b_j}\) = Estimated regression coefficient.

\(b_{H0}\) = Hypothesized value.

\(S_{\widehat{b_j}}\) = The standard error of the estimated coefficient.

It is important to note that the test statistic has \(n-k-1\) degrees of freedom, where \(k\) is the number of independent variables and 1 is the intercept term.

A t-test tests the null hypothesis that the regression coefficient equals some hypothesized value against the alternative hypothesis that it does not.

$$ H_0:b_j=v\ vs\ H_a:b_j\neq v $$

Where:

\(v\) = Hypothesized value.

The F-test determines whether all the independent variables help explain the dependent variable. It is a test of regression’s overall significance. The F-test involves testing the null hypothesis that all the slope coefficients in the regression are jointly equal to zero against the alternative hypothesis that at least one slope coefficient is not equal to 0.

i.e.: \(H_0: b_1 = b_2 = … = b_k = 0\) versus \(H_a\): at least one \(b_j\neq 0\)

We must understand that we cannot use the t-test to determine whether every slope coefficient is zero. This is because individual tests do not account for interactions among the dependent variables.

The following inputs are required to determine the test statistic for the null hypothesis.

1. The total number of observations, \(n\).
2. The total number of slope coefficients to be estimated, \(k+1\), where \(k\) = number of slope coefficients.
3. The residual sum of squares (SSE), which is the unexplained variation.
4. The regression sum of squares (RSS), which is the explained variation.

The F-statistic (which is a one-tailed test) is computed as:

$$ F=\frac{\left(\frac{RSS}{k}\right)}{\left(\frac{SSE}{n- \left(k + 1\right)}\right)}=\frac{\text{Mean Regression sum of squares (MSR)}}{\text{Mean squared error(MSE)}} $$

Where:

• \(RSS\) = Regression sum of squares.
• \(SSE\) = Sum of squared errors.
• \(n\) = Number of observations.
• \(k\) = Number of independent variables.

A large value of \(F\) implies that the regression model explains variation in the dependent variable. On the other hand, the value of \(F\) will be zero when the independent variables do not explain the dependent variable.

The F-test is denoted as \(F_{k,(n-\left(k+1\right)}\). The test should have \(k\) degrees of freedom in the numerator and \(n-(k+1)\) degrees of freedom in the denominator.

Decision Rule

We reject the null hypothesis at a given significance level, \(\alpha\), if the calculated value of \(F\) is greater than the upper critical value of the one-tailed \(F\) distribution with the specified degrees of freedom.

I.e., reject \(H_0\) if \(F-\text{statistic}> F_c (\text{critical value})\). Graphically, we see the following:

Example: Calculating and Interpreting the F-statistic

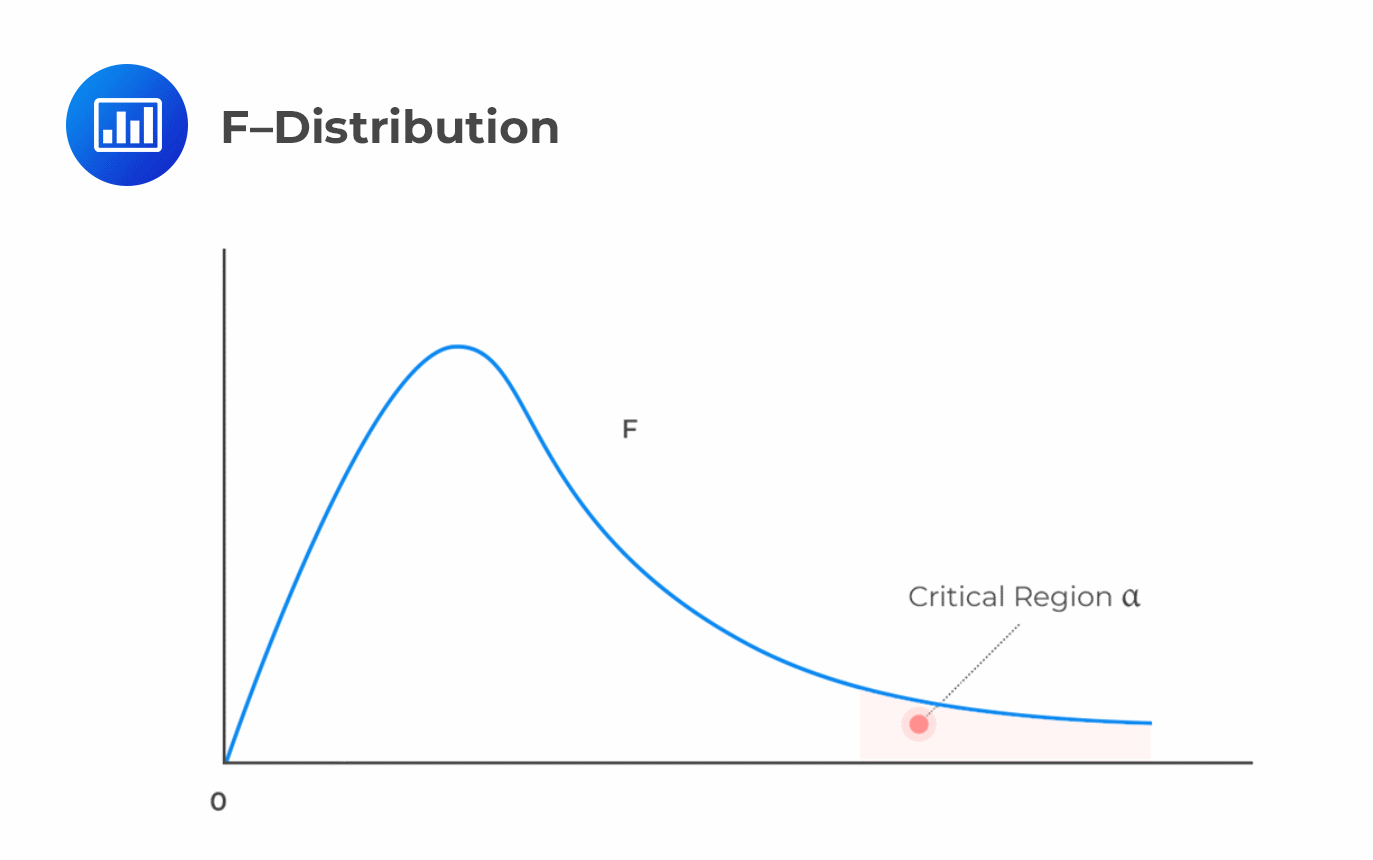
The following ANOVA table presents the output of the multiple regression analysis of the price of the US Dollar index on the inflation rate and real interest rate.

$$ \textbf{ANOVA} \\ \begin{array}{c|c|c|c|c|c} & \text{df} & \text{SS} & \text{MS} & \text{F} & \text{Significance F} \\ \hline \text{Regression} & 2 & 432.2520 & 216.1260 & 7.5405 & 0.0179 \\ \hline \text{Residual} & 7 & 200.6349 & 28.6621 & & \\ \hline \text{Total} & 9 & 632.8869 & & & \end{array} $$

Test the null hypothesis that all independent variables are equal to zero at the 5% significance level.

Solution

We test the null hypothesis:

\(H_0: \beta_1= \beta_2 = 0\) verses \(H_a:\) at least one \(b_j\neq 0\)

with the following variables:

Number of slope coefficients: \((k) = 2\).

Degrees of freedom in the denominator:  \(n-(k+1) = 10-(2+1) = 7\).

Residual sum of squares: \(RSS = 432.2520\).

Sum of squared errors: \(SSE = 200.6349\).

Thus,

$$ F=\frac{\left(\frac{RSS}{k}\right)}{\left(\frac{SSE}{n- \left(k + 1\right)}\right)}=\frac{\frac{432.2520}{2}}{\frac{200.6349}{7}}=7.5405 $$

For \(\alpha= 0.05\), the critical value of \(F\) with \(k = 2\) and \((n – k – 1) = 7\) degrees of freedom \(F_{0.05, 2, 7,}\) is approximately 4.737.

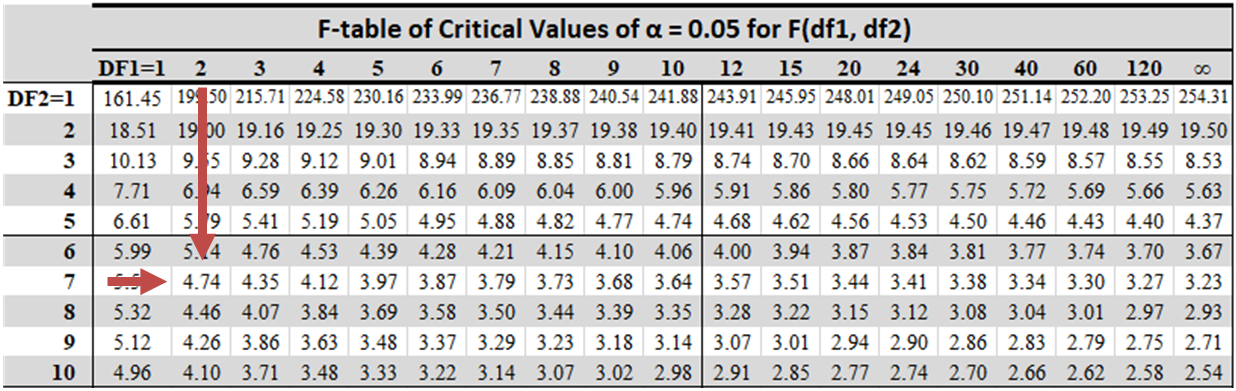The calculated value of the F-test statistic, 7.5405, is greater than the critical value of F, 4.737. We, therefore, reject the null hypothesis that the coefficients of both independent variables equal 0.

Additionally, you will notice that from the ANOVA table, the column “Significance F” reports a p-value of 0.0179, which is less than 0.05. The p-value implies that the smallest level of significance at which the null hypothesis can be rejected is 0.0179.

Analyzing Multiple Regression Models for Model Fit

$$ \begin{array}{l|l} \textbf{Statistic} & \textbf{Assessing criteria} \\ \hline {\text{Adjusted } R^2} & \text{It is better if it is higher.} \\ \hline \text{Akaike’s information criterion (AIC)} & \text{It is better if it is lower.} \\ \hline {\text{Schwarz’s Bayesian information} \\ \text{criterion (BIC)}} & \text{A lower number is better.} \\ \hline {\text{An analysis of slope coefficients using} \\ \text{the t-statistic}} & {\text{The critical t-value(s) are located} \\ \text{outside the given range for the} \\ \text{selected significance level.}} \\ \hline {\text{Test of slope coefficients using the} \\ \text{F-test}} & {\text{The F-value for the selected} \\ \text{significance level exceeds the} \\ \text{critical value.}} \end{array} $$

Note that:

• Several models that explain the same dependent variable are evaluated using Akaike’s information criterion (AIC). Often, it can be calculated from the information in the regression output, but most regression software includes it as part of the output.

  $$ AIC=n\ ln\left[\frac{\text{Sum of squares error}}{n}\right]+2(k+1) $$

  Where:

  \(n\) = Sample size.

  \(k\) = Number of independent variables.

  \(2\left(k+1\right)\) = The model is penalized when independent variables are included.

• Models with the same dependent variables can be compared using Schwarz’s Bayesian Information Criterion (BIC).

  $$ BIC=n \ ln\left[\frac{\text{Sum of squares error}}{n}\right]+ln(n)(k+1) $$

• Models with more parameters incur a significant penalty, so BIC prefers models with fewer parameters. It is because ln(n) exceeds 2, even for very small sample sizes.

Question

Which of the following statements is most accurate?

1. The best-fitting model is the regression model with the highest adjusted \(R^2\) and low BIC and AIC.
2. The best-fitting model is the regression model with the lowest adjusted \(R^2\) and high BIC and AIC.
3. The best-fitting model is the regression model with both high adjusted \(R^2\) and high BIC and AIC.

Solution

The correct answer is A.

A regression model with a high adjusted \(R^2\) and a low AIC and BIC will generally be the best fit.

B and C are incorrect. The best-fitting regression model generally has a high adjusted \(R^2\) and a low AIC and BIC.