Black Option Valuation Model
The black option valuation model is a modified version of the BSM model... Read More
The value of a CDS depends on the probability of default, i.e., the likelihood of non-payment of promised interest and/or principal on a bond. The default probability typically increases with time. However, in a CDS context, the probability of default is assumed to be conditional over time as each periodic payment is subject to non-payment. Thus, the relevant probability of default is the hazard rate, which is the probability that an event will occur given that it has not already occurred in the past.
Loss given default is the forgone receipt of payment in the event of default. In other words, it is the loss incurred in a non-repayment scenario.
The expected loss is the promised interest and principal payments minus expected recovery weighted by the default probability. i.e.,
$$ \text{Expected loss} = \text{Loss given default} × \text{Probability of default} $$
Consider a $1,000 par value, two-year, 4% annual coupon senior unsecured bond. Assume that the hazard rate on the coupon payment in the first year is 1% and 2% for the final coupon and principal payment, and the recovery rate is 40%.
The probability of default, loss given default, and the expected loss are closest to:
Solution
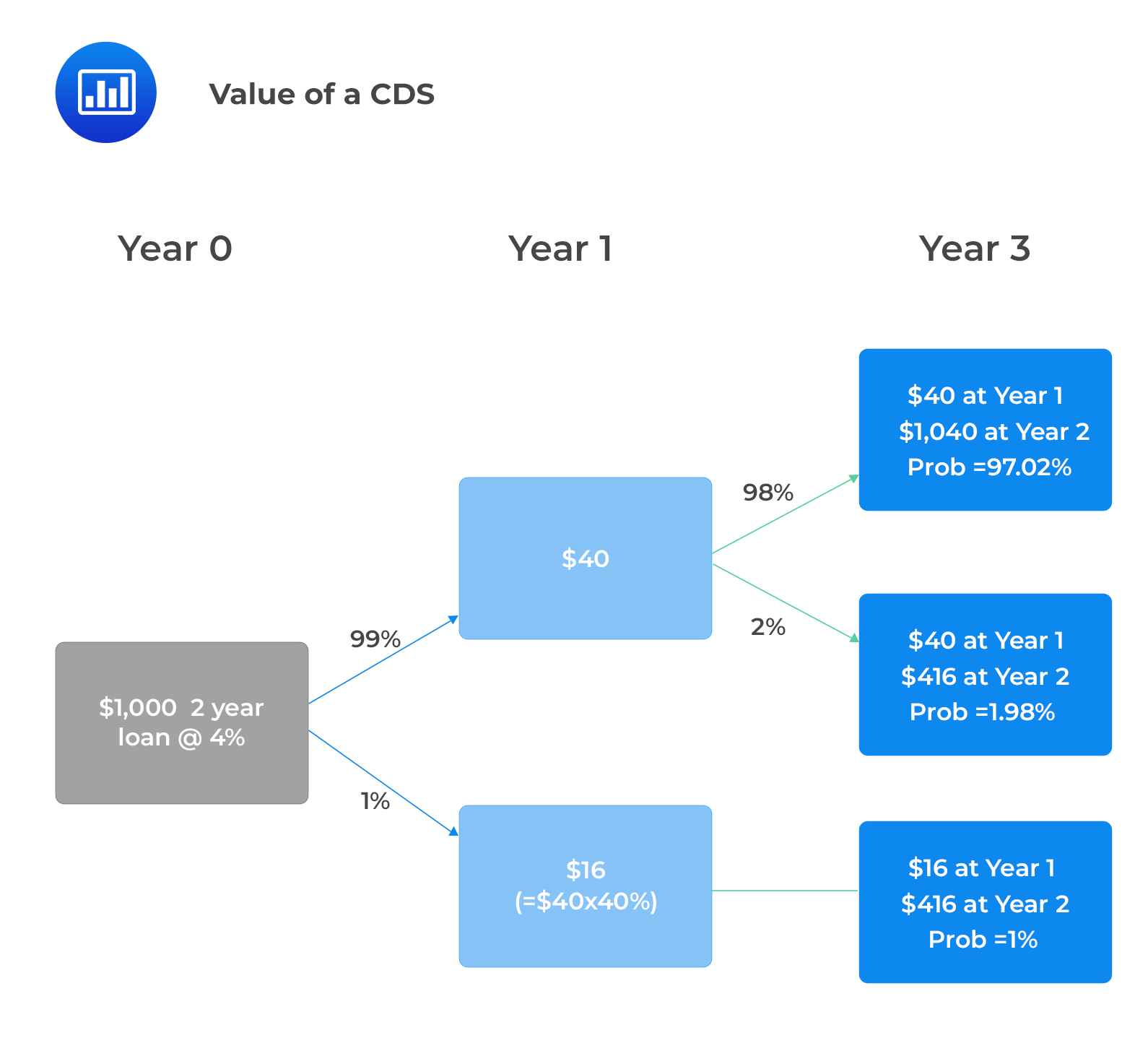 Probability of Default
Probability of Default$$ \text{Probability of survival to maturity} = 99\%\times98\%=97.02\% $$
The probability of default (PD) at some point during the life of the loan is:
$$ PD=100\%-97.02\%=2.98\% $$
If the borrower defaults on the first payment:
$$ \text{Amount lost} = $40-$16 = $24 $$
If the 2nd payment defaults,
$$ \text{Amount lost} = $1,040-$416 = $624 $$
Thus,
$$ \text{Total loss given default} = $624+$24 = $648 $$
However, if the borrower defaults only on the 2nd payment, the loss given default will be $624.
$$ \text{Expected loss} = \text{Loss given default} \times \text{Probability of default} $$
There is a 1% chance of losing $648 and a (0.99) × (0.02) = 0.0198, or 1.98% chance of losing $624.
Thus,
$$ \text{Expected loss}= \left(0.01\right)\times \left($648\right)+ \left(0.0198\right)\times$624=$18.835 $$
CDS contracts have two legs, the premium leg, and the protection leg.
This is a series of payments made by the protection buyer to the protection seller.
These are contingent payments made by the protection seller to the protection buyer in the event of default.
$$ \text{Upfront payment} = \text{PV} \left(\text{Protection Leg}\right)– \text{PV (Premium Leg)} $$
If the difference is greater (less) than zero, the protection buyer (seller) pays the protection seller (buyer)
The market convention for CDS mandates investment-grade debt to have standardized coupons of 1% and 5% for high-yield debt. An upfront premium is paid when credit spreads deviate from standard coupons.
Industry practitioners use the following CDS pricing approximations:
$$ \begin{align*} \text{PV (Credit Spread)} &=\text{Upfront premium} + \text{PV (Fixed Coupon)} \\ \\ \text{Upfront premium} & \approx \text{Credit spread} – \text{Fixed coupon} \times \text{Duration} \\ \\ \text{Credit spread} & \approx \left(\frac{\text{Upfront premium}}{\text{Duration}}\right)+ \text{Fixed coupon} \\ \\ \text{Upfront premium } \% &= 100 – \text{CDS Price in currency per 100 par} \end{align*} $$
ABC Inc. is a high-yield company that pays 4% annual coupons on its CDS. The company’s 15-year credit spread is 500 bps, and the duration of the CDS is 10 years. The approximate upfront premium required to buy a 15-year CDS protection is closest to:
$$ \begin{align*} \text{Upfront premium} & \approx \text{Credit spread} – \text{Fixed coupon} \times \text{Duration} \\ &=\left(5\%-4\%\right) \times10 = 10\% \text{ of the notional} \end{align*} $$
The value of a CDS contract varies depending on the changes to the reference entity’s credit quality, including the default probability and loss given default. Further, the shortening of the duration over time also influences the value of a CDS. For example, a seller of an existing CDS contract gains while the buyer losses when the credit quality improves.
The approximate change in the value of a CDS for a spread or price change is expressed as follows:
$$ \begin{align*} \text{Protection buyer’s profit} &= \Delta \text{spread (bps)} \times \text{Duration} \times \text{Notional} \\ \\ \% {\Delta} \text{CDS price} &= {\Delta} \text{spread (bps)} \times \text{Duration} \end{align*} $$
An investor purchases €5 million of 10-year CDS protection for a CDS contract with a duration of 5 years. The company’s credit spread widens from 200bps to 500bps.
$$ \begin{align*} \% {\Delta} \text{CDS price} &= {\Delta} \text{spread (bps)} \times \text{Duration} \\ &=\left(5\%-2\%\right)\times 5=15\% \end{align*} $$
$$ \begin{align*} \text{Protection buyer’s profit} &= \Delta \text{spread (bps)} \times \text{Duration} \times \text{Notional} \\ &=5\%-3\% \times 5 \times 5 \text{ Million}= €500,000 \end{align*} $$
The change in the price of a CDS contract generates gains or losses which may be monetized upon unwinding the position. Since the protection seller has a long position on credit risk, they gain from the improvement of the credit quality. On the other hand, the protection buyer is short of the credit risk and thus gains when the credit quality deteriorates.
CDS gains/losses can be monetized in either of the following ways:
Question
XYZ has a constant hazard rate of 4% per quarter. An investor sells 3-year CDS protection on the company with the payments made quarterly over the next three years. The probability of default at any given point in time during the first two quarters is closest to:
- 3.84%.
- 4.00%.
- 7.84%.
Solution
The correct answer is C.
The probability of survival is 96% in the first quarter, and the conditional probability of survival through the second quarter is also 96% as the hazard rate is constant at 4% each quarter.
$$ \text{Probability of survival to the second quarter} = 96\% × 96\% = 92.16\% $$
Hence, the probability of default sometime during the first two quarters is \(1 – 92.16% = 7.84%\).
Reading 32: Credit Default Swaps
LOS 32 (c) Explain the principles underlying and factors that influence the market’s pricing of CDS.