Spot and Future Price Comparisons in C ...
Commodity prices are generally represented by: Spot price: Refers to the current price... Read More
A workable approach employed in constructing a suitable yield curve for risky bonds involves adding a fixed Z-spread to the one-year forward rates derived from the default-free spot yield curve.
Recall that Z-spread is the basis point spread that would need to be added to the default-free spot curve to equate the present value of cash flows to the market price of a risky bond.
The same approach can be used to value risky bonds with embedded options. Option-adjusted spread, which is the spread after adjusting for the options risk, is used in this case.
Option-adjusted spread (OAS) is the fixed spread added to the one-year forward rates on the interest rate tree that equates the arbitrage-free value and the market price of a risky bond with embedded options.
Note that the Z-spread for a straight bond is its option-adjusted spread assuming volatility of zero.
$$ \text{Option adjusted spread (OAS)} = \text{Z-Spread} – \text{Option cost.} $$
The above relationship is illustrated in the following figure.
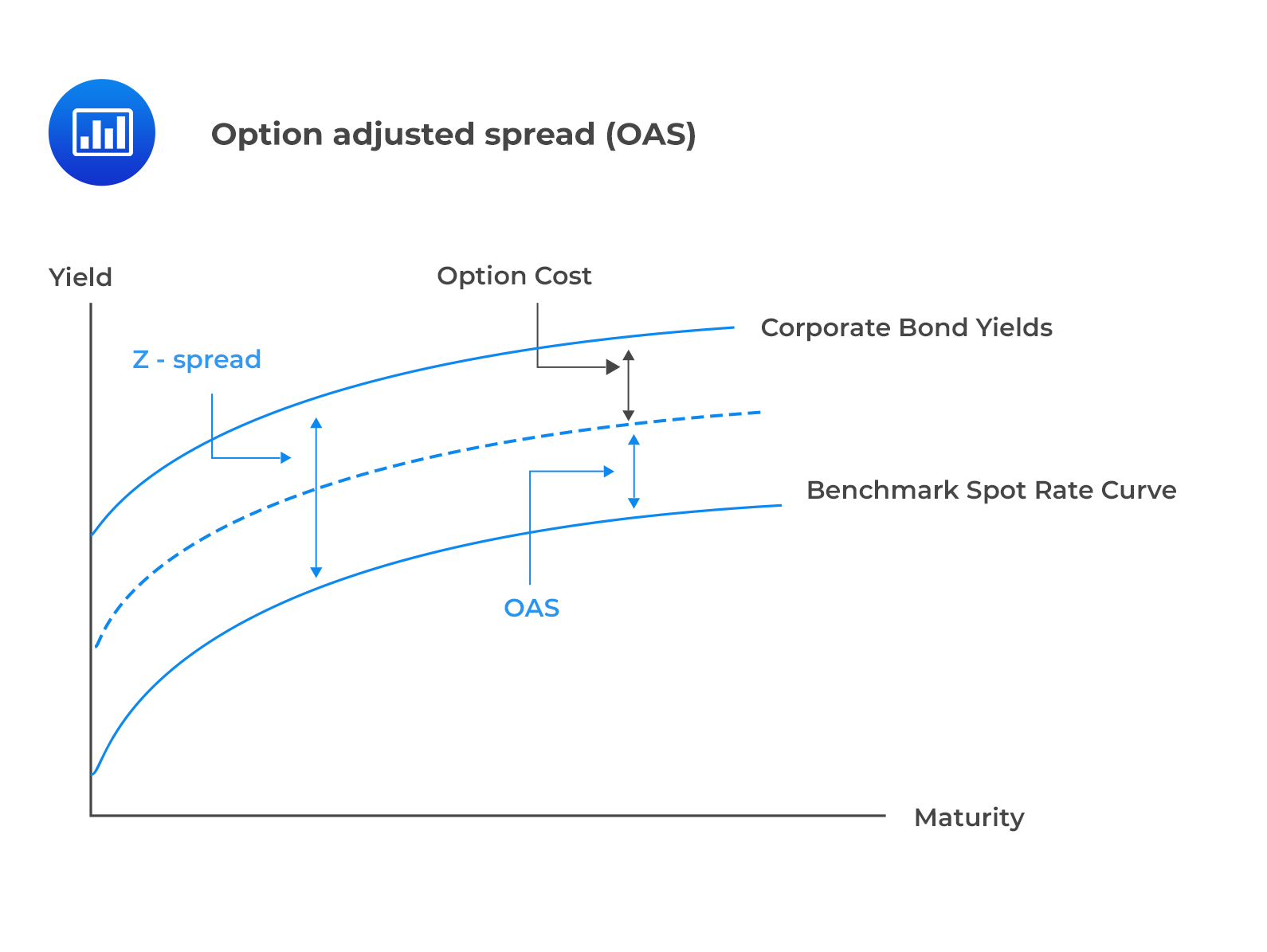 OAS can be used to assess bond relative values. Two bonds with the same characteristics and credit quality must have the same OAS. Otherwise, the bond with the largest OAS is likely to be underpriced (cheap) relative to the bond with the smallest OAS.
OAS can be used to assess bond relative values. Two bonds with the same characteristics and credit quality must have the same OAS. Otherwise, the bond with the largest OAS is likely to be underpriced (cheap) relative to the bond with the smallest OAS.
Further, an OAS equal to that of a comparable bond indicates that the bond is fairly priced.
The following binomial interest rate tree has been calibrated, assuming an interest rate volatility of 15%.
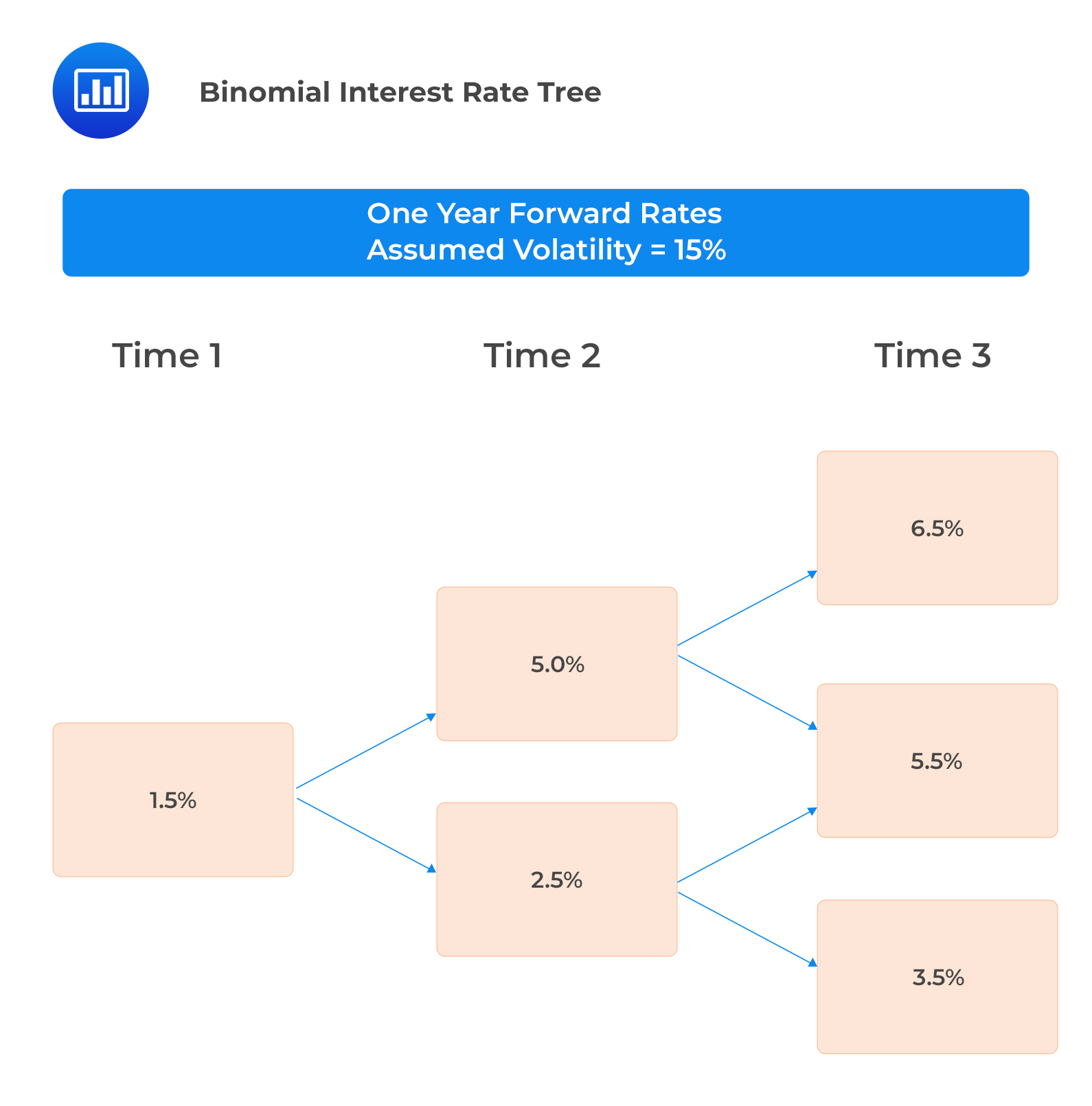 The OAS of a three-year 5% annual coupon risky bond, callable at par one year and two years from now priced at $102.05 can be computed as follows:
The OAS of a three-year 5% annual coupon risky bond, callable at par one year and two years from now priced at $102.05 can be computed as follows:
The value of the bond using the above interest rate tree is $103.00, as shown in the following figure:
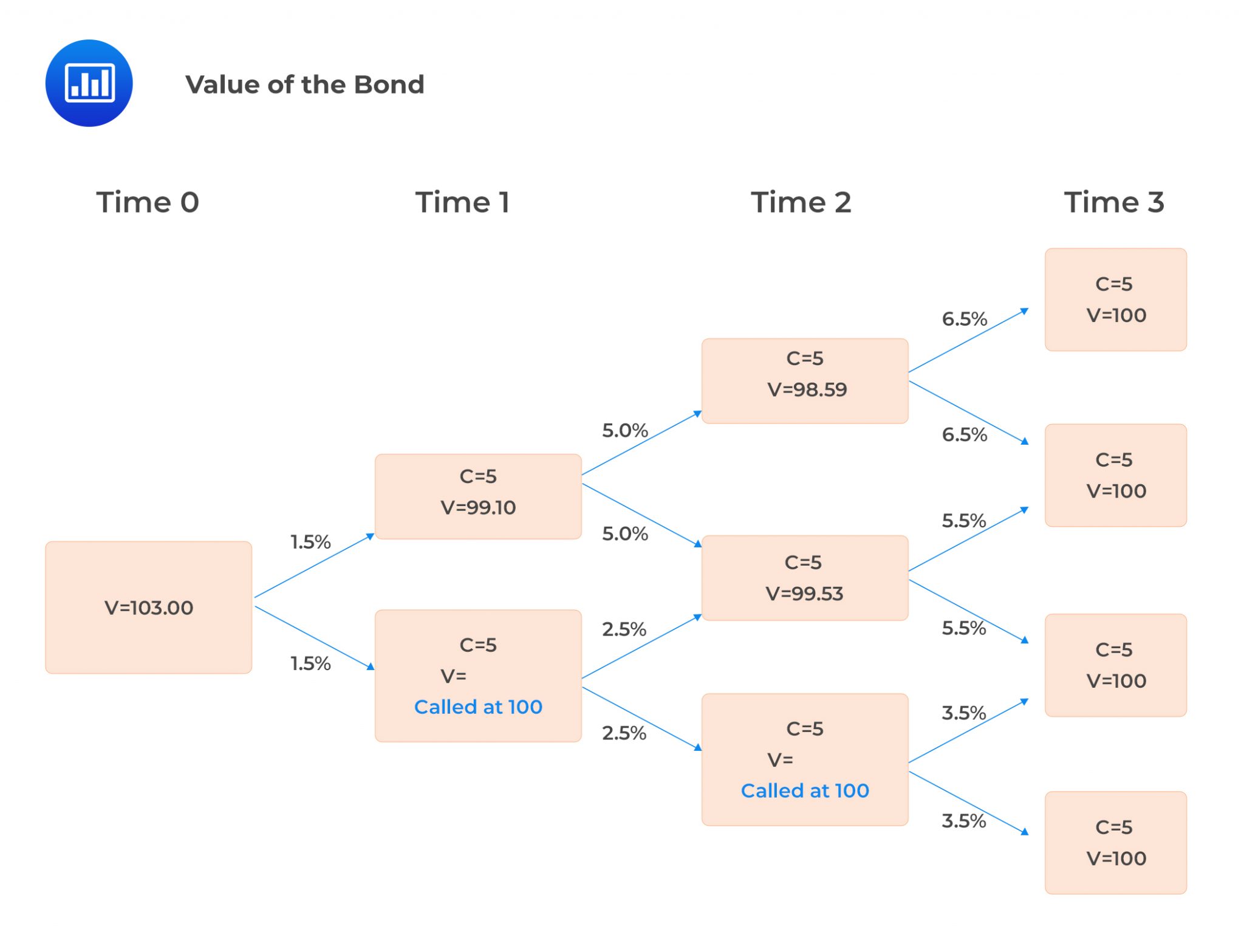 We need to compute the OAS that justifies the current market price of $102.05 by trial and error.
We need to compute the OAS that justifies the current market price of $102.05 by trial and error.
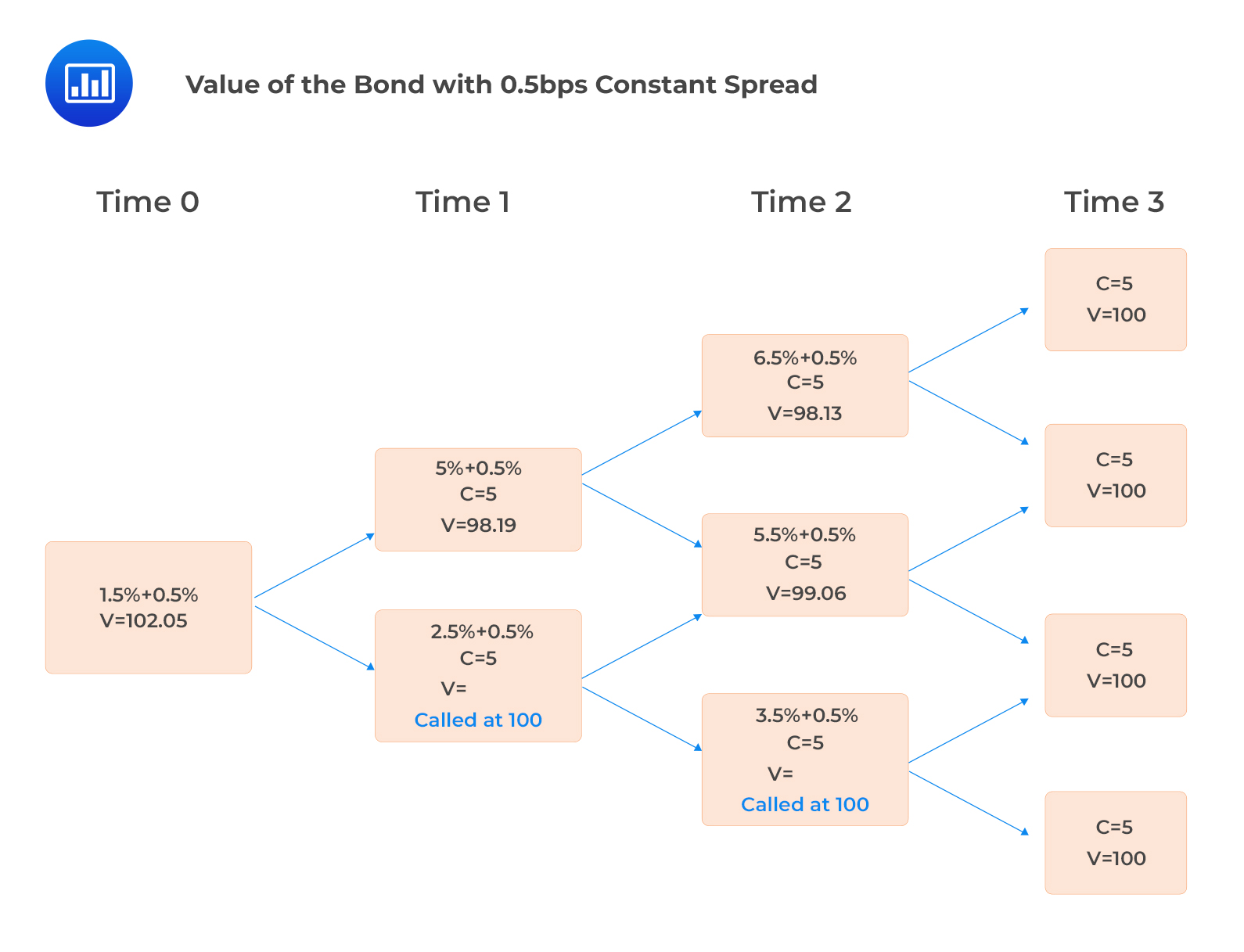
If we add a constant spread (OAS) of 50 bps to each one-period forward rate, we obtain a value of $102.05, which is equal to the current market price, as shown below:
Question
The following information relates to two risky callable bonds with similar characteristics and credit quality.
$$ \begin{array}{c|c} \textbf{Bond} & \textbf{OAS} \\ \hline X & 30\text{bps} \\ \hline Y & 20\text{bps} \end{array} $$
Relative to bond Y, bond X is most likely:
- Underpriced.
- Fairly priced.
- Overpriced.
Solution
The correct answer is A.
An OAS higher than that of a comparable bond indicates that the bond is likely underpriced relative to the other.
In this case, bond X has the largest OAS, indicating that it is likely to be underpriced (cheap) relative to the bond Y with the smallest OAS.
Reading 30: Valuation and Analysis of Bonds with Embedded Options
LOS 30 (g) Explain the calculation and use of option-adjusted spreads.