Application of the Information Ratio

An optimal portfolio can be obtained by combining a risk-free asset with an optimally risky asset portfolio. The optimally risky asset portfolio is the point where the capital allocation line is tangent to the efficient frontier.

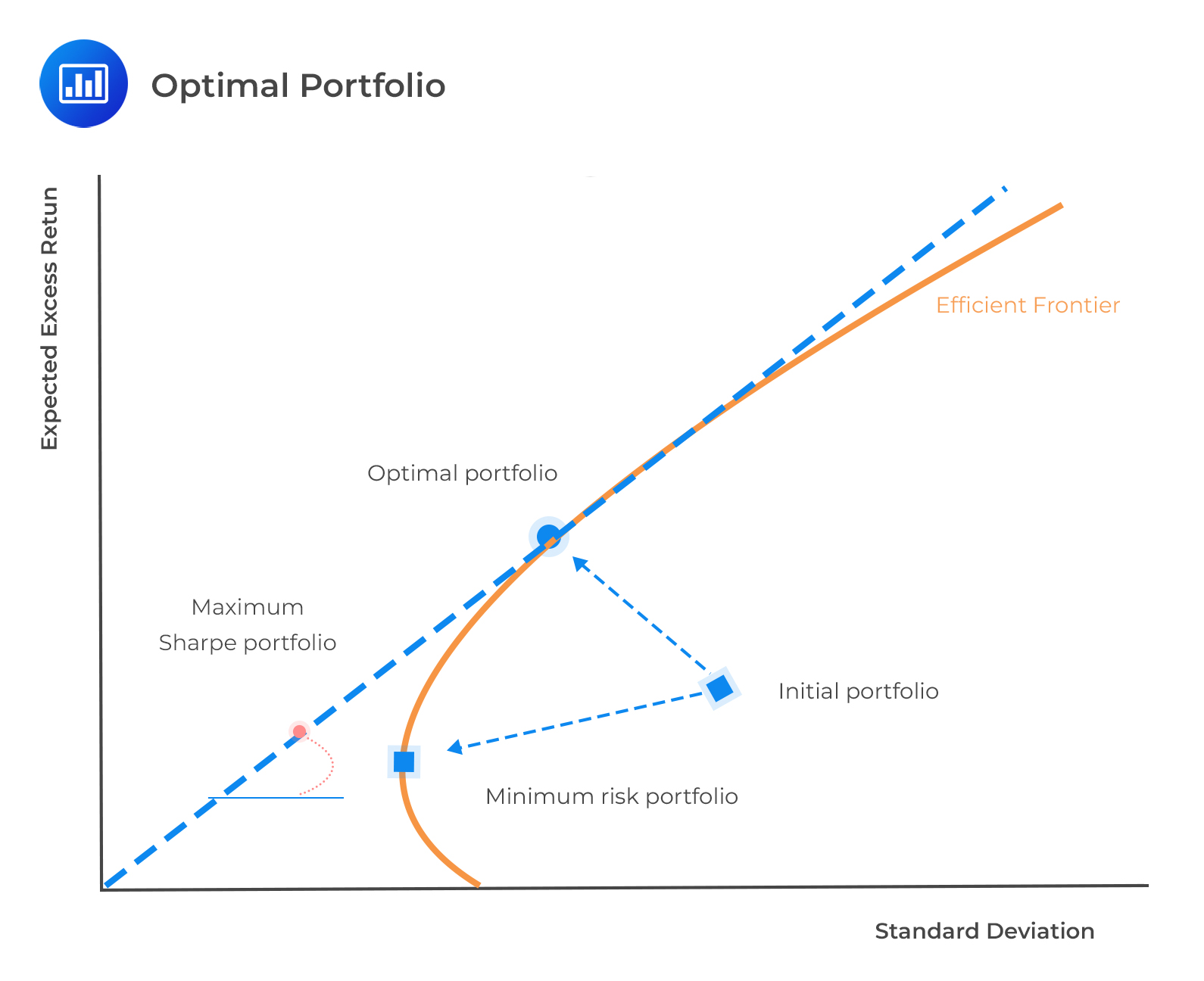The optimal portfolio is the one with the highest possible Sharpe ratio. Therefore, irrespective of an investor’s risk aversion, they need to find a single risky asset portfolio with the highest Sharpe ratio, such that the following equation holds.

$$ SR_P^2=SR_B^2+IR^2 $$

Additionally, the portfolio with the highest information ratio has the highest Sharpe ratio. However, this may not be the ideal case when IR is negative. Consequently, the mean-variance theory asserts that the best criterion for active performance assessment is using the expected information ratio, especially when using the same benchmark.

The information ratio is also applied in the determination of the optimal level of active risk for unconstrained portfolios:

$$ STD\left(R_A\right)=\frac{IR}{SR_B}{STD}(R_B) $$

Example: Optimal Level of Active Risk

Calculate the optimal level of aggressiveness in an actively managed portfolio with an information ratio of 0.20. Further, assume that the benchmark portfolio has a Sharpe ratio of 0.25 and a total risk of 15.0%

Solution

Using the equation:

$$ \begin{align*} STD\left(R_A\right) & =\frac{IR}{SR_B}STD(R_B) \\ STD\left(R_A\right) & =\left(\frac{0.20}{0.25}\right)\times15\%=12.0\%. \\ \end{align*} $$

Question

A portfolio manager uses a benchmark portfolio that has a Sharpe ratio of 0.30 and a total risk of 12.0%. His actively managed portfolio has an information ratio of 0.25 and an active risk of 5.0%. The portfolio’s optimal level of active risk is closest to:

1. 10%.
2. 12%.
3. 15%.

Solution

The correct answer is A.

$$ \begin{align*} STD\left(R_A\right) & =\frac{IR}{SR_B}STD(R_B) \\ STD\left(R_A\right) &=\left(\frac{0.25}{0.30}\right)12.0\%=10.0\%. \end{align*} $$

Reading 44: Analysis of Active Portfolio Management

LOS 44 (d) Explain how the information ratio may be useful in investment manager selection and choosing the level of active portfolio risk.