Calibrating a Binomial Interest Rate Tree

The following steps should be followed when calibrating binomial interest rate trees to match a particular term structure:

• Step 1: Estimate the appropriate spot and forward rates for a known par value curve.
• Step 2: Construct the interest rate tree using the assumed volatility and the interest rate model.
• Step 3: Determine the appropriate values for the zero-coupon bonds at each node using backward induction.
• Step 4: Calibrate the tree to ensure it is arbitrage-free. The value of a bond produced by the interest rate tree must be equal to its market price.

 When constructing an interest rate tree as per step 2 above, it’s important to remember that:

• At each node, the forward interest rates can either go up (higher rate) or down (lower rate).
• You can determine the lower rate iteratively or by solving simultaneous equations depending on:
  • The relationship: \(i_{1,d}=i_{1,u}\times e^{-2\sigma}\).
  • Known spot and forward rates.
  • Features of the coupon bond, particularly its maturity.
• All this can be complicated to perform manually, but some Excel tools, such as Solver, can be employed to make it easy.
• Adjacent forward rates (for the same period) are two standard deviations apart. this means that if you know one of the forward rates for a particular nodal period, you can easily compute the other forward rates for that period in the tree.

The following related formulas are important to remember:

$$i_{1,u}=i_{1,d}e^{2\sigma }$$

$$i_{2,uu}=i_{2,dd}e^{4\sigma }$$

$$i_{2,uu}=i_{2,du}e^{2\sigma }$$

$$i_{2,du}=i_{2,dd}e^{2\sigma }$$

Example: Binomial Interest Rate Tree

To calibrate a binomial interest rate tree, a portfolio manager collects the following information relating to the spot rate curve and forward rates:

$$ \begin{array}{c|c} \textbf{Term to Maturity} & \textbf{Spot Rate} \\ \hline 1 & 4.00\% \\ \hline 2 & 5.00\% \\ \hline 3 & 6.00\% \end{array} $$

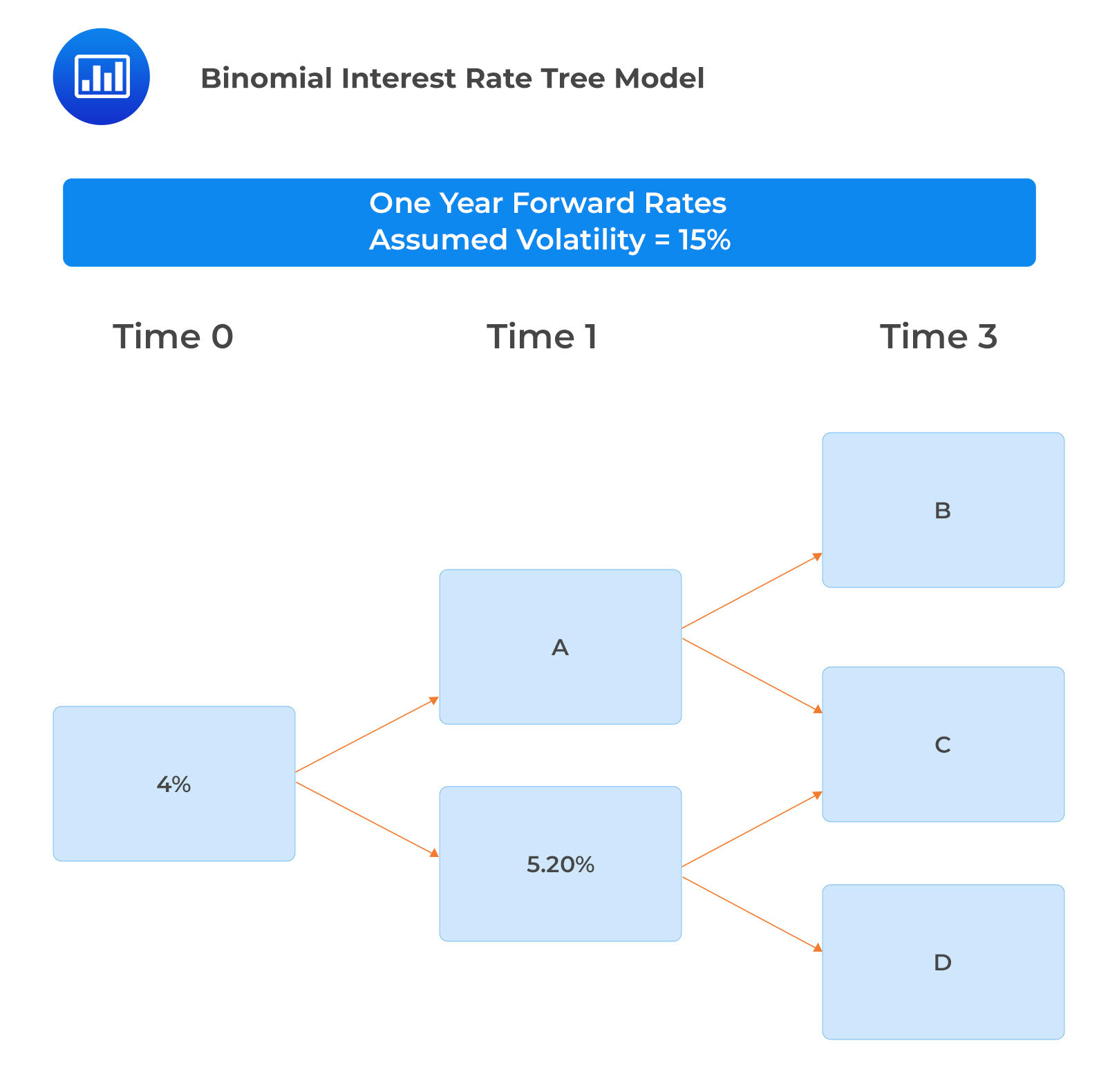Determine the forward rates A, B, C, and D.

Forward rate A

$$ \begin{align*} \text{The higher rate is determined as } i_{1u}&=i_{1d}\times e^{2\sigma} \\ &=5.20\%\times e^{2\times0.15}=7.019\%  \end{align*} $$

Forward rate C

This is the middle forward rate approximated as \(f (2,1)\). Recall from the previous reading the relationship between forward and spot rates:

$$ \begin{align*} \left[1+f\left(t,T-t\right)\right]^{T-t} &=\left[\frac{\left(1+S_T\right)^T}{\left(1+S_t\right)^t}\right] \\ (1+f\left(2,1\right) &=\left[\frac{\left(1+S_3\right)^3}{\left(1+S_2\right)^2}\right] \\ f\left(2,1\right) &=\frac{{1.06}^3}{{1.05}^2}-1=8.029\% \end{align*} $$

Forward rate B

$$ \begin{align*} i_{2,uu} &=i_{2du } e^{2\sigma} \\ i_{2,uu} &=8.029\%\times e^{2\times0.15 }=10.84\% \end{align*} $$

Forward rate D

$$ \begin{align*} i_{2,dd} &=i_{2du} e^{-2\sigma} \\ i_{2,dd} &=8.029\%\times e^{-2\times0.15 }=5.95\% \end{align*} $$

It is key to note that the change in the volatility assumption affects implied forward rates. A change of volatility to a lower value makes the potential implied forward rates to collapse on the tree and vice versa.

Question

Chen Cheng, a portfolio manager at ABC Investment Bank, is training Zhang Wang, a junior investment analyst, on calibrating binomial interest rate models using Excel. Cheng starts the process by guessing a lower one-year forward rate, \(i_{1,d}\), of 3.820%. Assuming that Cheng uses a volatility assumption of 20%, the higher one-year forward rate using the lognormal model of interest rates is closest to:

1. 2.56%.
2. 4.67%.
3. 5.70%.

Solution

The correct answer is C.

Based on the lognormal model of interest rates, the higher one-year forward rate is \((i_{1,u})=i_{1,d}e^{2\sigma}\).

$$ \begin{align*} i_{1,d} &=3.820\% \\ (i_{1,u}) &=3.820\%\times e^{2\times0.20}=5.70\%  \end{align*} $$

Reading 29: The Arbitrage-Free Valuation Framework

LOS 29 (d) Describe the process of calibrating a binomial interest rate tree to match a specific term structure.