Backward Induction

Backward induction involves working backward from maturity to time 0 to determine a bond’s value at each node. It makes the following assumptions:

1. The value of a bond is known at maturity (Final coupon payment + Face value).
2. The value at each node is the expected present value of two possible values from the next period.
3. The discount rate is the forward rate for that node.

Formula: Bond Value at a Node

$$V=0.5\left[\frac{V_u+C}{1+i}+\frac{V_d+C}{1+i}\right] $$

Where:

• \(V_u\) and \(V_d\) are the bond values if the higher and lower forward rates, respectively, are realized in one year.
• \(i\) is the forward interest rate at a particular node.
• \(C\) is the coupon rate, that is independent of interest rates.

Example: Backward Induction

A two-year bond with no embedded options pays 8% annual coupons. Given the following interest rate tree, find the values of the bond at each node, i.e., \(V_{1,u},\) \(V_{1,d}\) and \(V_0\).

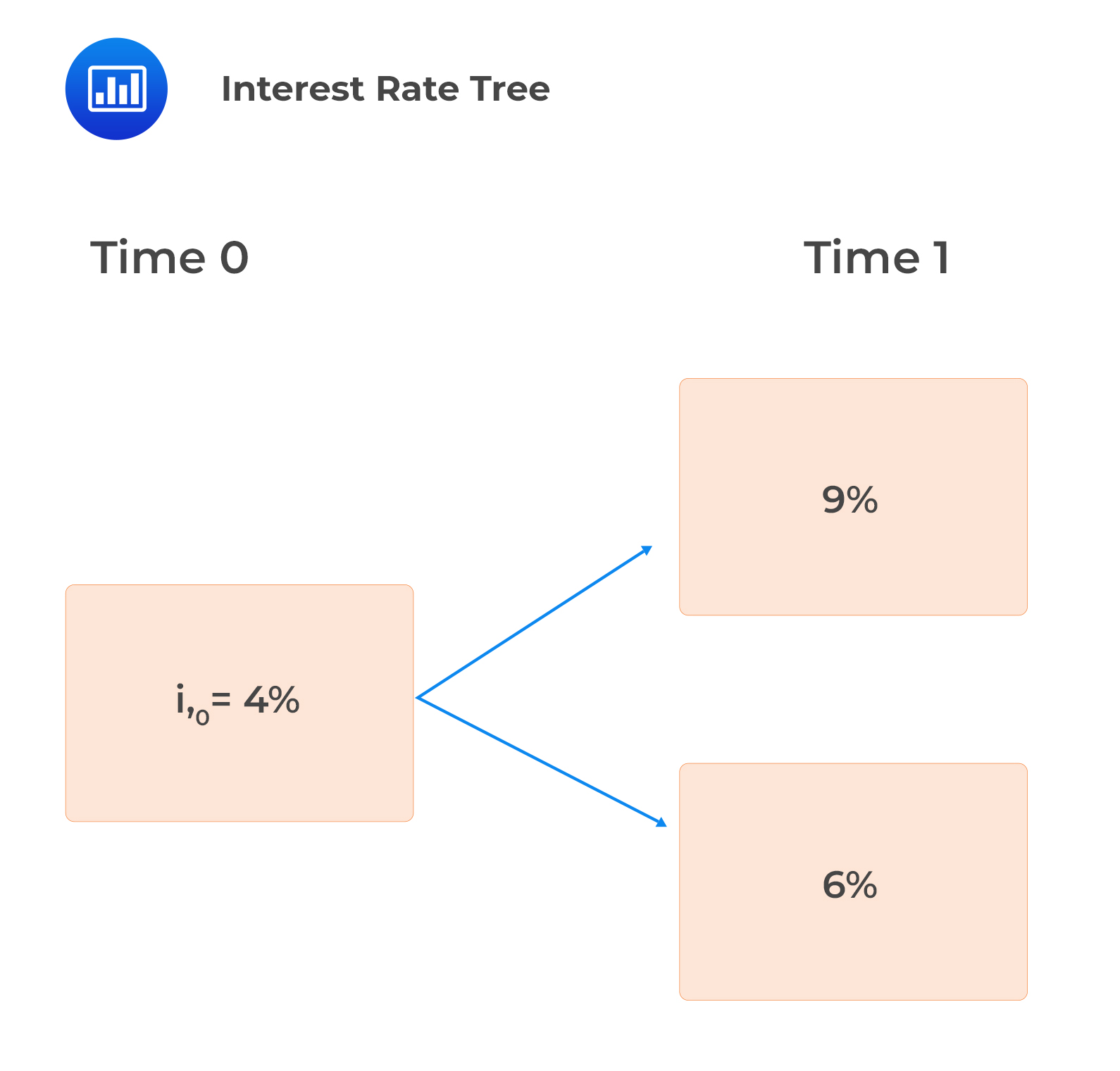Solution

$$ \begin{align*} V_{1,u} &=0.5\times\left[\frac{100+8}{1.09}+\frac{100+8}{1.09}\right]=$99.08 \\ V_{1,d}& =0.5\times\left[\frac{100+8}{1.06}+\frac{100+8}{1.06}\right]=$101.89 \text{ and}\\ V_0 &=0.5\times\left[\frac{99.08+8}{1.04}+\frac{101.89+8}{1.04}\right]=$104.31 \end{align*} $$

The resulting interest rate tree is as shown below:

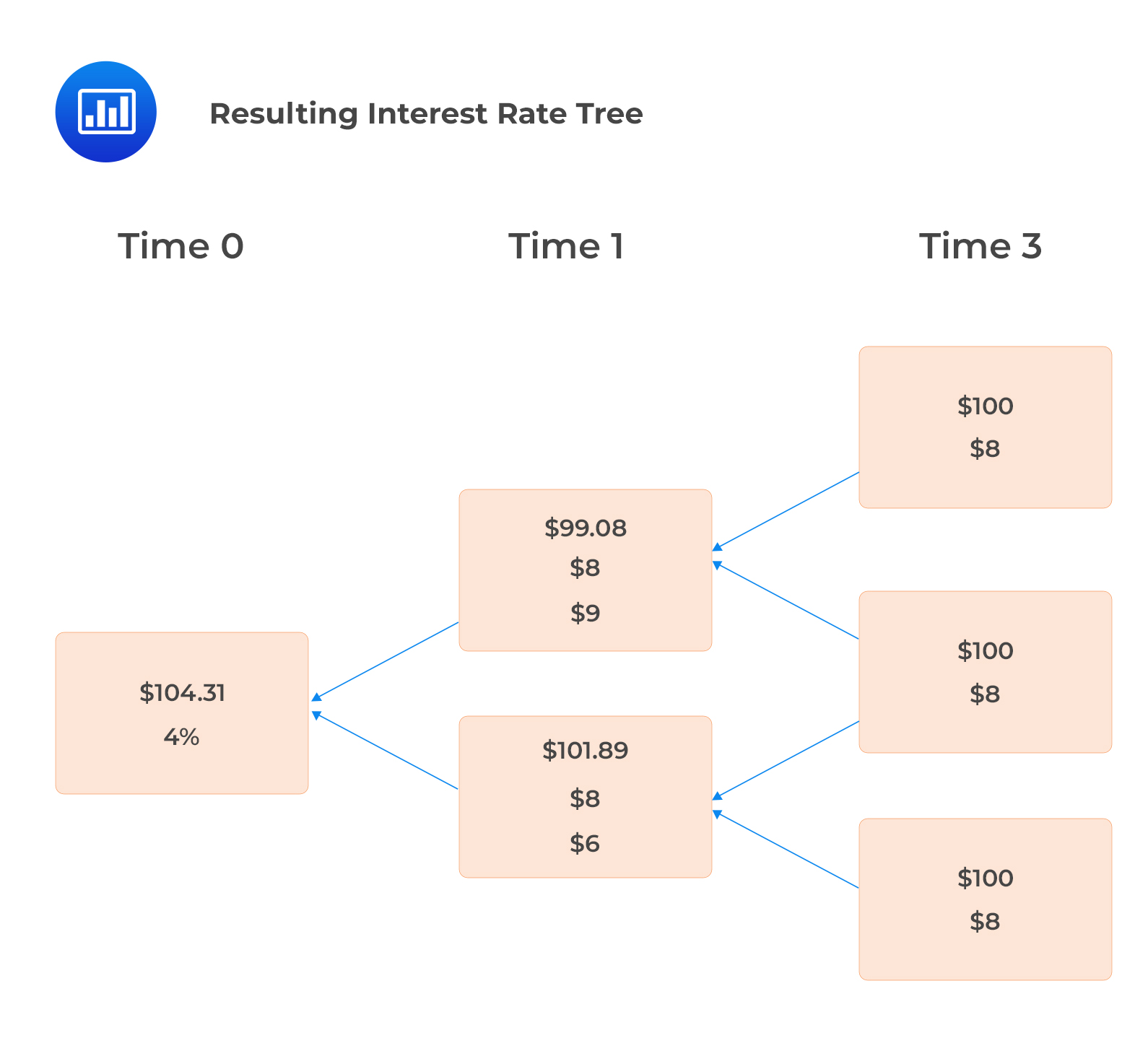
Question

Exhibit 1 is a binomial interest rate tree related to a bond with annual coupons of 4% with a face value of $100 that matures in three years.

Based on Exhibit 1, the price of the bond is closest to:

1. $101.90.
2. $103.87.
3. $105.51.

Solution

The correct answer is C.

$$ V=0.5\left[\frac{V_u+C}{1+i}+\frac{V_d+C}{1+i}\right] $$

The cash flow at Time 3 is 104, the redemption of par value ($100) plus the final coupon payment ($4)

Node values for time two are determined as follows:

$$ \begin{align*} & \text{Upper node: }\frac{104}{1.03}=100.97 \\ & \text{Middle node: }\frac{104}{1.02}= 101.96 \\ & \text{Lower node: }\frac{104}{1.01}= 102.97 \end{align*} $$

Time 1

$$ \begin{align*} & \text{Upper node: } 0.5\times\left(\frac{100.97+4}{1.035}+\frac{101.96+4}{1.035}\right)= 101.90 \\ & \text{Lower node: } 0.5\times\left(\frac{101.96+4}{1.025}+\frac{102.97+4}{1.025}\right)= 103.87 \end{align*} $$

Time 0

$$ \text{Node value: } 0.5\times\left(\frac{101.90+4}{1.013}+\frac{103.87+4}{1.013}\right)= 105.51 $$

Therefore, the price of the bond is $105.51.

This can be shown in the interest rate tree framework.

Reading 29: The Arbitrage-Free Valuation Framework

LOS 29 (e) Describe the backward induction valuation methodology and calculate the value of a fixed-income instrument given its cash flow at each node.