Binomial Interest Rate Model

Modeled future interest rates can take on different possible values, depending on the level of volatility assumed. This can be shown using an interest rate tree framework. One of the most popular tools used is the binomial interest rate model. It is so named because it assumes the short interest rate can only take on one of two possible values on a given future date.

The binomial interest rate tree represents the possible values of short interest rates consistent with an interest rate model and a volatility assumption. This model is built using one-year spot rate and one year forward rates including, \(f(1,1)\) \(f(2,1)\), \(f(3,1)\), and so on. The binomial interest rate tree represents possible paths and assumes an equal probability of upward or downward interest rate movements.

The binomial interest rate tree model is a lognormal random walk with the following properties:

• Interest rates are strictly positive.
• There is higher volatility at higher interest rates.
• Adjacent forward rates on the tree are multiples of \(e^{2\sigma}\).

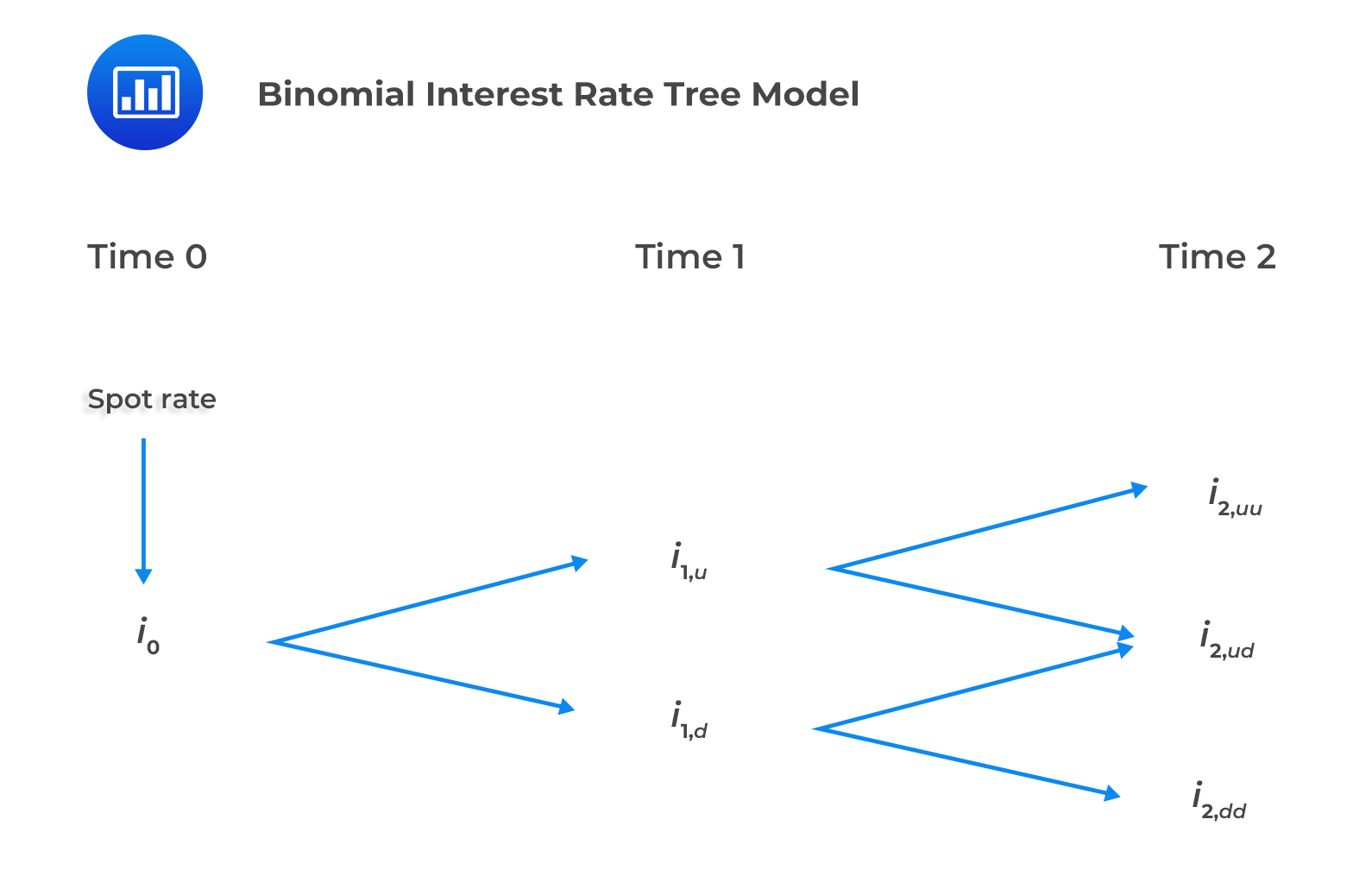Note to candidates: Nodal values represent the forward interest rates.

The interest rate volatility assumed in the binomial interest rate tree model can be estimated using two methods:

• Historical approach: Data from the recent past is used to estimate historical interest rate volatility. It is assumed that the recent past indicates the future.
• Implied volatility approach: Observed market price data of interest rate derivatives is used to estimate the implied volatility. 

Question

Which of the following is most likely a property of the binomial interest rate tree model?

1. Non-negative interest rates.
2. Higher volatility at higher interest rates.
3. Negative interest rates.

Solution

The correct answer is B.

The binomial interest rate tree model is a lognormal model characterized by non-negative interest rates and higher volatility at higher interest rates.

Reading 29: The Arbitrage-Free Valuation Framework

LOS 29 (c) Describe a binomial interest rate tree framework.