Capped or Floored Floating-Rate Bonds

Capped and floored floaters can be valued using the arbitrage-free framework.

Valuation of a Capped Floater

A capped floater (floating rate loan) is a bond that pays a coupon that resets every period based on the reference rate. Reference rates can be EURIBOR or LIBOR.

The coupon is determined at the beginning of each period and is paid at the end of each period.

Thus, a capped floater protects the issuer against rising interest rates above a certain maximum rate. This makes it an issuer option.

$$ \text{Value of capped floater} = \text{Value of straight bond}  – \text{Value of embedded cap} $$

Example: Capped Floater

A three-year floating rate bond pays annual coupons of one-year Euribor at the end of each year and is capped at 6.00%. The Euribor swap curve is given in the binomial lattice below. The interest rate volatility is assumed to be 15%.

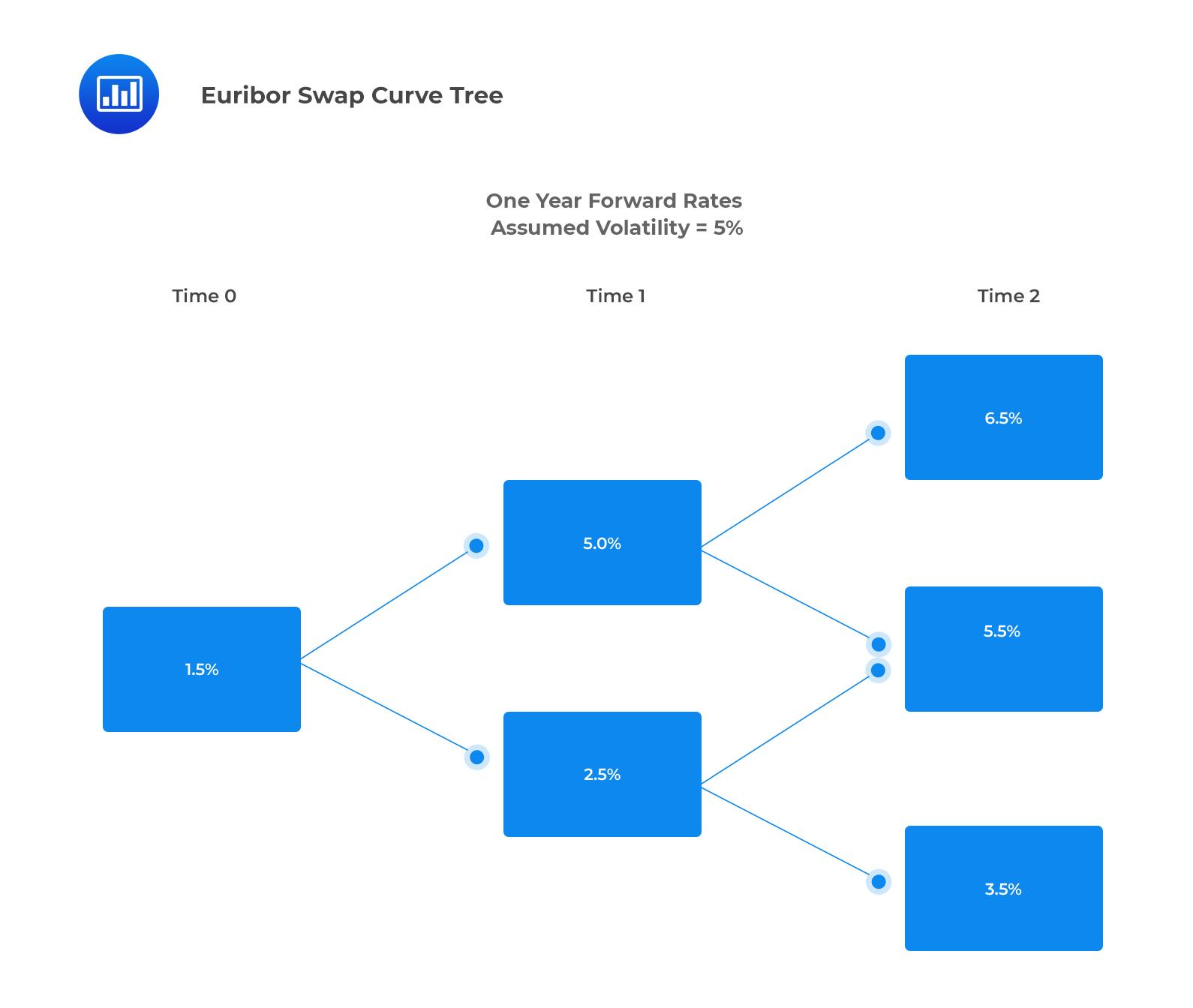The value of the capped floater and embedded cap are closest to:

Solution

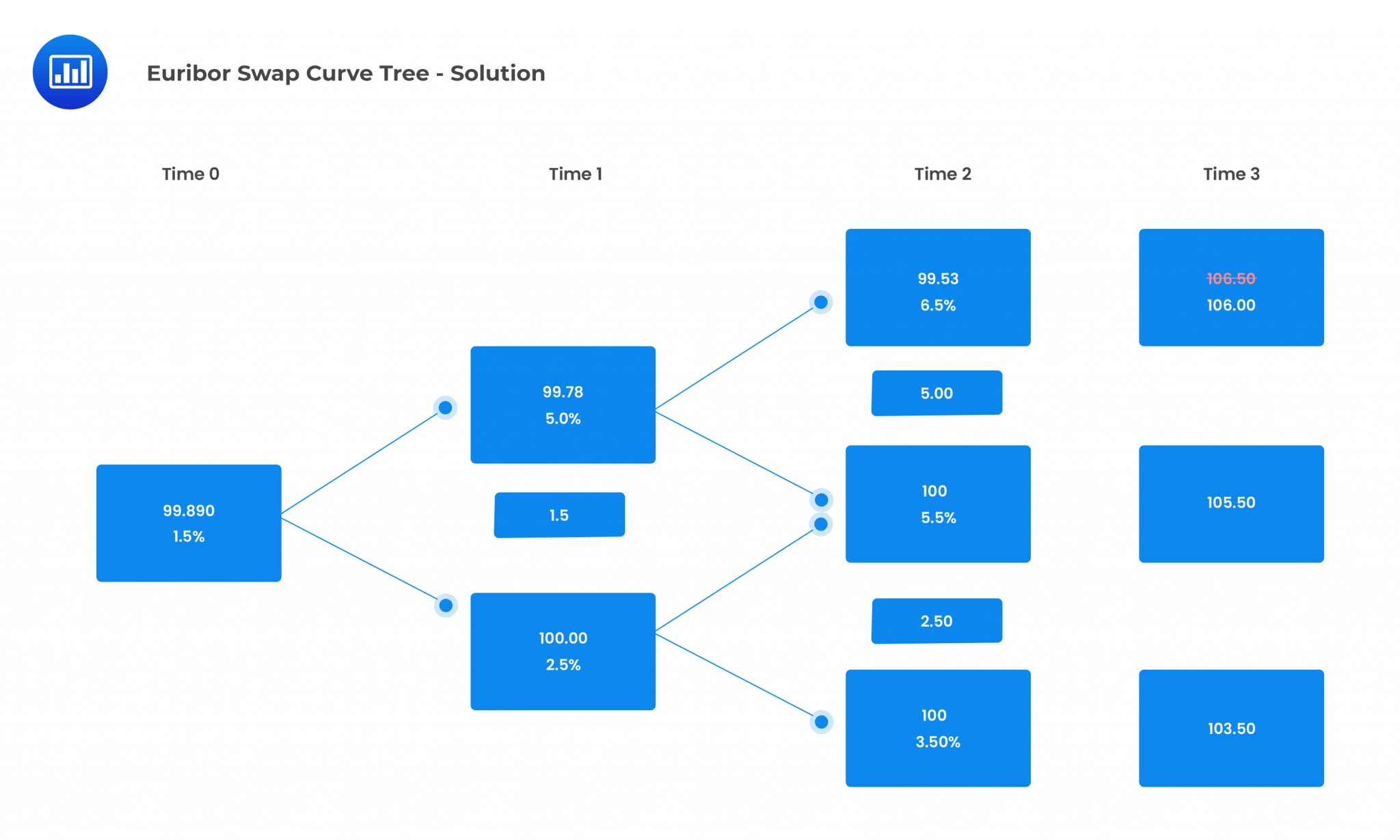Therefore, the value of the capped floater is 99.89.

$$ \text{Value of embedded cap} = 100-99.89 = 0.11 $$

Valuation of a Floored Floater

A floored floater is a floating rate bond whose coupon rate cannot fall below a specified minimum rate, which is known as the floor.

The investor is long an embedded option that offers protection against falling interest rates. Thus, it is referred to as an investor option.

$$ \text{Value floored floater} = \text{Value of straight bond}  + \text{Value of embedded floor} $$

Example: Floored Floater

A three-year floating rate bond pays annual coupons of one-year Euribor at the end of each year and is floored at 2.0%. The Euribor swap curve is given in the interest rate tree below. The interest rate volatility is assumed to be 15%.

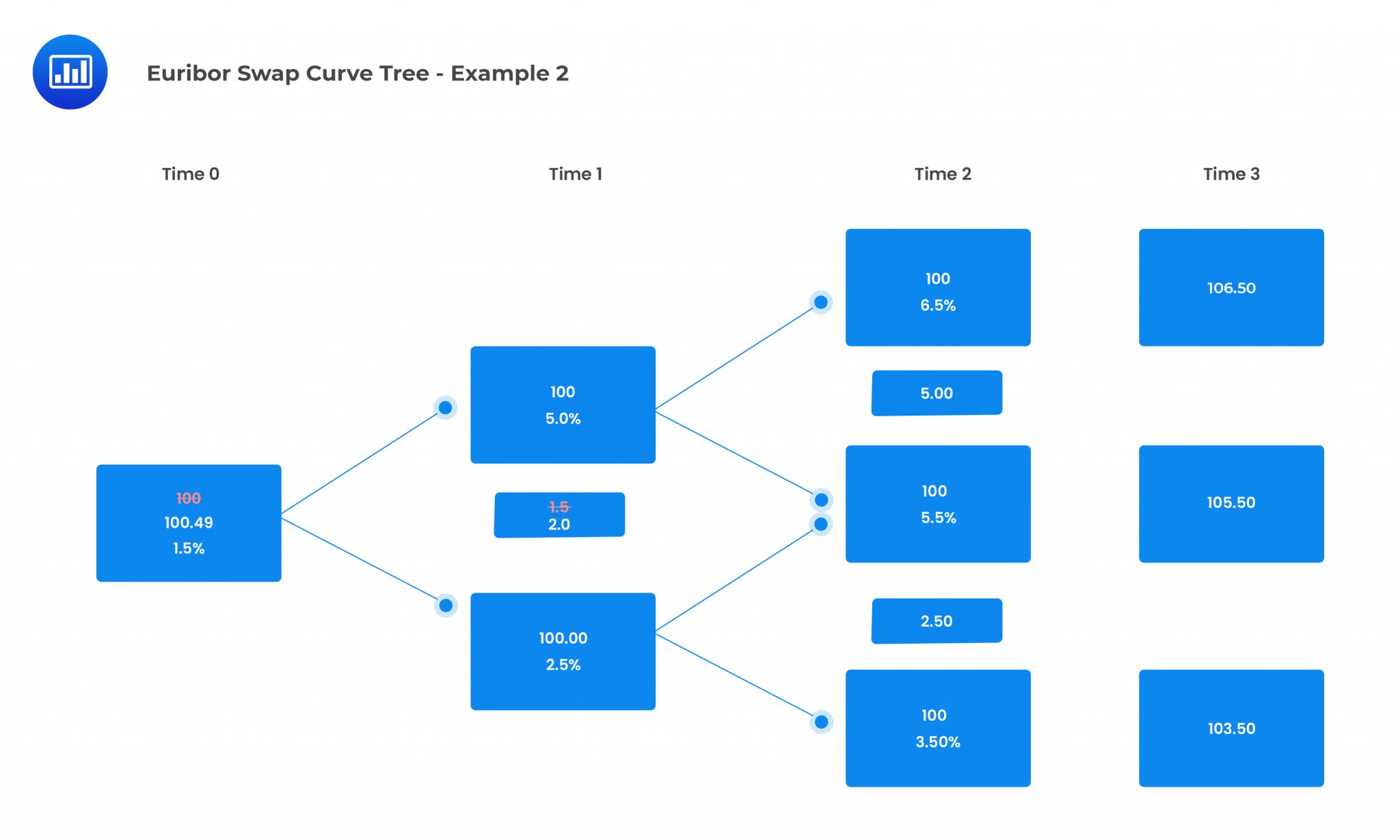The value of the floored floater is closest to:

Solution

From the above binomial tree, the value of the floored floater has been calculated to be $100.49.

The floor adds 0.49 in value to the straight bond. Had the floor been 1.5%, the floored floater and the straight bond would be worth par.

Question

A three-year floating rate bond pays coupons of one-year LIBOR annually, set in arrears and capped at 5%. The Libor swap curve is as given in the binomial lattice below. The interest rate volatility is assumed to be 10%.

The value of the capped floater is closest to:

1. 99.44.
2. 99.77.
3. 100.00.

Solution

The correct aswer is A.

Reading 30: Valuation and Analysis of Bonds with Embedded Options

LOS 30 (m) Calculate the value of a capped or floored floating-rate bond.