Valuing Bonds with Embedded Options

The steps for valuing a bond with an embedded option in the presence of interest rate volatility are as follows:

Step 1: Generate an interest rate tree using the yield curve and interest rate volatility assumptions.

Step 2: Determine whether the embedded option will be exercised at each node.

Step 3: Calculate the present value of the bond using the backward induction method.

Recall that backward induction involves starting from maturity and working backward from right to left to determine the bond’s value at each node.

Example: Valuation of Bonds with Embedded Options Assuming Interest Rate Volatility

The following interest rate tree has been calibrated, assuming a 15% interest rate volatility and the applicable benchmark yield curve.

We can determine the value of a three-year default-free 5% annual coupon bond, both callable and putable at par one year and two years from today.

Callable Bond

Formula:

$$ V=0.5\left[\frac{V_u+C}{1+i}+\frac{V_d+C}{1+i}\right] $$

Where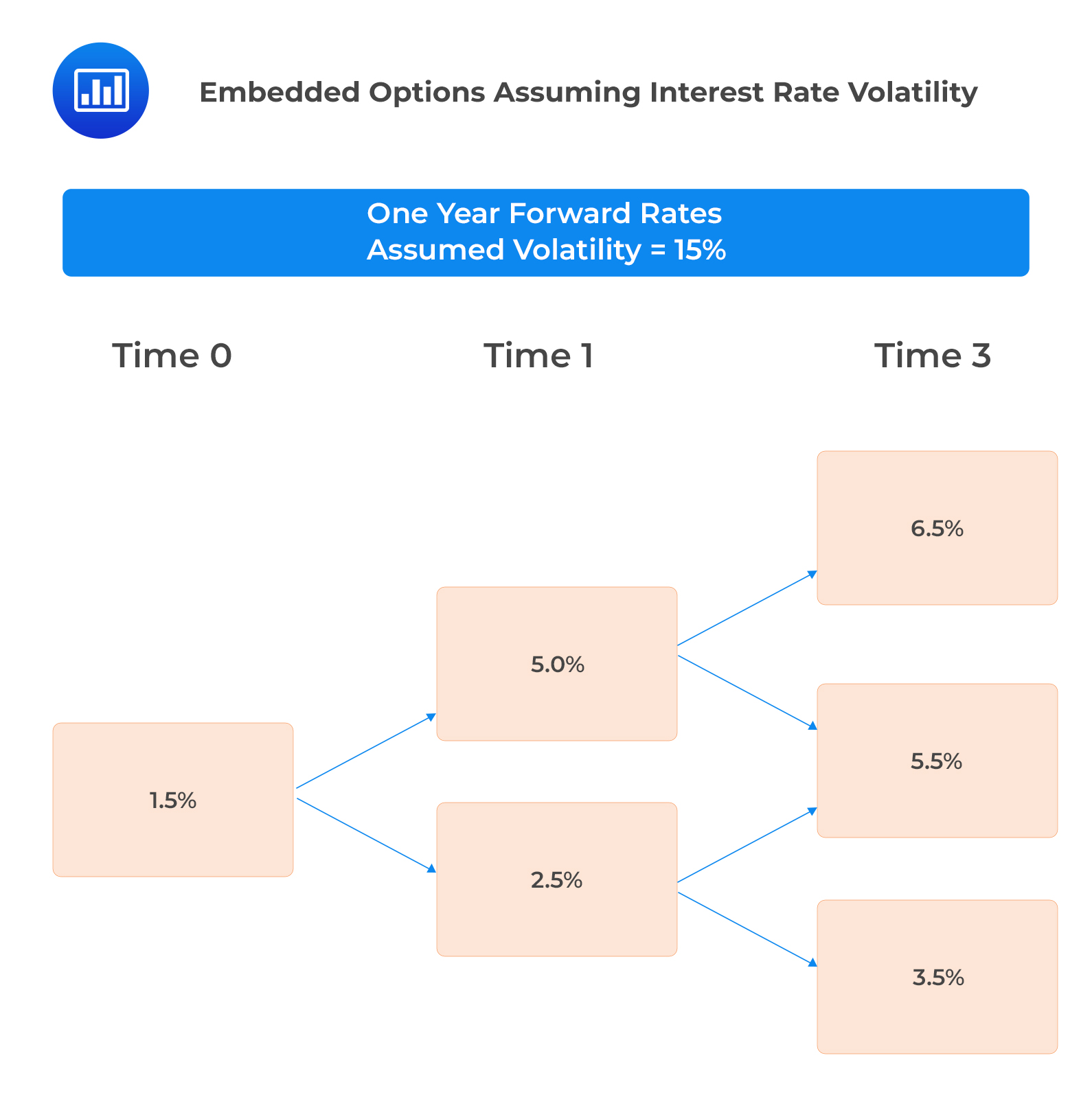

V = Value of the bond at each node.

C = Coupon payment.

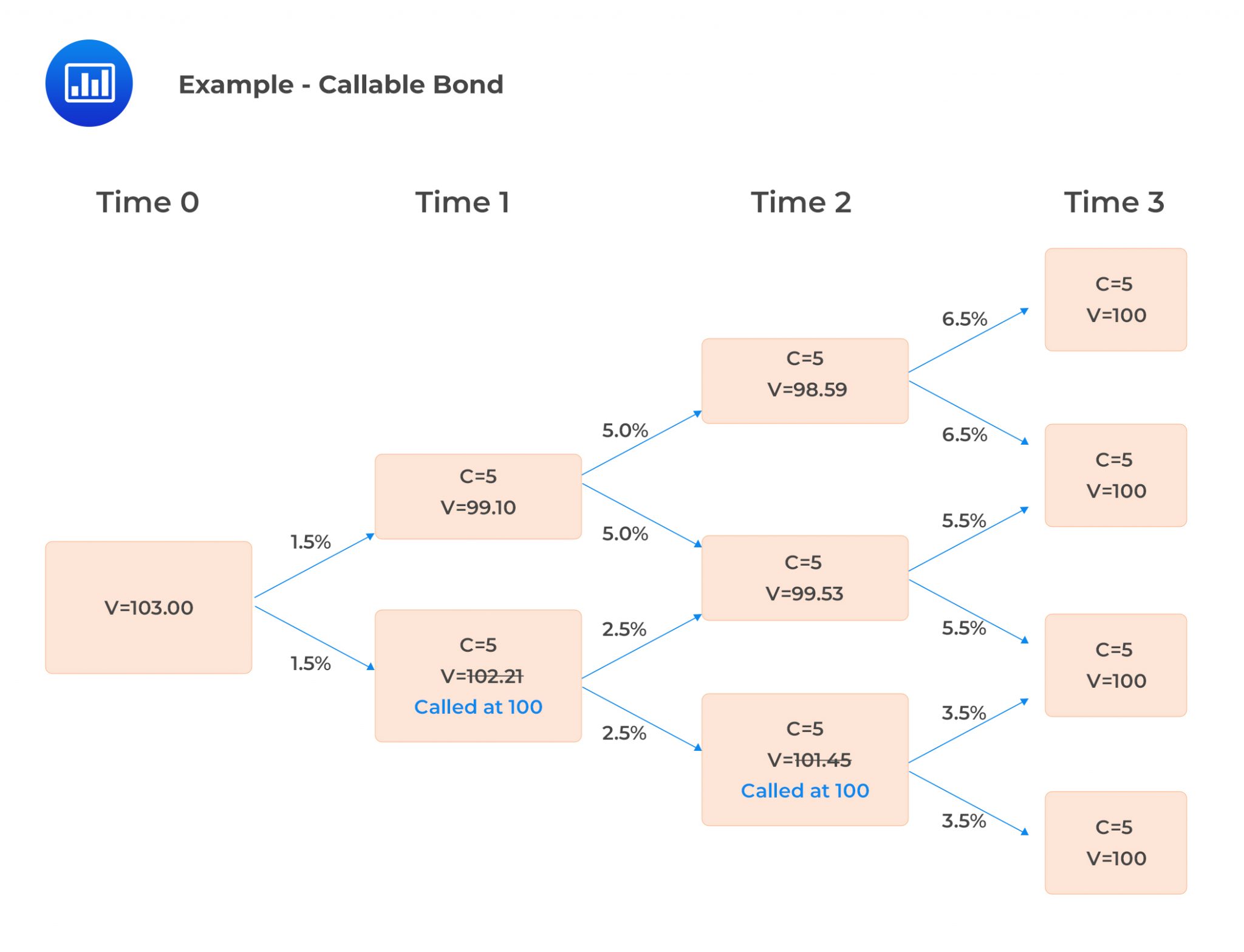
The bond value at each node must meet the call rule (call the bond if the price exceeds $100) for the option to be exercised.

$$ \begin{align*} V_{2,uu} &=\frac{105}{1.065}=98.59 \\ V_{2,ud} &=\frac{105}{1.055}=99.53 \\ V_{2,dd} &=\frac{105}{1.035}=101.45 \\ V_{2,dd} &= $101.45 > $100. \end{align*} $$

The bond will thus be called at $100. To continue with the valuation, the bond’s value at this node will be taken as $100.

$$ \begin{align*} V_{1,u} &=0.5\left[\frac{98.59+5}{1.05}+\frac{99.53+5}{1.05}\right]=$99.10 \\ V_{1,d} &=0.5\left[\frac{99.53+5}{1.025}+\frac{100+5}{1.025}\right]=$102.21 \end{align*} $$

\(V_{1,d} > $100,\) implying that the bond is called at $100.

$$ V_0 =0.5\left[\frac{99.10+5}{1.015}+\frac{100+5}{1.015}\right]=$103.00 $$

This can be shown in the following tree:

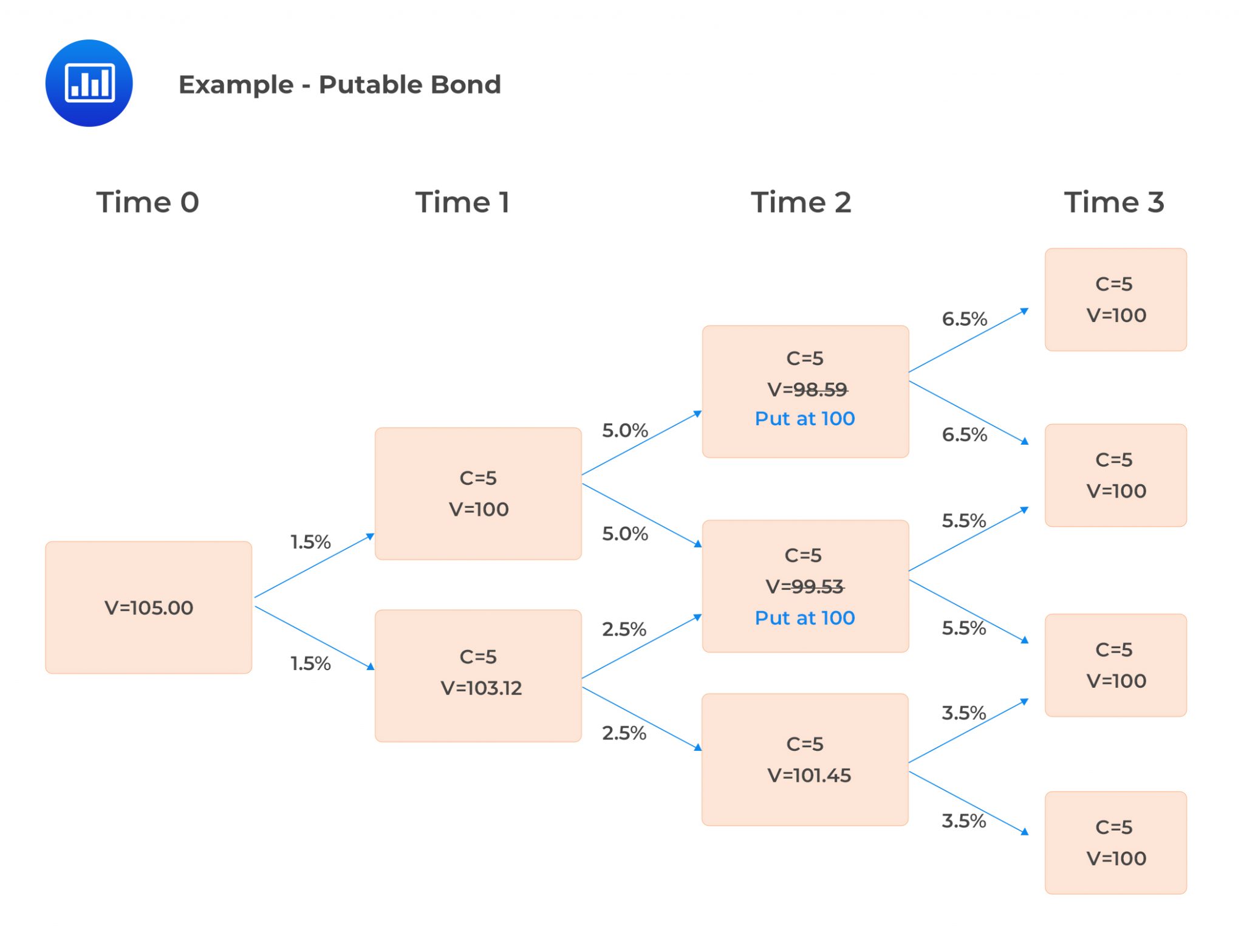
Putable Bond

The value of the bond at each node is calculated using the formula:

$$ V=0.5\left[\frac{V_u+C}{1+i}+\frac{V_d+C}{1+i}\right] $$

Further, the embedded put option will be exercised at each node of the tree if the value of the bond is less than $100. This is known as the put rule.

$$ \begin{align*} V_{2,uu} &=\frac{105}{1.065}=98.59 \\ V_{2,ud} &=\frac{105}{1.055}=99.53 \\ V_{2,dd} &=\frac{105}{1.035}=101.45 \end{align*} $$

Notice that both \(V_{2,uu}\) and \(V_{2,ud}\) are less than $100. In this case, the bond will be put at $100. To continue with the valuation, the values of the bond at these nodes will be taken as $100.

$$ \begin{align*} v_{1,u} & =0.5\left[\frac{100+5}{1.05}+\frac{100+5}{1.05}\right]=$100\\ v_{1,d} & =0.5\left[\frac{100+5}{1.025}+\frac{101.45+5}{1.025}\right]=$103.12 \\ v_0 &=0.5\left[\frac{100+5}{1.015}+\frac{103.12+5}{1.015}\right]=$105.00 \end{align*} $$

This can be shown in the following tree:

Question

Given the following interest rate tree:

The value of a two-year,6% annual coupon bond, with a par value of $100 and callable at par at the end of year 1 is closest to:

1. $101.30.
2. $101.53.
3. $102.64.

Solution

The correct answer is A.

The value of the bond at each node is calculated using the formula:

$$ V=0.5\left[\frac{V_u+C}{1+i}+\frac{V_d+C}{1+i}\right] $$

The call rule will then be used to establish if the embedded call option will be exercised at each node.

$$ \begin{align*} v_{1,u} &=0.5\left[\frac{100+6}{1.085}+\frac{100+6}{1.085}\right]=$97.696 \\ v_{1,d} &=0.5\left[\frac{100+6}{1.055}+\frac{100+6}{1.055}\right]=$100.474 \end{align*} $$

\(v_{1,d}>$100\). Therefore, the bond is called at $100.

$$ v_0=0.5\left[\frac{97.696+6}{1.035}+\frac{100+6}{1.035}\right]=$101.30 $$

Reading 30: Valuation and Analysis of Bonds with Embedded Options

LOS 30 (f) Calculate the value of a callable or putable bond from an interest rate tree.