Risk Measures and Capital Allocation
Capital allocation is critical to a firm’s market risk management. It involves setting... Read More
Heteroskedasticity is the dependence of the variance of the error term on the independent variable. We have been assuming that time series follows the homoskedasticity assumption. Homoskedasticity is the independence of the variance of the error term on the independent variable. Violation of this condition leads to heteroskedasticity.
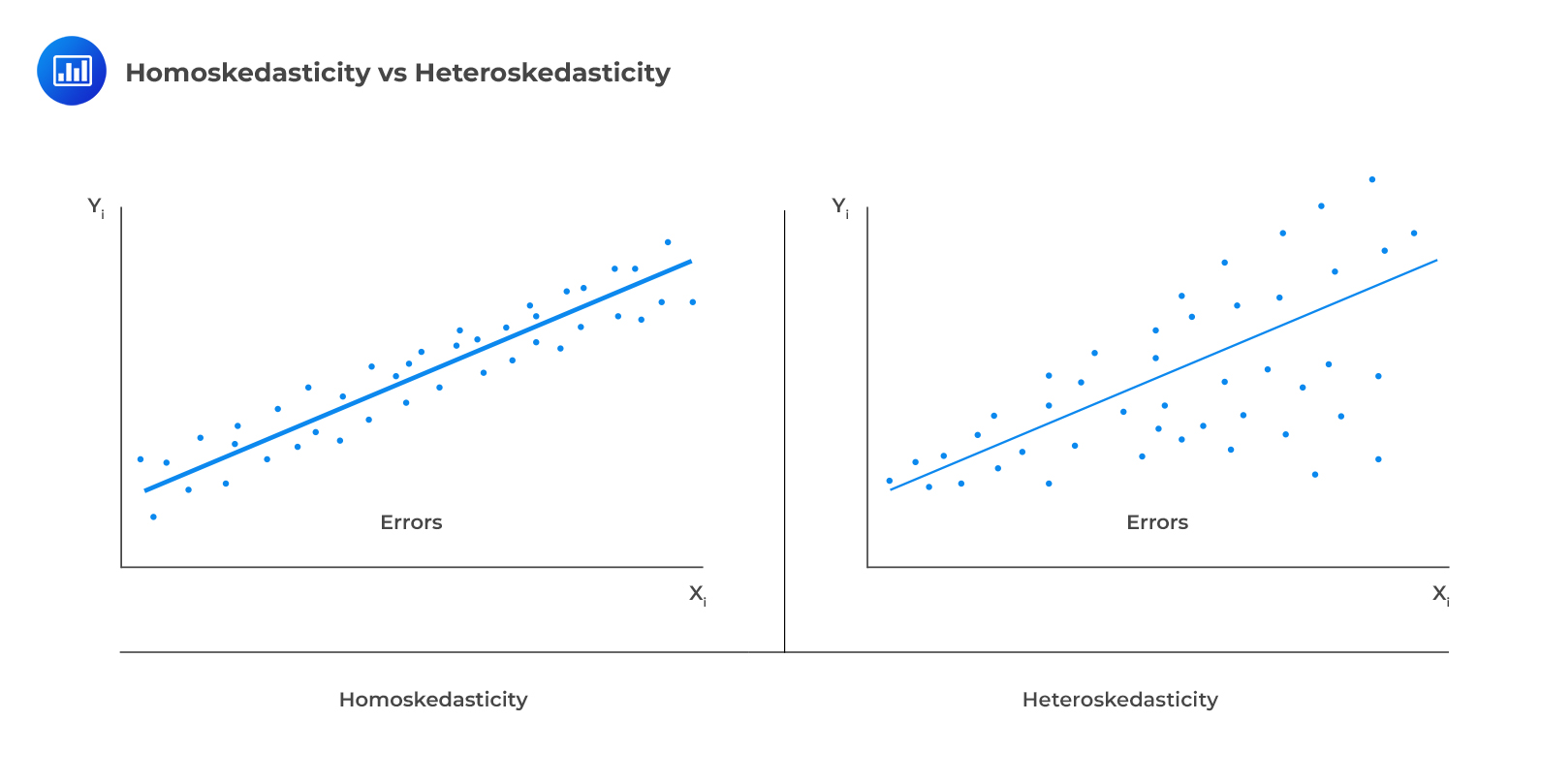 Heteroskedasticity in the autoregressive model makes the standard errors of the regression coefficients of the model invalid, leading to misleading interpretations.
Heteroskedasticity in the autoregressive model makes the standard errors of the regression coefficients of the model invalid, leading to misleading interpretations.
Autoregressive conditional heteroskedasticity is a problem associated with the correlation of variances of the error terms. An ARCH(1) model is an AR(1) model with conditional heteroskedasticity.
The error terms in an ARCH(1) model are normally distributed with a mean of 0 and a variance of \(\text{a}_{0}+\text{a}_{1}\epsilon_{\text{t}-1}^{2}\).
$$\epsilon_{\text{t}}∼\text{N}(0, \text{a}_{0}+\text{a}_{1}\epsilon_{\text{t}-1}^{2})$$
Steps for Testing for ARCH(1) Conditional Heteroskedasticity
Given an ARCH(1) model, we can use the parameter estimates from our test for conditional heteroskedasticity to predict next period variance as:
$$\hat{\sigma}_{\text{t}+1}^{2}=\hat{\alpha}_{0}+\hat{\alpha}_{1}\hat{\epsilon}_{\text{t}}^{2}$$
The following results have been obtained from regressing the squared residuals of an estimated autoregressive model on a constant and one lag of the squared error terms.
$$\small{\begin{array}{c|c} \text{R-squared} & 0.0430 \\ \hline\text{Standard error} & 24.638 \\ \hline\text{Observations} & 358 \\ \text{Durbin-Watson} & 2.1021\\ \hline\end{array}}$$
$$\small{\begin{array}{c|c|c|c} {}&\textbf{Coefficient}&\textbf{Standard Error}&\textbf{t-Statistic}\\ \hline\text{Intercept}&9.1680&1.4104&6.55002\\ \hline \hat{\epsilon}_{\text{t}-1}^{2}&0.2050&0.0506&4.0514\\ \end{array}}$$
Solution
The test involves the first lag of the residuals of the approximated time series model, and thus the number of the observations is less by one. The number of degrees of freedom is \(358-1=357\), and the corresponding critical t-value at the 5% level of significance is 1.97.
The t-statistic on \(\hat{\epsilon}_{\text{t}-1}^{2}\) is greater than the critical value. This implies that \(\hat{\alpha}_{1}\) is statistically significantly different from 0. Therefore, the time series has ARCH(1) errors.
The predicted variance for the next period is determined using the formula:
$$\hat{\sigma}_{\text{t}}^{2}=\hat{\alpha}_{0}+\hat{\alpha}_{1}\hat{\epsilon}_{\text{t}-1}^{2}$$
$$\hat{\sigma}_{\text{t}}^{2}=9.1680+0.2050\hat{\epsilon}_{\text{t}-1}^{2}$$
So that the variance for the next period, in this case, is:
$$\hat{\sigma}_{\text{t}}^{2}=9.1680+0.2050\times0.005=9.169025$$
Question
Consider the following regression results for an ARCH(1) model:
$$\small{\begin{array}{c|c|c} {}&\textbf{Coefficients} & \textbf{P-value} \\ \hline\text{Constant} & 4.8347 & <0.001 \\ \hline\text{Lag 1} & 0.2678 & <0.001\\ \end{array}}$$
Given that the current period squared error is 0.678, the predicted variance of the error terms in the next period is closest to:
- 4.835.
- 5.103.
- 5.016.
Solution
The correct answer is C.
The predicted variance for the next period is determined using the formula:
$$\hat{\sigma}_{\text{t}}^{2}=\hat{\alpha}_{0}+\hat{\alpha}_{1}\hat{\epsilon}_{\text{t}-1}^{2}$$
$$\hat{\sigma}_{\text{t}}^{2}=4.8347+0.2678\times0.678=5.016$$
Reading 5: Time Series Analysis
LOS 5 (m) Explain autoregressive conditional heteroskedasticity (ARCH) and describe how ARCH models can be applied to predict the variance of a time series.
Get Ahead on Your Study Prep This Cyber Monday! Save 35% on all CFA® and FRM® Unlimited Packages. Use code CYBERMONDAY at checkout. Offer ends Dec 1st.