Assumptions of the Simple Linear Regression Model

Before we can draw conclusions, we need to make the following key assumptions.

1. Linearity: A linear relationship exists between the dependent variable, Y, and independent variable X.
2. Homoskedasticity: For all observations, the variance of the regression residuals is the same.
3. Independence: The observation X and Y pairs are independent of one another.
4. Normality: A normal distribution exists among regression residuals.

Let us discuss the assumptions in detail below.

Assumption 1: Linearity.

When fitting a linear model, we first assume that the relationship between the independent and dependent variables is linear. If the relationship between the two variables is non-linear, it will produce erroneous results because the model will underestimate or overestimate the dependent variable at certain points. Another implication of this assumption is that that X, the independent variable, should not be random because if it is random, there will be no linear relationship between the independent variable and the dependent variable.

As for the residuals of the model, they should be random and should not display a pattern when plotted against the independent variable.

$$E(ε_i^2 )=σ_ε^2,i=1,…,n.$$

Assumption 2: Homoskedasticity.

The homoskedasticity assumption states that for all observations, the variance of the residual is the same. This assumption relates to the squared residuals:

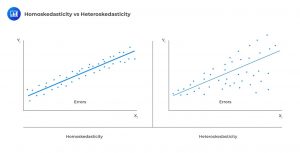
The opposite of homoskedasticity is heteroskedasticity, where all the observation of the variance residual is different. In some cases, we may plot the residuals, and the results will be different from the model, which is a clear violation of the homoskedasticity assumption.

Assumption 3: Independence.

While conducting a simple linear regression, we assume that the X and Y pairs of observation are not correlated, and the residuals will not be correlated. To ensure that the variances of the estimated parameters are correctly estimated, the assumption that the residuals are not correlated across the X and Y observation pairs is crucial. It is important to examine the residuals statistically and visually for a regression model to ensure that the residuals do not exhibit a pattern that suggests a violation of the assumptions.

Assumption 4: Normality

This assumption requires that the residuals from the model should be normally distributed. It is good practice for an analyst to understand the distribution of the independent and dependent variables to check for outliers that can affect the fitted line. When residuals are normally distributed, we can test a specific hypothesis about a linear regression model.

Question

An indication that the homoskedasticity assumption has been violated is likely to be?

1. All observations have the same variance of the residuals.
2. There is a difference in the variance of the residuals for all observations.
3. There is a correlation between the X and Y pairs of observations

Solution:

The correct answer is B. Homoskedasticity assumption is violated when the variance of the residuals for all observations is different.

A is incorrect. When the variance of the residuals is the same for all observations, there is no violation of the homoskedasticity assumption.

C is incorrect. This is a violation of the independence assumption.

Reading 0: Introduction to Linear Regression

LOS 0 (c) Explain the assumptions underlying the simple linear regression model and describe how residuals and residual plots indicate if these assumptions may have been violated