Electronic Trading Systems
The electronic trading system involves the use of modern information technologies in business.... Read More
A contingent claim is a derivative contract that gives the owner the right but not the obligation to receive a future payoff that depends on the value of the underlying asset. Call and put options are examples of contingent claims.
So far, the approaches we have used to price and value derivative contracts rest on the no-arbitrage principle. This principle states that prices adjust so as not to follow arbitrage profits.
The arbitrageur must follow the following two rules:
Rule 1: Do not use your own money.
Rule 2: Do not take any price risk.
The no-arbitrage valuation methodology applied in this reading is based on the law of one price. This law argues that two investments with comparable future cash flows have the same current price regardless of what happens in the future.
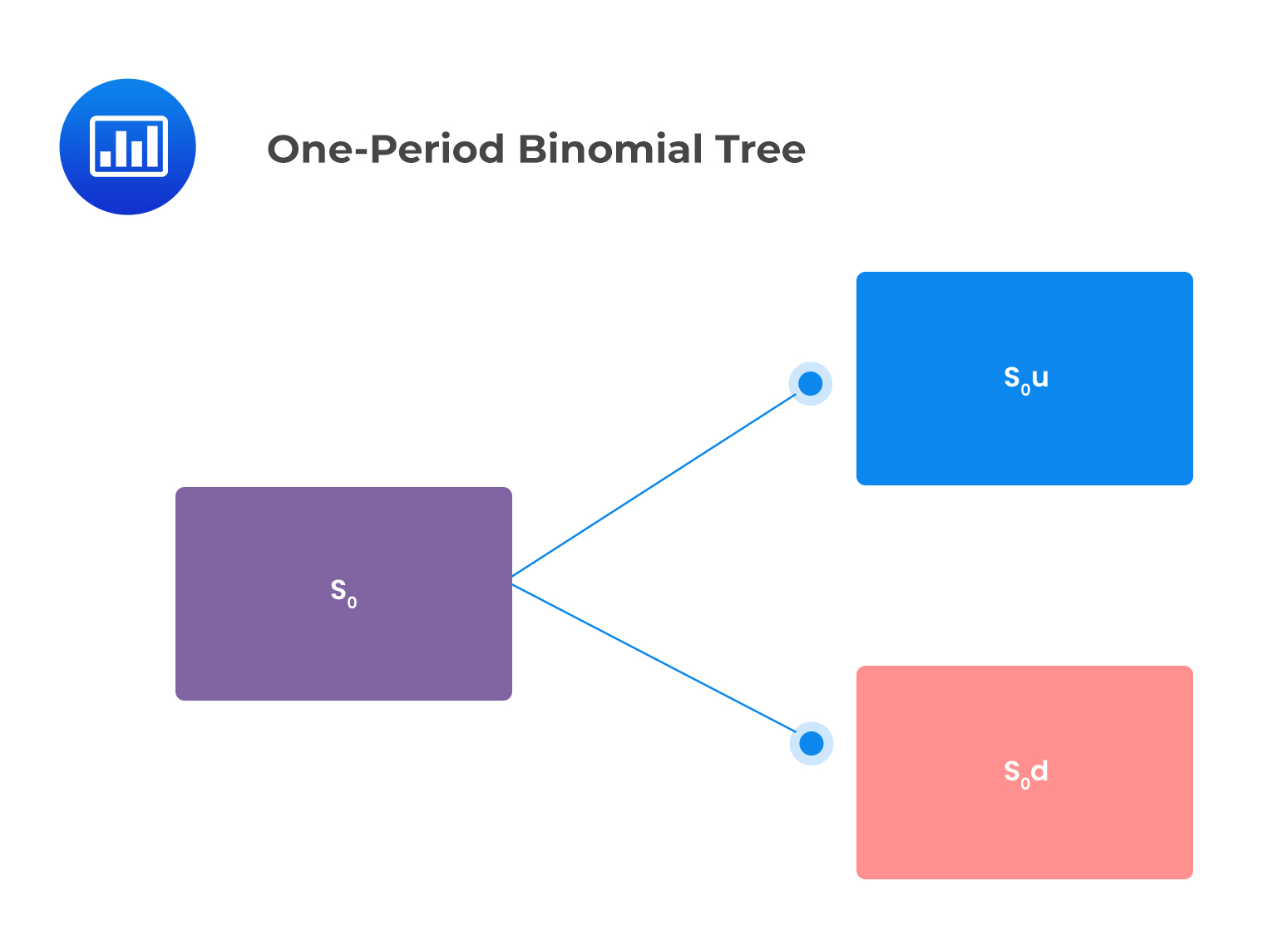
In the one-period binomial model, we start today (at time \(t = 0\)) when the stock price is \(S_0\). The stock price can then either jump upwards or downwards over the one-period time interval, to \(t=1\). This is illustrated below:
$$ S_1= {\left\{\begin{matrix} S_0u, & \text{if the stock price jumps up} \\ S_0d, & \text{if the stock price jumps down} \end{matrix}\right. } $$
This can be shown in the following binomial tree:
 Where:
Where:
$$ \begin{align*} u& =\frac{S_0u}{S_0} \\ d & =\frac{S_0d}{S_0} \end{align*} $$
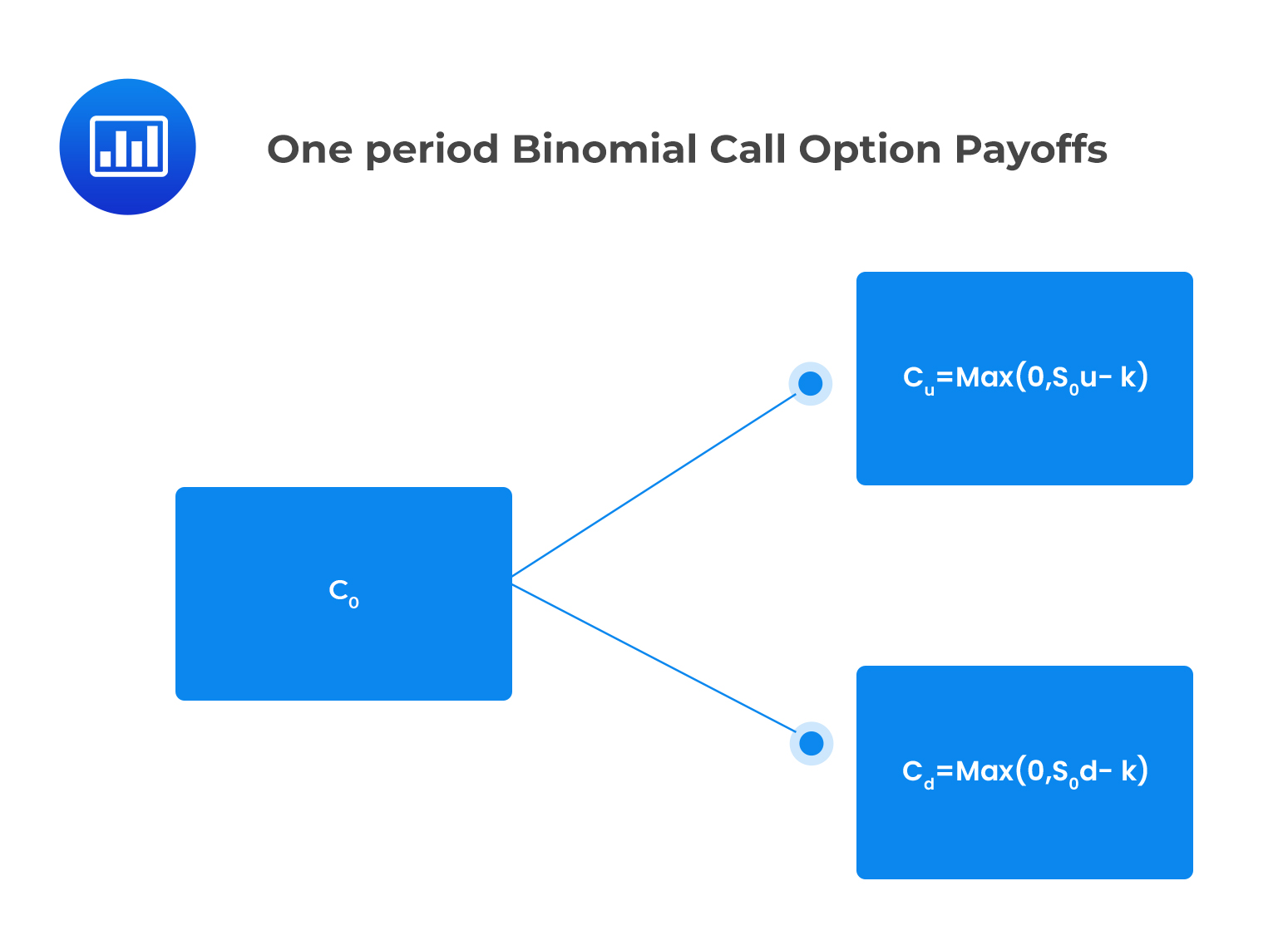
Consider a call option that pays \(c_u\) if the price of the underlying asset jumps up and \(c_d\) if the price of the underlying asset jumps down.
The value of the call option at expiry is expressed as:
\(c_u = Max\left(0,S_0u-K\right),\) if the price of the underlying jumps up
and
\(c_d = Max{\left(0,S_0d-K\right)},\) if the stock price jumps down
Where \(K\) is the strike price.
This is shown in the following binomial tree:
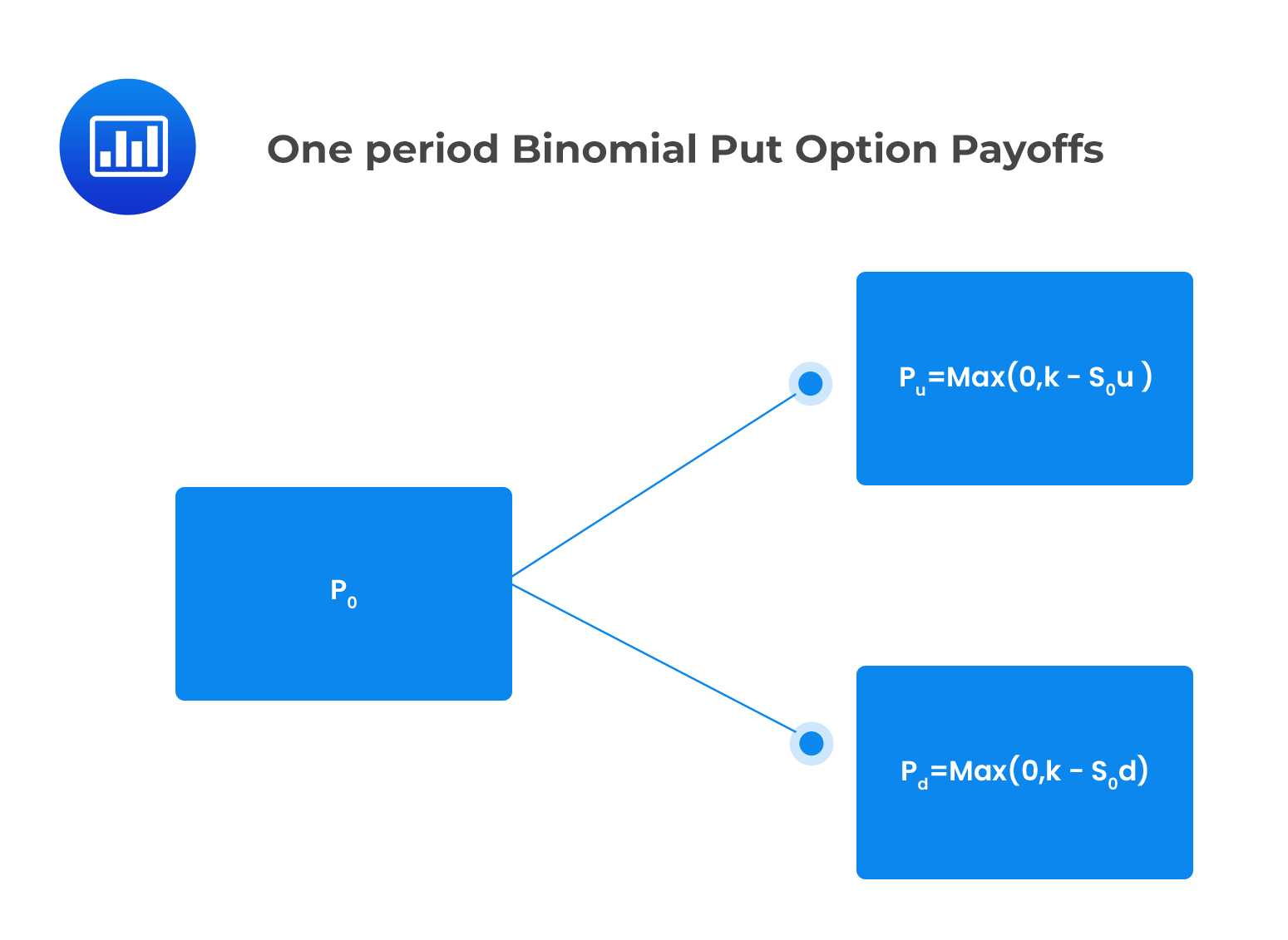
 Similarly, the value of a put option at expiration is given by:
Similarly, the value of a put option at expiration is given by:
\( p_u=Max\left(0, K-S_0u\right),\) if the price of the underlying asset jumps up $$
and
\(p_d=Max \left(0, K-S_Od \right)\) if the price of the underlying asset jumps down.
 One-period Binomial Option Values
One-period Binomial Option Values
The initial values of call and put options with a one period to expiry are determined using the following formulas:
$$ c_0=\frac{qc_u+\left(1-q\right)c_d}{1+r} $$
and
$$ p_0=\frac{qp_u+\left(1-q\right)p_d}{1+r} $$
Where:
$$ q=\frac{\left(1+r\right)-d}{u-d} $$
Where:
\(r\) is the risk-free rate for a single period.
\(q\) gives the risk-neutral probability of an upward move in price
\(1-q\) gives the risk-neutral probability of a downward move
Consider a European put option with a strike price of $50 on a stock whose initial price is $50. The risk-free rate of interest is 4%, the up-move factor u = 1.20, and the down move factor d = 0.83. The price of the put option can be determined using the one-period binomial model as follows:
$$ \begin{align*} S_0u& =50\times1.20=$60 \\ S_0d &= 50\times0.83=$41.50 \end{align*} $$
Recall that put payoff is given by:
\( p_u=Max\left(0, K-S_0u\right),\) if the price of the underlying asset jumps up
and
\(p_d=Max (0, K-S_Od)\) if the price of the underlying asset jumps down.
$$ \begin{align*} p_u &=Max\left(0,50-60\right)=$0 \\ p_d & =Max\left(0,60-41.50\right)=$18.50 \end{align*} $$
The value of the put is then calculated using the formula:
$$ p_0=\frac{qp_u+\left(1-q\right)p_d}{1+r} $$
Where:
$$ \begin{align*} q &=\frac{\left(1.04\right)-0.83}{1.20-0.83}=0.5676 \\ p_0 &=\frac{0.5676\times$0+0.4324\times$18.50}{1.04}=$7.69 \end{align*} $$
The one-period binomial model can be extended into a multi-period context. The two-period binomial lattice can be seen as three-one period binomial lattices as shown below:
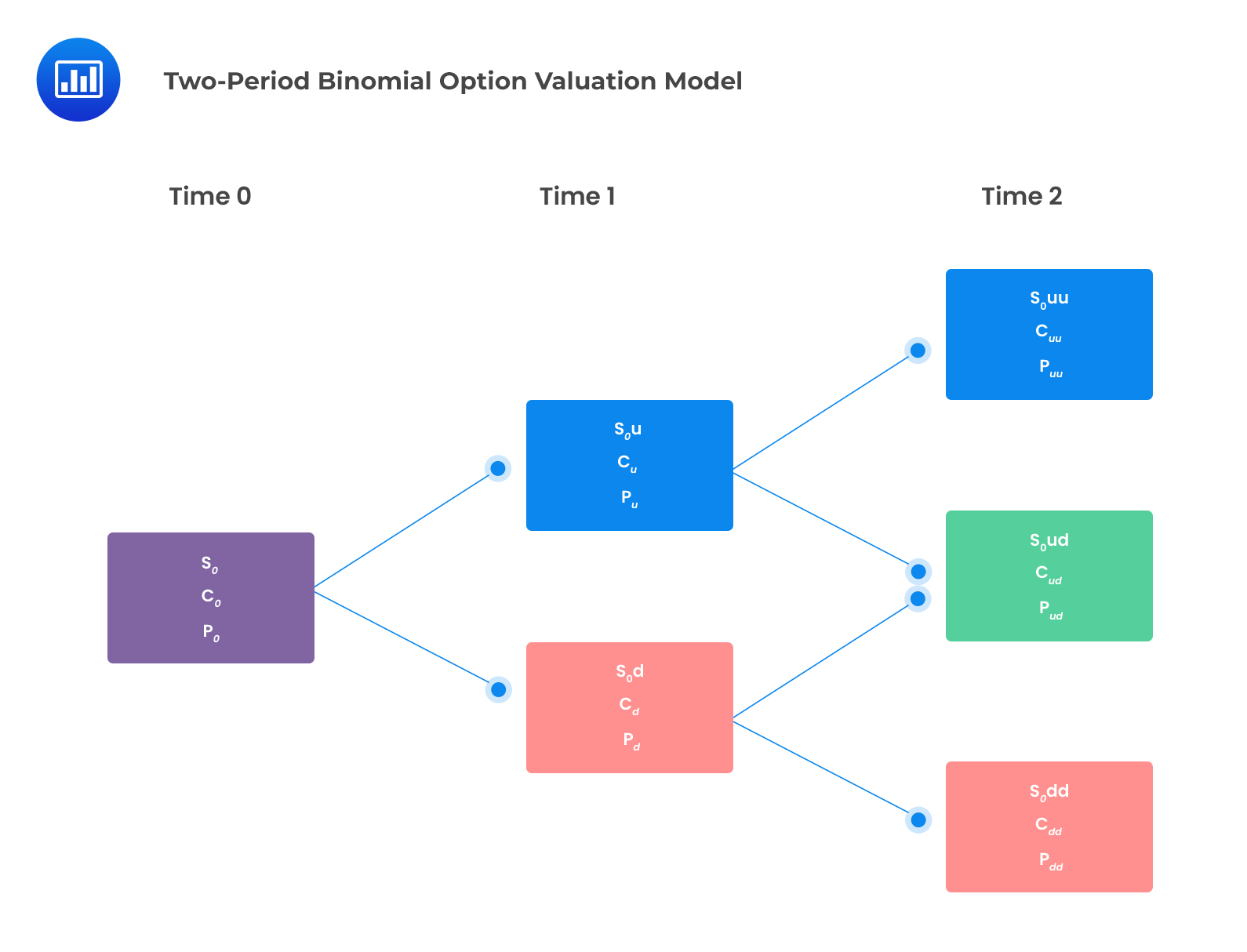 The underlying asset can result in only three possible values:
The underlying asset can result in only three possible values:
A call option under the two-period binomial option model will have three possible payoffs at expiry as follows:
$$ \begin{align*} c_{uu} &=max \left(0, S_0u^2-K\right) \\ C_{ud} &=Max\left(0,S_0ud-K\right) \\ c_{dd} & =Max(0,S_0d^2-K) \end{align*} $$
Similar to a call option, a put option will have three possible payoffs:
$$ \begin{align*} p_{uu}& = Max(0,K – S_0u^2) \\ p_{ud}& = Max(0,K – S_0ud) \\ p_{dd} & = Max(0,K – S_0d^2) \end{align*} $$
A European call option’s value can be determined using the two-step binomial valuation model using the following formula.
$$ c_o=\frac{q^2c_{uu} + 2q\left(1-q\right)c_{ud}\ +\left(1 – q\right)^2c_{dd}}{\left(1 + r\right)^2} $$
The two-period European put value is given as:
$$ p_o=\frac{q^2p_{uu} + 2q\left(1-q\right)p_{ud} +\left(1 – q\right)^2p_{dd}}{\left(1 + r\right)^2} $$
These concepts will be explained more with examples in the sections that follow.
Question
A one-year European call option has a strike price of £60. The underlying non-dividend-paying stock is currently trading at £60. Over one year, the stock price can either jump up to £90 or jump down to £50. The annual risk-free interest rate is 4%. Using a one-period binomial option valuation model, the price of the call option is closest to:
- £2.44.
- £9.04.
- £15.64.
Solution
The correct answer is B.
The payoff of a European call option at expiration is given by:
\(c_u=Max\left(0, S_0u-K\right),\) if the price of the underlying jumps up
and
\(c_d=Max{\left(0,S_0d-K\right)},\) if the stock price jumps down
$$ \begin{align*} u &=\frac{90}{60}=1.5 \\ d &=\frac{50}{60}=0.83 \\ c_u &=Max\left(0,90-60\right)=£30 \\ c_d &=Max\left(0,50-60\right)=£0 \end{align*} $$
The value of a call option is then calculated using the formula:
$$ c_0 =\frac{qc_u+\left(1-q\right)c_d}{1+r} $$
Where:
$$ \begin{align*} q &=\frac{1.04-0.83}{1.5-0.83}=0.3134 \\ c_0 &=\frac {0.3134× £30+0.6866×£0}{1.04}=£9.04 \end{align*} $$
Reading 34: Valuation of Contingent Claims
LOS 34 (a) Describe and interpret the binomial option valuation model and its component terms.
Get Ahead on Your Study Prep This Cyber Monday! Save 35% on all CFA® and FRM® Unlimited Packages. Use code CYBERMONDAY at checkout. Offer ends Dec 1st.