Event-driven Strategies: Merger Arbitr ...
Event-driven (E.D.) hedge fund strategies involve the practice of taking positions in corporate... Read More
Valuing a fixed-rate coupon bond with no embedded options using the arbitrage-free lattice and the spot curve leads to the same bond value. This holds because the binomial interest rate tree is arbitrage-free. However, the spot curve will not work for bonds with embedded options.
A three-year bond with no embedded options pays 5% annual coupons. Given the following spot curve, the bond price with a face value of $100 is closest to:
$$ \begin{array}{c|c} \textbf{Term to Maturity} & \textbf{Spot Rate} \\ \hline 1 & 4.00\% \\ \hline 2 & 5.00\% \\ \hline 3 & 6.00\% \end{array} $$
Solution
$$ \begin{align*} PV &=\frac{PMT}{\left(1+S_1\right)^1}+\frac{PMT}{\left(1+S_2\right)^2}+\ldots+\frac{PMT+FV}{\left(1+S_N\right)^N} \\ &=\frac{5}{1.04}+\frac{5}{{1.05}^2}+\frac{105}{{1.06}^3}=$97.50 \end{align*} $$
We can determine the price of the same bond using a binomial interest rate tree with the following forward rates:
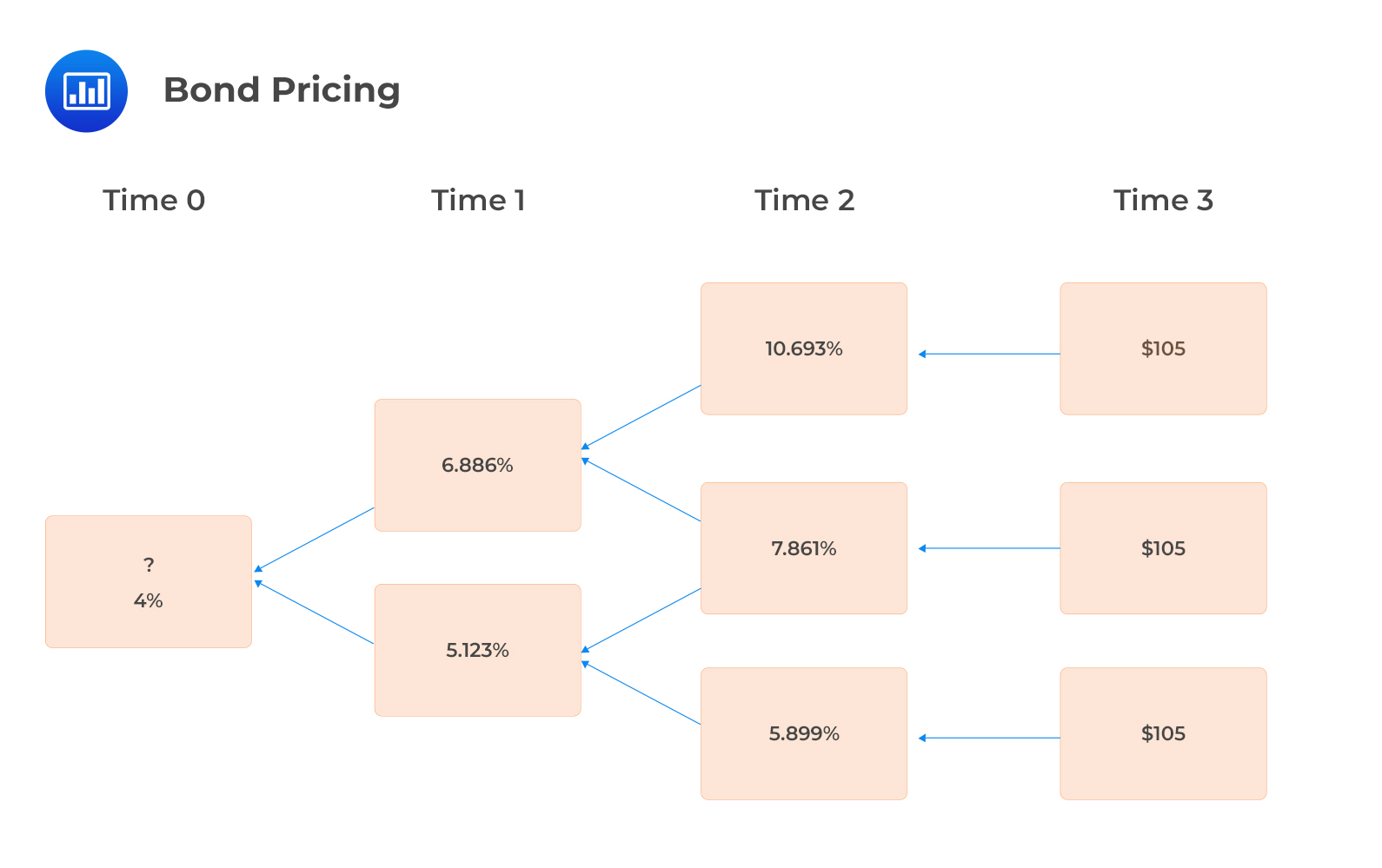 Solution
Solution
$$ \begin{align*} V &=0.5\left[\frac{V_u+C}{1+i}+\frac{V_d+C}{1+i}\right] \\ V_{2,uu} & =\frac{105}{1.10693}=94.857 \\ V_{2,ud} &=\frac{105}{1.07861}=97.348 \\ V_{2,dd} &=\frac{105}{1.05899}=99.151 \\ V_{1,u} &=0.5\left[\frac{94.857+5}{1.06886}+\frac{97.348+5}{1.06886}\right]=94.589 \\ V_{1,d} &=0.5\left[\frac{97.348+5}{1.05123}+\frac{99.151+5}{1.05123}\right]=98.218 \\ V_0&=0.5\left[\frac{94.589+5}{1.04}+\frac{98.218+5}{1.04}\right]=$97.50 \end{align*} $$
We have calibrated the binomial interest rate tree to produce arbitrage-free values consistent with the spot rate curve. This has led to the same option-free bond value of $97.50 as using the spot yield curve.
Question
A fixed-rate coupon bond with no embedded options which is priced using the arbitrage-free binomial lattice leads to a value that’s:
- Higher than that generated using the benchmark spot rate curve.
- Lower than that generated using the benchmark spot rate curve.
- Similar to that generated using the benchmark spot rate curve.
Solution
The correct answer is C.
Valuing a fixed-rate coupon bond with no embedded options using the arbitrage-free lattice and using the spot curve leads to the same bond value. This holds because the binomial interest rate tree is arbitrage-free.
Reading 29: The Arbitrage-Free Valuation Framework
LOS 29 (f) Compare pricing using the zero-coupon yield curve with pricing using an arbitrage-free binomial lattice.
Get Ahead on Your Study Prep This Cyber Monday! Save 35% on all CFA® and FRM® Unlimited Packages. Use code CYBER30 at checkout. Offer ends Dec 1st.