Sampling Error Explained
A student’s t-distribution is a bell-shaped probability distribution symmetrical about its mean. It is regarded as the most suitable distribution to use in the construction of confidence intervals in the following instances:
Apart from being used in the construction of confidence intervals, a t-distribution is used to test the following:
In the absence of explicit normality of a given distribution, a t-distribution may still be appropriate for use if the sample size is large enough for the central limit theorem to be applied. In such a case, the distribution is considered approximately normal.
A t-statistic, also called the t-score, is given by:
$$ t = \cfrac {(x – \mu)}{\left(\cfrac {S}{\sqrt n} \right)} $$
Where:
\(x\) = Sample mean.
\(μ\) = Population mean.
\(S\) = Sample standard deviation.
\(n\) = Sample size.
Relationship between the t-distribution and the Normal Distribution
A t-distribution allows us to analyze distributions that are not perfectly normal. A t-distribution has thicker tails relative to a normal distribution.
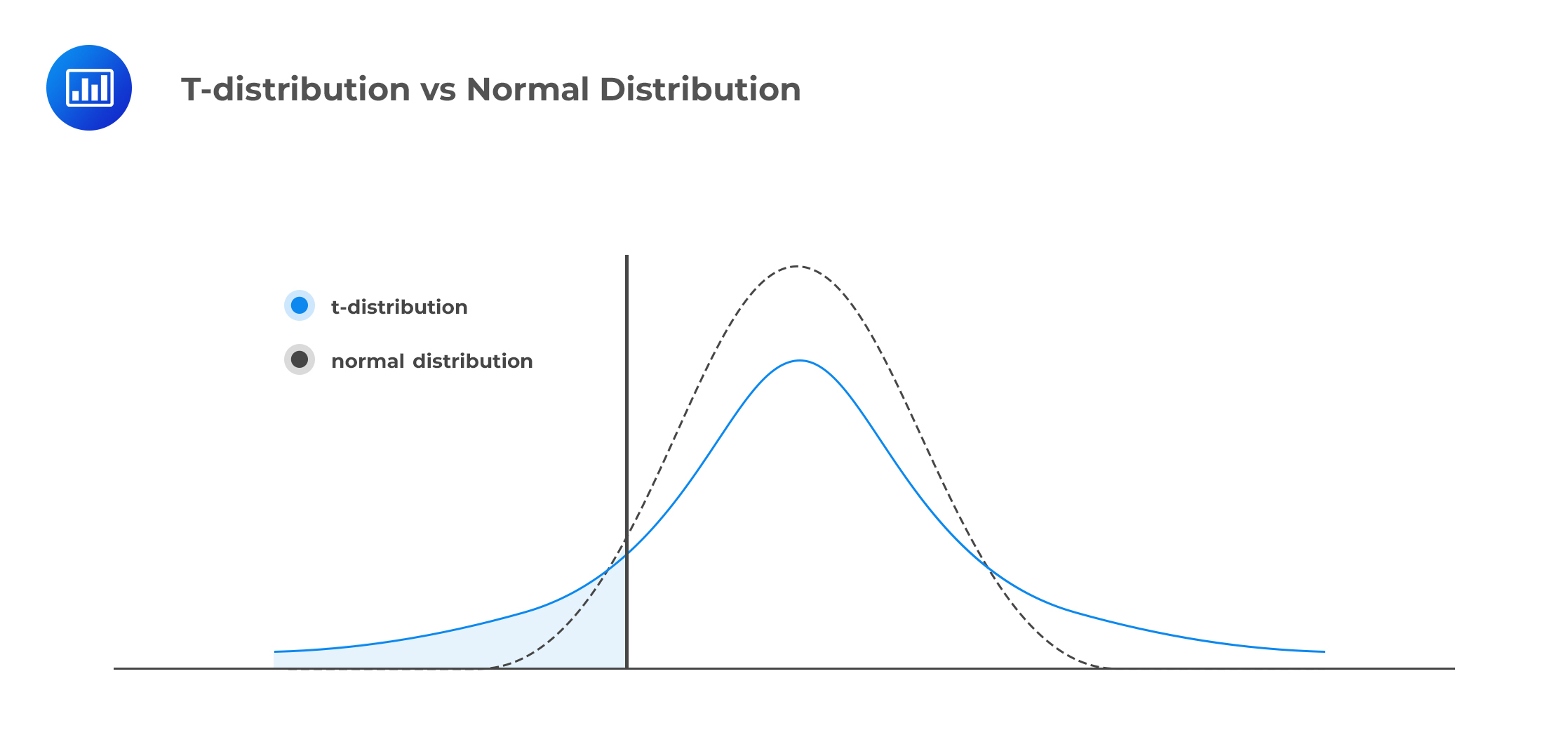
The shape of a t-distribution is dependent on the number of degrees of freedom. It, therefore, follows that as the number of d.f. increases, the distribution becomes more ‘spiked,’ and its tails become thinner, closer to those of the normal distribution.
The t-distribution has the following properties:
A t-distribution, just like several other distributions, has only one parameter: The degrees of freedom (d.f.). The number of degrees of freedom refers to the number of independent observations (total number of observations less 1):
$$ v = n-1 $$
Hence, a sample of 10 observations or elements would be analyzed using a t-distribution with 9 degrees of freedom. Similarly, a 6 d.f. distribution would be used for a sample size of 7 observations.
It is the standard practice for statisticians to use \(t_α\) to represent the t-score with a cumulative probability of \((1 – α)\). Therefore, if we were interested in a t-score with a 0.9 cumulative probability, α would be equal to 1 – 0.9 = 0.1. We would denote the statistic as \(t_0.1\).
However, the value of \(t_α\) depends on the number of degrees of freedom and is often written as \(t_{α,n-1}\). For example, we could write \(t_{0.05,2}= 2.92\) where the second subscript (2) represents the number of d.f.
Just like the normal distribution, the t-distribution is symmetrical about the mean. As such,
$$ t_{\alpha}= -t_{1 – \alpha} \text{ and } t_{1 – \alpha} = -t_{\alpha} $$
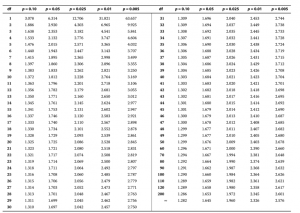
The table below represents one-tailed confidence intervals and various probabilities for a range of degrees of freedom.
Question
Which of the following statements regarding a t-distribution is most likely correct?
- A t distribution is less spread out than a standard normal distribution.
- A t-distribution is symmetric about zero.
- As the degrees-of-freedom increase, a t-distribution becomes wider and flat.
Solution
The correct answer is B.
A t-distribution is a symmetrical, bell-shaped distribution that looks like a normal distribution and has a mean of zero.
A is incorrect. A t-distribution is more spread out than a standard normal distribution.
C is incorrect. As the degrees-of-freedom increase, a t-distribution becomes narrower, taller, and approaches a standard normal distribution.
Get Ahead on Your Study Prep This Cyber Monday! Save 35% on all CFA® and FRM® Unlimited Packages. Use code CYBERMONDAY at checkout. Offer ends Dec 1st.