Tests of Independence
Parametric versus Non-parametric Tests of Independence A parametric test is a hypothesis test... Read More
A test statistic is a standardized value computed from sample information when testing hypotheses. It compares the given data with what an analyst would expect under a null hypothesis. As such, it is a major determinant of the decision to either accept or reject H0, the null hypothesis.
We use test statistic to gauge the degree of agreement between sample data and the null hypothesis. Analysts use the following formula when calculating the test statistic.
$$ \text{Test statistic} = \cfrac { (\text{Sample statistic} – \text{Hypothesized value})}{\text{Standard error of the sample statistic}} $$
The test statistic is a random variable that changes from one sample to another. The following table gives a brief outline of the various test statistics used regularly, based on the distribution the data presumably follows:
$$
\begin{array}{c|c}
\textbf{Hypothesis Test} & \textbf{Test statistic} \\ \hline
\text{Z-test} & \text{Z-statistic (normal distribution)} \\ \hline
\text{Chi-square test} & \text{Chi-square statistic} \\ \hline
\text{t-test} & \text{t-statistic} \\ \hline
\text{ANOVA} & \text{F-statistic} \\
\end{array}
$$
We can subdivide the set of values that the test statistic can take into two regions: The non-rejection region, which is consistent with the H0, and the rejection region (critical region), which is inconsistent with the H0. If the test statistic has a value found within the critical region, we reject the H0.
As is the case with any other statistic, the distribution of the test statistic must be completely specified under the H0 when the H0 is true.
The following is the list of test statistics and their distributions:
$$\begin{array} {c|c|c|c} {}&{}&\textbf{Test Statistic}&\textbf{Number of Degrees of}\\ \textbf{Test Subject}&\textbf{Test Statistic Formula}&\textbf{Distribution}&\textbf{Freedom}\\ \hline \text{Single mean }&t=\frac{\bar{X}-\mu_{0}}{\frac{s }{\sqrt{n}}}&\text{t-distribution}&n-1\\ \hline \text{Difference in means}&t=\frac{\left(\bar{X}_{1}-\bar{X}_{2}\right)-\left(\mu_{1}-\mu_{2}\right)}{\sqrt{\frac{s_{p}^{2}}{n_{1}}+\frac{s_{p}^{2}}{n_{2}}}}&\text{t-Distribution}&n_1+n_2-2\\ \hline \text{Mean of differences}&t=\frac{\bar{d}-\mu_{d 0}}{s_{\bar{d}}}&\text{t-Distribution}&n-1\\ \hline \text{Single variance}&\chi^{2}=\frac{s^{2}(n-1)}{\sigma_{0}^{2}}&\text{Chi-square distribution}&n-1\\ \hline \text{Differences in variances}&F=\frac{s_{1}^{2}}{s_{2}^{2}} &\text{F-distribution}&n_1-1, n_2-1\\ \hline \text{Correlation}&t=\frac{r \sqrt{n-2}}{\sqrt{1-r^{2}}}&\text{t-Distribution}&n-2\\ \hline \text{Independence (categorical data)}&\chi^{2}=\sum_{i=1}^{m} \frac{\left(O_{i j}-E_{i j}\right)^{2}}{E_{i j}}& \text{Chi-square distribution}&(r-1)(c-1)\\ \end{array}$$
Where:
\(\mu_o, \mu_{d_0}\) and \(\sigma^2_0\) denote hypothesized values of the mean, mean difference, and variance, in that order.
\(\bar{x}, \bar{d}, s^2, s\) and \(r\) denote sample mean of the differences, sample variance, sample standard deviation, and correlation, in that order.
\(O_{ij}\) and \(E_ij\) are observed and expected frequencies, respectively, with r indicating the number of rows and c indicating the number of columns in the contingency table.
While using sample statistics to draw conclusions about the parameters of an entire population, there is always the possibility that the sample collected does not accurately represent the population. Consequently, statistical tests carried out using such sample data may yield incorrect results that may lead to erroneous rejection (or lack thereof) of the null hypothesis. This brings us to the two errors highlighted below.
Type I error occurs when we reject a true null hypothesis. For example, a type I error would manifest in the rejection of H0 = 0 when it is actually zero.
Type II error occurs when we fail to reject a false null hypothesis. In such a scenario, the evidence the test provides is insufficient and, as such, cannot justify the rejection of the null hypothesis when it is actually false.
The level of significance, denoted by α, represents the probability of making a type I error, i.e., rejecting the null hypothesis when it is actually true. Consequently, β, the direct opposite of α, is the probability of making a type II error within the bounds of statistical testing. The ideal but practically impossible statistical test would be one that simultaneously minimizes α and β. We use α to determine critical values that subdivide a distribution into the rejection and the non-rejection regions. The figure below gives an example of the critical regions under a two-tailed normal distribution and 5% significance level:
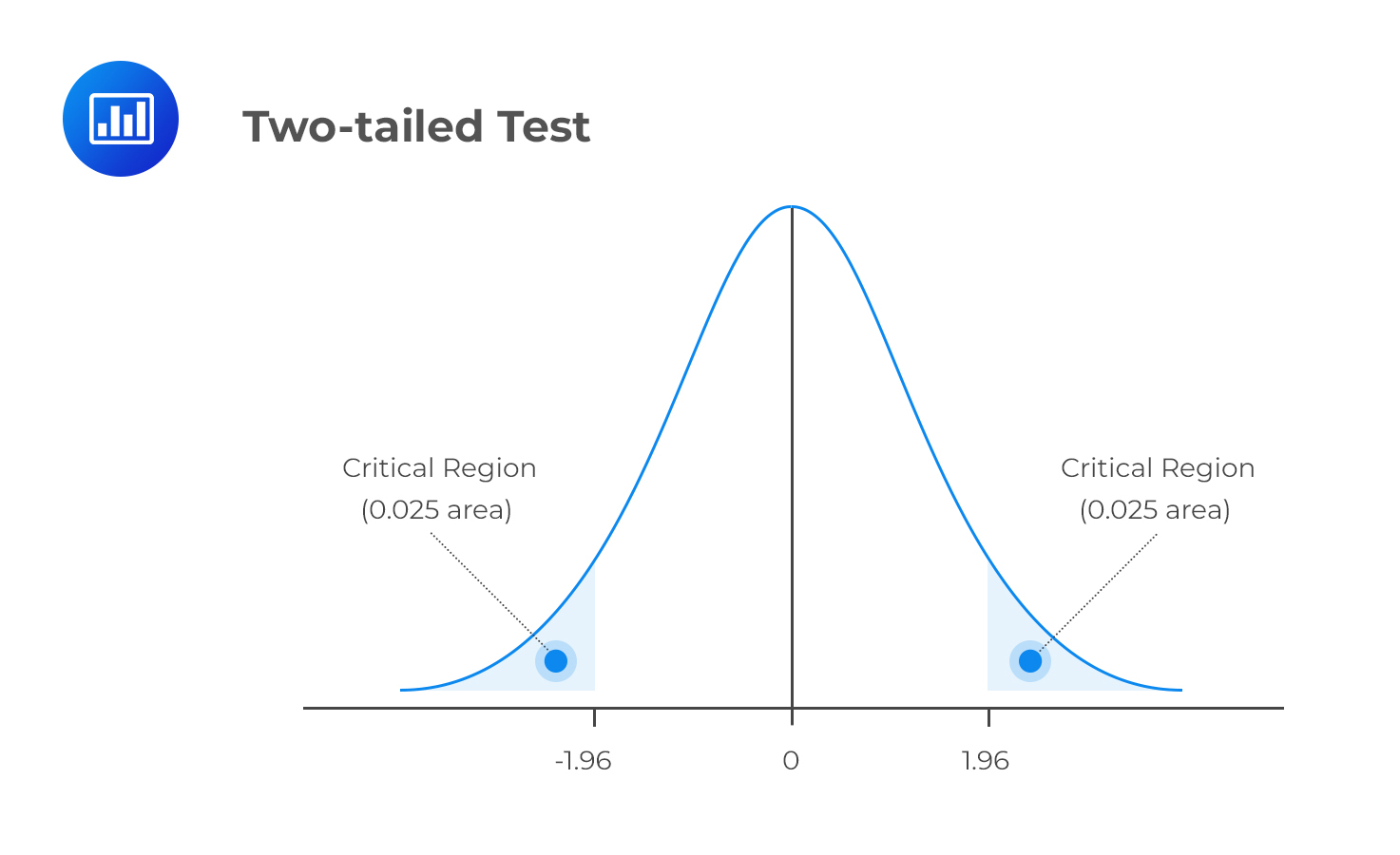
The power of a test is the direct opposite of the level of significance. While the level of significance gives us the probability of rejecting the null hypothesis when it is, in fact, true, the power of a test gives us the probability of correctly discrediting and rejecting the null hypothesis when it is false. In other words, it gives the likelihood of rejecting \(H_0\) when, indeed, it is false. Expressed mathematically,
$$\text{Power of a test = 1- β = 1-P(type II error)}$$
When presented with a situation where there are multiple test results for the same purpose, it is the test with the highest power is considered the best.