Normal Distribution and Confidence Int ...
A confidence interval (CI) gives an “interval estimate” of an unknown population parameter,... Read More
Simple Random Sampling
Simple random sampling, also called chance selection, refers to a method of sample collection in which each element in the population is given an equal chance of being included in the sample. In other words, all the elements in the population have equal probabilities of being chosen. The method assumes that if the population is sufficiently large and the sample is chosen purely on a random basis, the sample is likely to represent all the groups in the population.
Example: Simple Random Sampling
Assume that we want to come up with a sample of 50 CFA Level 1 candidates, given that there are 5000 Level 1 candidates in total.
One approach may involve numbering each of the 5000 candidates, placing the numbers in a basket and shaking the basket to jumble them up. Next, we would randomly draw 50 numbers from the basket, one after the other, without replacement.
A more scientific approach may also involve the use of random numbers where all the 5000 candidates are numbered in a sequence (from 1 to 5000). We may then use a computer to randomly generate 50 numbers between 1 and 5000, where a given number represents a particular candidate who can be identified by their name or admission number.
The underlying feature in random sampling is that each element in the population must have equal chances of being chosen. buy xanax com https://urbanyogaphx.com/ alprazolam tablet buy online
Sampling Distribution
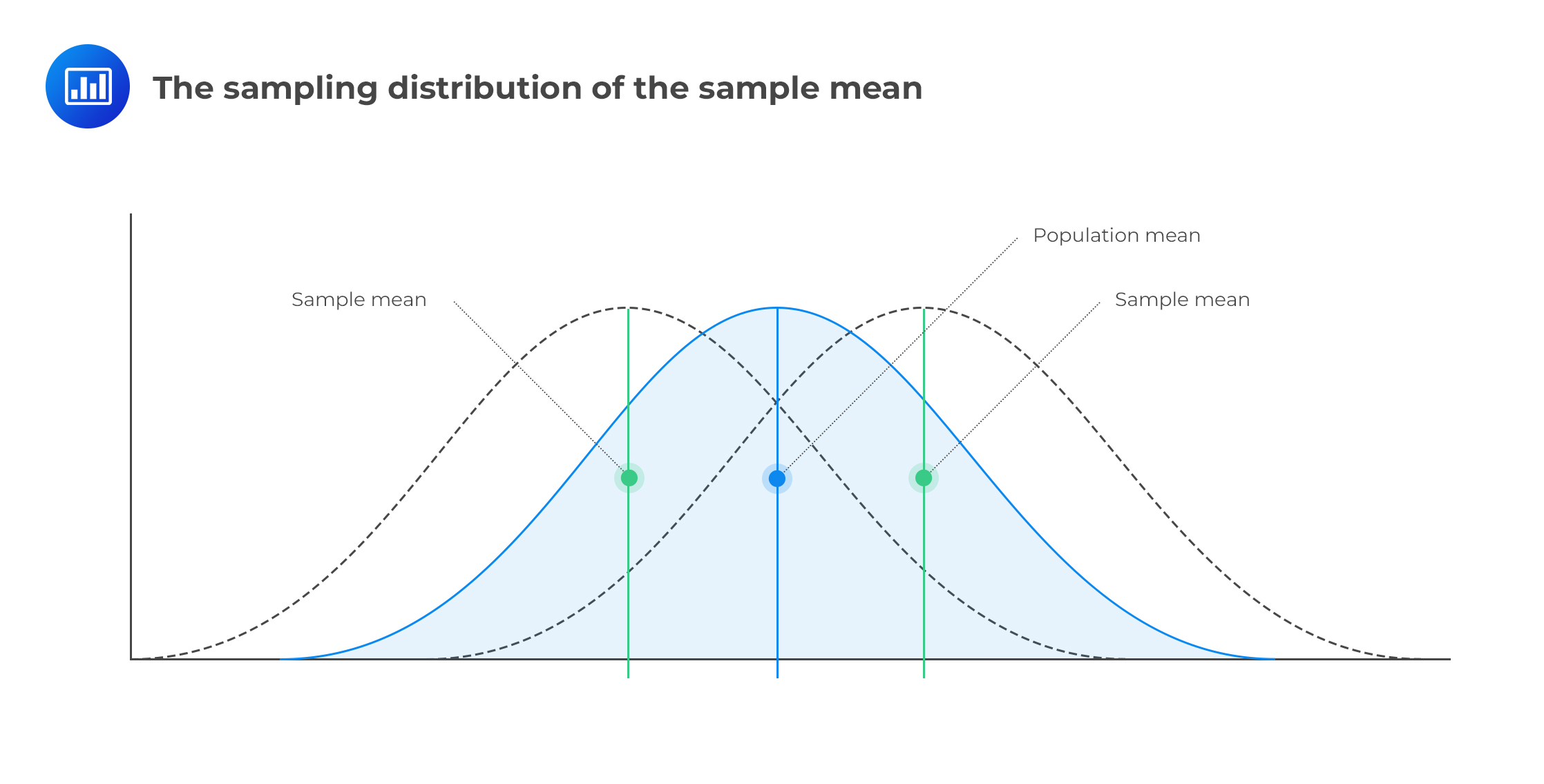
Sampling distribution refers to the distribution of possible outcomes of a sample statistic, such as the mean that would be derived from equally-sized samples drawn from the same population. It’s a probability distribution of a sample statistic from multiple samples.
Example: Sampling Distribution
If we wish to estimate the mean return on 1000 different stocks in a country, we could select a sample of 50 stocks and analyze their financial results to calculate the sample mean return. Suppose we repeatedly selected equally-sized samples from the population, we would end up with several different estimates of the unknown population mean return. The distribution of these sample means would effectively give us the sampling distribution of the mean.
One condition stands: the different samples should be equally-sized and drawn from the same population. This would ensure that the results are reliable and relevant.
Sergio Torrico
2021-07-23
Excelente para el FRM 2
Escribo esta revisión en español para los hispanohablantes, soy de Bolivia, y utilicé
AnalystPrep para dudas y consultas sobre mi preparación para el FRM nivel 2 (lo tomé una sola vez y aprobé muy bien), siempre tuve un soporte claro, directo y rápido, el material sale rápido cuando hay cambios en el temario de GARP, y los ejercicios y exámenes son muy útiles para practicar.
diana
2021-07-17
So helpful. I have been using the videos to prepare for the CFA Level II exam. The videos signpost the reading contents, explain the concepts and provide additional context for specific concepts.
The fun light-hearted analogies are also a welcome break to some very dry content.
I usually watch the videos before going into more in-depth reading and they are a good way to avoid being overwhelmed by the sheer volume of content when you look at the readings.
Kriti Dhawan
2021-07-16
A great curriculum provider. James sir explains the concept so well that rather than memorising it, you tend to intuitively understand and absorb them.
Thank you ! Grateful I saw this at the right time for my CFA prep.
nikhil kumar
2021-06-28
Very well explained and gives a great insight about topics in a very short time. Glad to have found Professor Forjan's lectures.
Marwan
2021-06-22
Great support throughout the course by the team, did not feel neglected
Benjamin anonymous
2021-05-10
I loved using AnalystPrep for FRM.
QBank is huge, videos are great.
Would recommend to a friend
Daniel Glyn
2021-03-24
I have finished my FRM1 thanks to AnalystPrep. And now using AnalystPrep for my FRM2 preparation. Professor Forjan is brilliant. He gives such good explanations and analogies. And more than anything makes learning fun. A big thank you to Analystprep and Professor Forjan. 5 stars all the way!
michael walshe
2021-03-18
Professor James' videos are excellent for understanding the underlying theories behind financial engineering / financial analysis. The AnalystPrep videos were better than any of the others that I searched through on YouTube for providing a clear explanation of some concepts, such as Portfolio theory, CAPM, and Arbitrage Pricing theory. Watching these cleared up many of the unclarities I had in my head. Highly recommended.