The Central Limit Theorem
The central limit theorem asserts that when we have simple random samples each... Read More
Skewness refers to the degree of deviation from a symmetrical distribution, such as the normal distribution. A symmetrical distribution has identical shapes on either side of the mean.
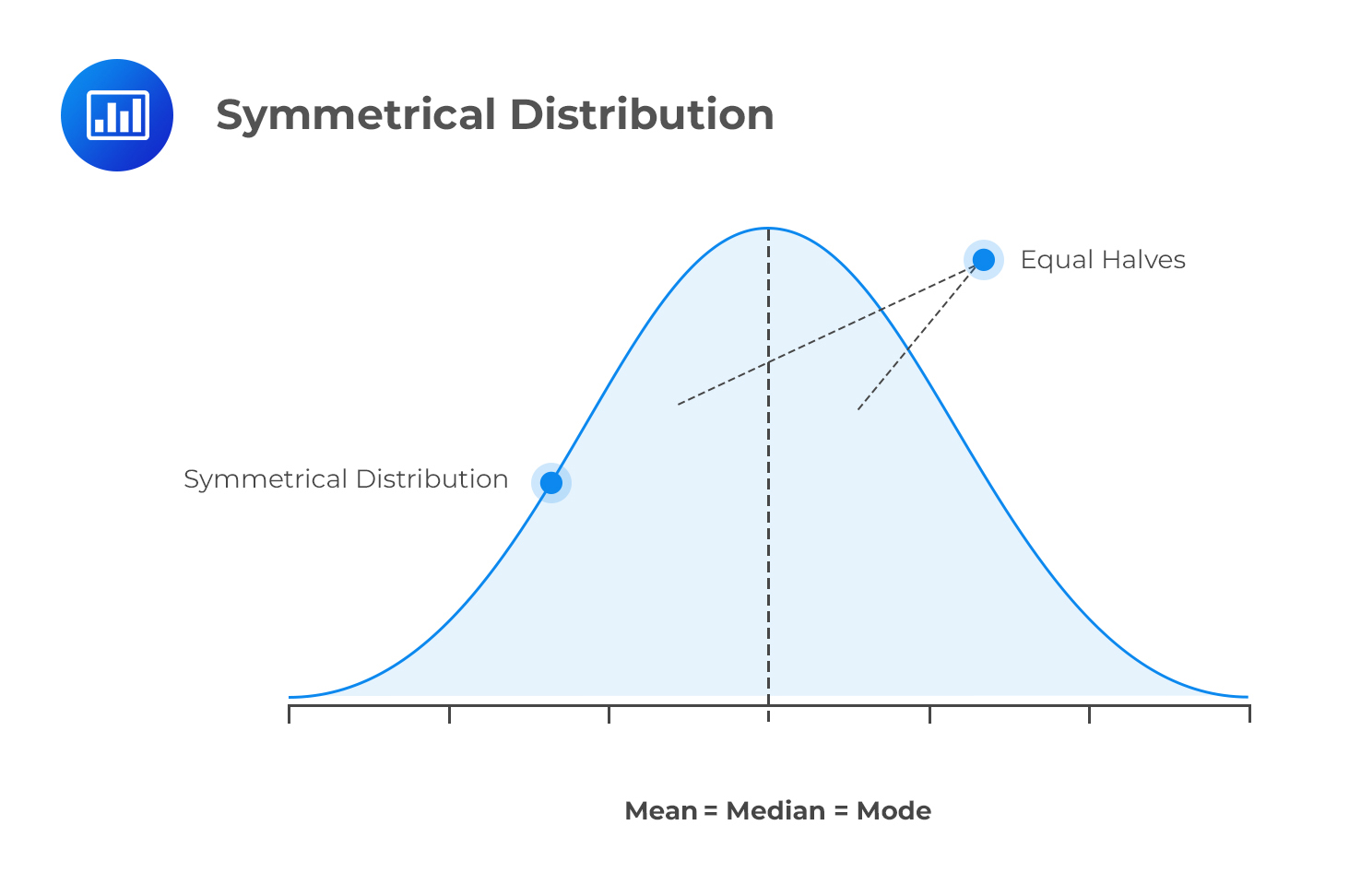
Distributions that are nonsymmetrical have unequal shapes on either side of the mean and lead us to skewness. This is because nonsymmetrical distributions depart from the usual bell shape of the normal distribution.
Skewness can be positive, negative, or in some cases, undefined. The shape of a skewed distribution depends on outliers, which are extremely negative and positive observations.
Positive Skewness
A positively skewed distribution has a long right tail because of many outliers or extreme values on the right side. Perhaps the best way to remember its shape is to consider its points in a positive direction. Most data points are concentrated on the right side.
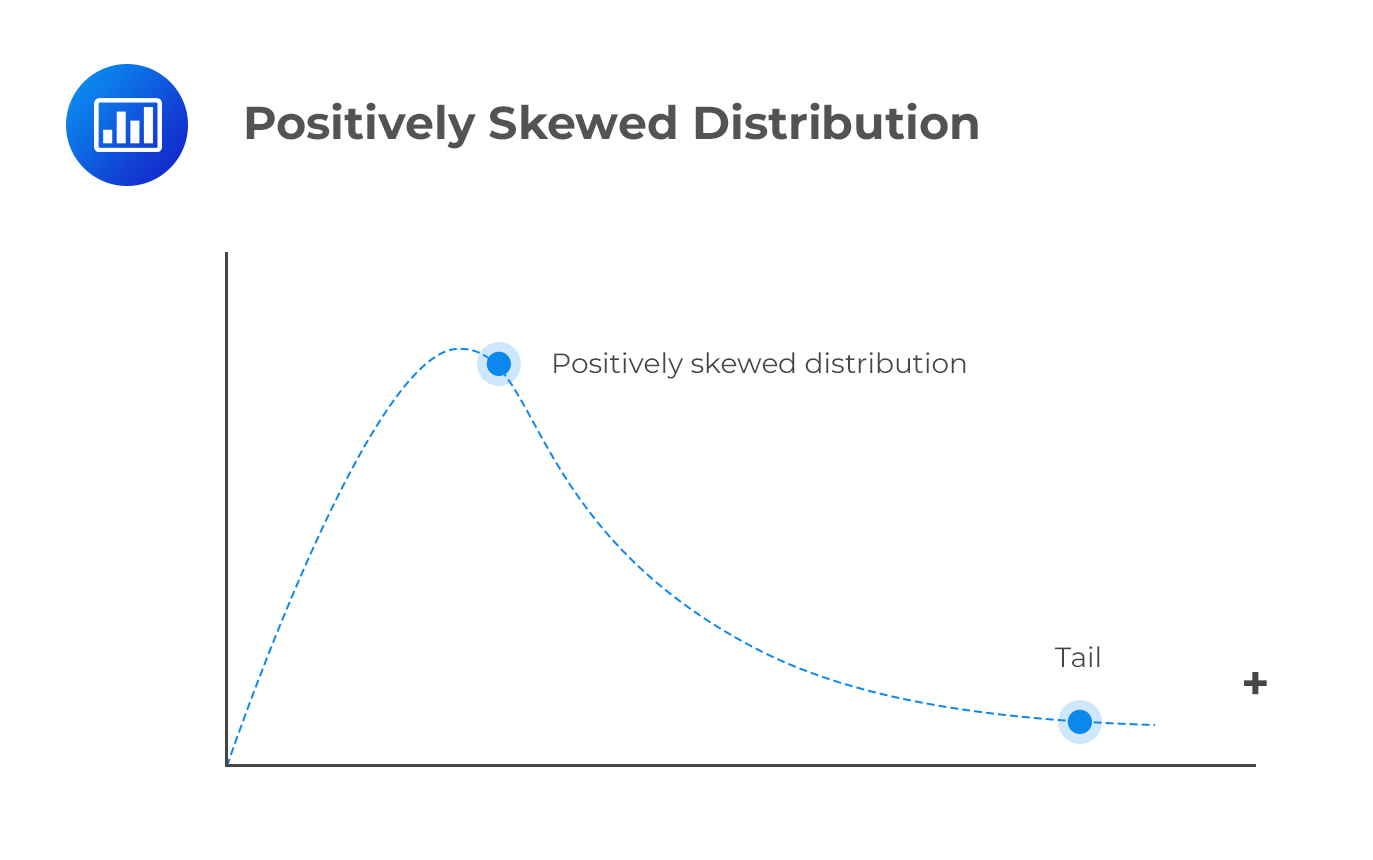
An example of a positively skewed distribution would be the income of individuals living in a certain country.
Negative Skewness
A negatively skewed distribution has a long left tail resulting from many outliers on the left side of the distribution. Therefore, we could say that it points in the negative direction. This is because the left side harbors most of the data points.
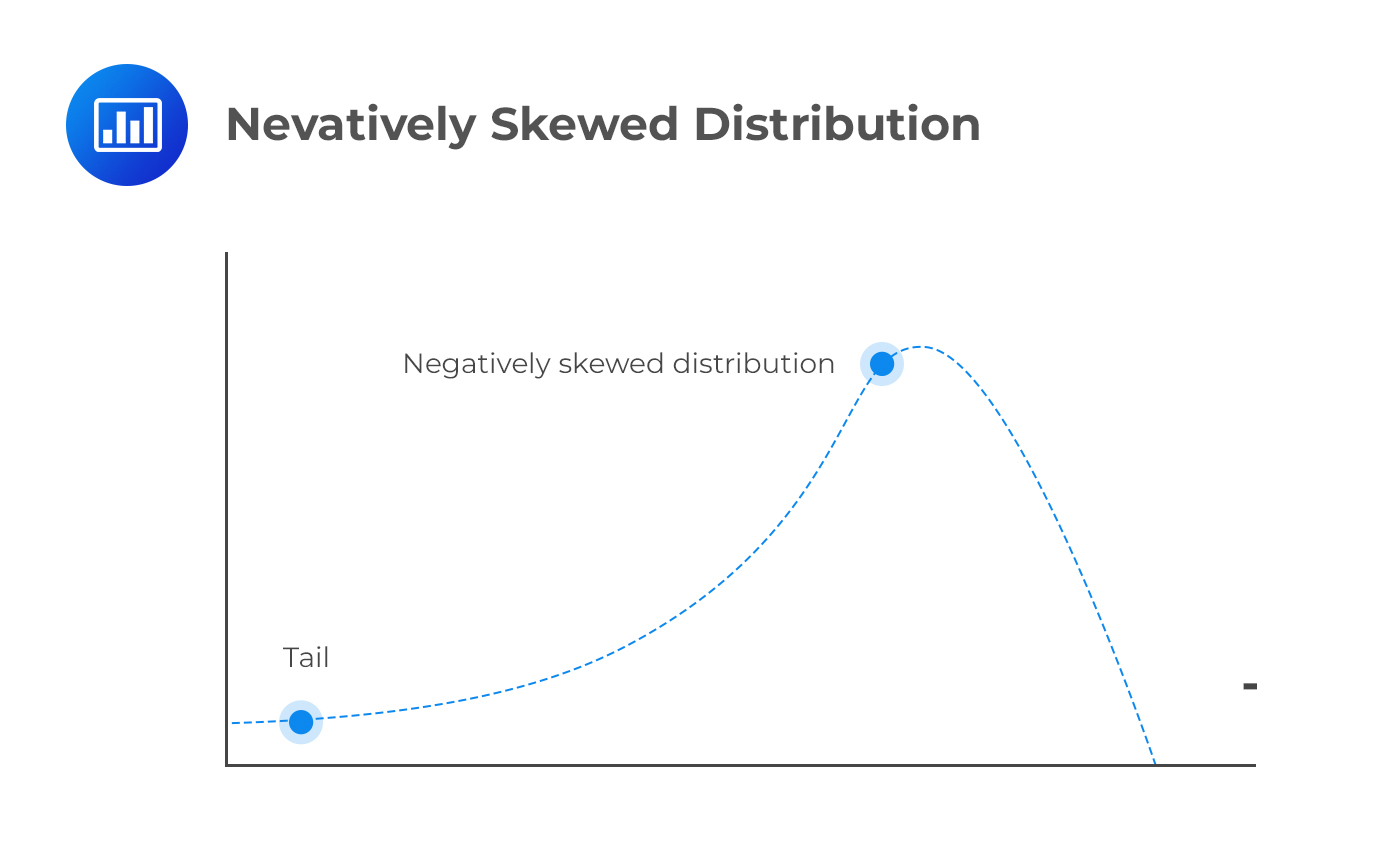
A layman’s example of a negatively skewed distribution would be the number of fingers. Most people have 10 fingers, and only a few have less, possibly after losing some in an accident.
Application of Skewness
Skewness is particularly important in finance. Most market data either exhibit positive skewness or negative skewness, e.g., the prices of stocks and mortgage costs. Thus, an investor can estimate whether the future price will be less or greater than the mean by simply knowing the type of skewness adopted by the particular market segment involved.
Sergio Torrico
2021-07-23
Excelente para el FRM 2
Escribo esta revisión en español para los hispanohablantes, soy de Bolivia, y utilicé
AnalystPrep para dudas y consultas sobre mi preparación para el FRM nivel 2 (lo tomé una sola vez y aprobé muy bien), siempre tuve un soporte claro, directo y rápido, el material sale rápido cuando hay cambios en el temario de GARP, y los ejercicios y exámenes son muy útiles para practicar.
diana
2021-07-17
So helpful. I have been using the videos to prepare for the CFA Level II exam. The videos signpost the reading contents, explain the concepts and provide additional context for specific concepts.
The fun light-hearted analogies are also a welcome break to some very dry content.
I usually watch the videos before going into more in-depth reading and they are a good way to avoid being overwhelmed by the sheer volume of content when you look at the readings.
Kriti Dhawan
2021-07-16
A great curriculum provider. James sir explains the concept so well that rather than memorising it, you tend to intuitively understand and absorb them.
Thank you ! Grateful I saw this at the right time for my CFA prep.
nikhil kumar
2021-06-28
Very well explained and gives a great insight about topics in a very short time. Glad to have found Professor Forjan's lectures.
Marwan
2021-06-22
Great support throughout the course by the team, did not feel neglected
Benjamin anonymous
2021-05-10
I loved using AnalystPrep for FRM.
QBank is huge, videos are great.
Would recommend to a friend
Daniel Glyn
2021-03-24
I have finished my FRM1 thanks to AnalystPrep. And now using AnalystPrep for my FRM2 preparation. Professor Forjan is brilliant. He gives such good explanations and analogies. And more than anything makes learning fun. A big thank you to Analystprep and Professor Forjan. 5 stars all the way!
michael walshe
2021-03-18
Professor James' videos are excellent for understanding the underlying theories behind financial engineering / financial analysis. The AnalystPrep videos were better than any of the others that I searched through on YouTube for providing a clear explanation of some concepts, such as Portfolio theory, CAPM, and Arbitrage Pricing theory. Watching these cleared up many of the unclarities I had in my head. Highly recommended.