Binomial Stock Price Tree
A binomial tree is used to predict stock price movements assuming there are... Read More
Quartiles, quintiles, deciles, and percentiles are values or cut points that partition a finite number of observations into nearly equal-sized subsets. The number of partitions depends on the type of cut point involved.
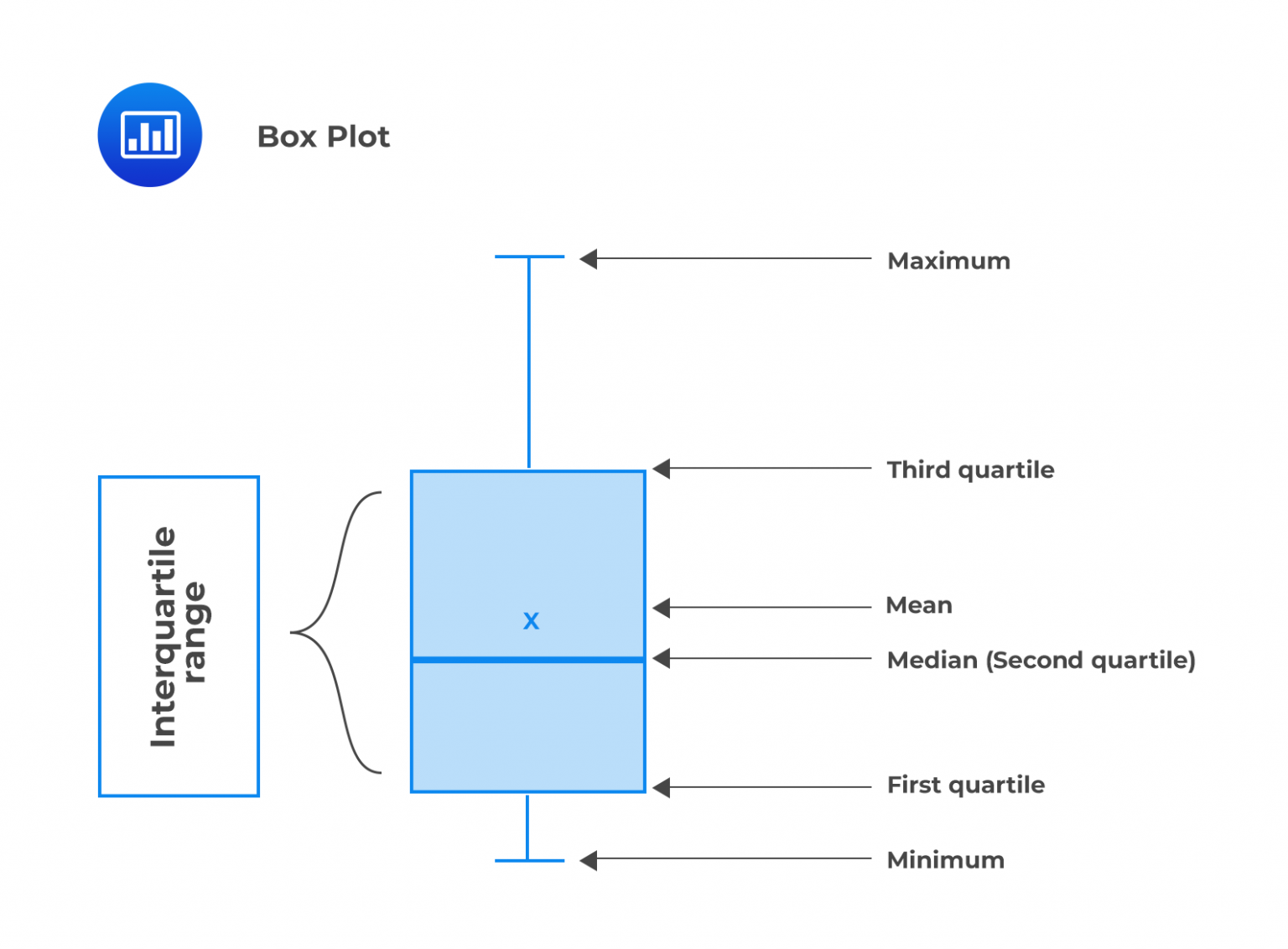
They divide data into four parts. The first quartile, Q1, is referred to as the lower quartile, and the last quartile, Q4, is known as the upper quartile. Q1 splits data into the lower 25% of the values and the upper 75%. Similarly, the upper quartile subdivides data into the lower 75% of the values and the upper 25%. The difference between the upper and lower quartile is known as the interquartile range, which indicates the spread of the middle 50% of the data under review.
Though rarely used in practice, quintiles split a set of data into five equal parts, i.e., fifths. Therefore, the second quintile splits data into the lower 40% of the values and the upper 60%.
The deciles subdivide data into ten equal parts. There are 10 deciles in any data set. For example, the fourth decile splits data into the lower 40% of the values and the upper 60%.
Percentiles split data into 100 equal parts, i.e., hundredths. So, for instance, the 77th percentile splits the data into the lower 77% of the values and the upper 23%.
Financial analysts commonly use the four types of subdivisions to rank investment performance. You should note that quartiles, quintiles, and deciles can all be expressed as percentiles. For instance, the first quartile is just the 25th percentile. Similarly, the fourth decile is simply the 40th percentile. This enables the application of the formula below:
$$ \text{Position of percentile} =\cfrac {(n + 1) y}{100} $$
Where \(n\) is the number of observations and \(y\) is the percentile.
Note: You must always order the data set, usually in ascending order, before calculating any of these values.
Given the following distribution of returns, calculate the lower quartile.
{10% 23% 12% 21% 14% 17% 16% 11% 15% 19%}
Solution
First, we have to arrange the values in ascending order:
{10% 11% 12% 14% 15% 16% 17% 19% 21% 23%}
Next, we establish the position of the first quartile. This is simply the 25th percentile. Therefore:
$$ \begin{align*} P_{25} & =\cfrac {(10 + 1)25}{100} \\ & = 2.75^{\text{th}} \text{ value}\\ \end{align*} $$
Since the value is not straightforward, we have to extrapolate between the 2nd and the 3rd data points. The 25th percentile is three-fourths (0.75) of the way from the 2nd data point (11%) to the 3rd data point (12%):
$$ \begin{align*} & 11\% + 0.75 * (12 – 11) \\ & = 11.75\% \end{align*} $$
Box and whisker plot is used to display the dispersion of data across quartiles. A box and whisker plot consists of a “box” with “whiskers” connected to the box. It shows the following five-number summary of a set of data.
Consider the following box and whisker plot:
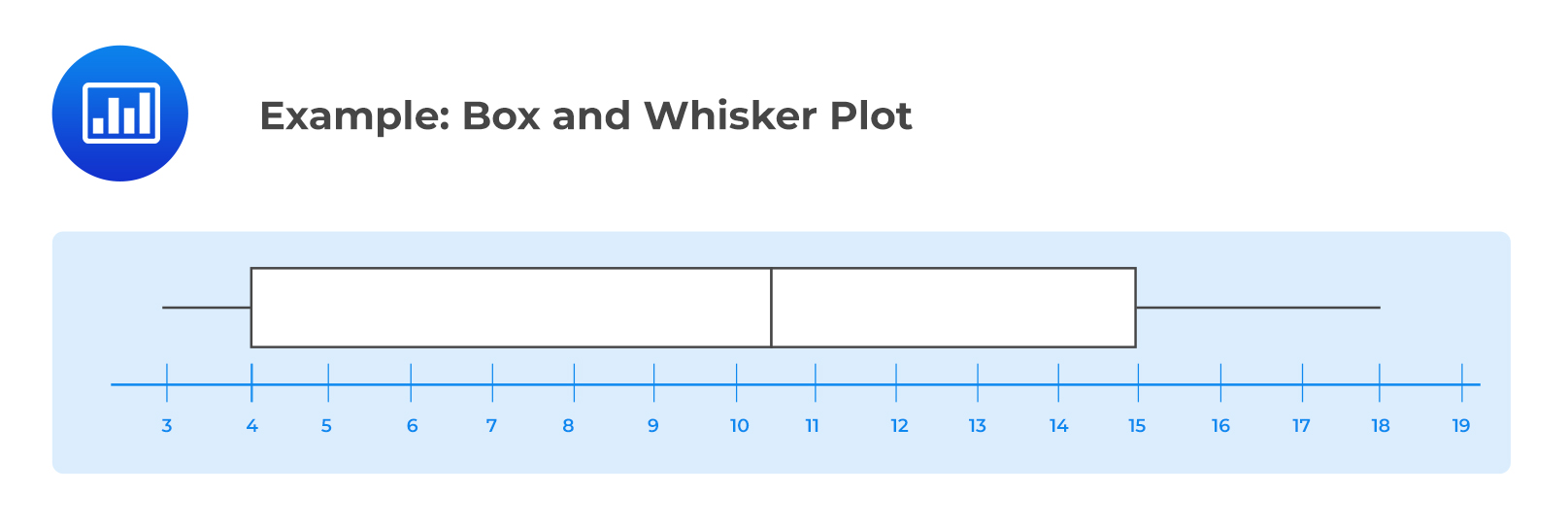
Solutions
Question
A mutual fund achieved the following rates of growth over an 11-month period:
{3% 2% 7% 8% 2% 4% 3% 7.5% 7.2% 2.7% 2.09%}
The 5th decile from the data is closest to:
- 2%.
- 3%.
- 4%.
Solution
The correct answer is B.
First, you should re-arrange the data in ascending order:
{2% 2% 2.09% 2.7% 3% 3% 4% 7% 7.2% 7.5% 8%}
Secondly, you should establish the 5th decile. This is simply the 50th percentile and is actually the median:
$$ \begin{align*} P_{50} & =\frac {(1 + 11) 50}{100} \\ & = 12 \times 0.5 \\ & = 6 \text{ i}.\text{e}. \text{ the }6^{\text{th}} \text{ data point}. \\ \end{align*} $$
Therefore,
$$ \text{the } 5^{\text{th}} \text{ decile} = 50^{\text{th}} \text { percentile} = \text{median} = 3\% $$